A rod is placed along the line,y=2x with its centre at origin. The moment of inertia of the rod is maximum about.
X-axis
Y-axis
Z-axis
Data insufficient
The correct Answer is:C
To find the axis about which the moment of inertia of a rod placed along the line y=2x with its center at the origin is maximum, we can follow these steps:
Step 1: Understand the position of the rod
The rod is placed along the line y=2x. This means that the rod has a slope of 2 and is positioned diagonally in the xy-plane. The center of the rod is at the origin (0,0).
Step 2: Determine the orientation of the rod
The line y=2x can be expressed in vector form. The direction vector of the line can be taken as (1,2). Therefore, the rod can be represented as extending from (−L/2,−L) to (L/2,L), where L is the length of the rod.
Step 3: Moment of Inertia about different axes
The moment of inertia I of a rod about an axis can be calculated using the following formulas:
- For an axis through the center of mass (perpendicular to the length of the rod):
Icm=112ML2
- For an axis through one end of the rod (perpendicular to the length of the rod):
Iend=13ML2
Step 4: Identify maximum moment of inertia
The moment of inertia is maximum when the axis of rotation is perpendicular to the length of the rod. Since the rod is oriented along the line y=2x, the axis that is perpendicular to this line will have a slope that is the negative reciprocal of 2, which is −12.
Step 5: Conclusion
The axis that is perpendicular to the rod and passes through the center of the rod will yield the maximum moment of inertia. This axis can be represented as the z-axis in a 3D coordinate system where the rod lies in the xy-plane.
Thus, the moment of inertia of the rod is maximum about the z-axis.
The rod is placed along the line y=2x. This means that the rod has a slope of 2 and is positioned diagonally in the xy-plane. The center of the rod is at the origin (0,0).
The line y=2x can be expressed in vector form. The direction vector of the line can be taken as (1,2). Therefore, the rod can be represented as extending from (−L/2,−L) to (L/2,L), where L is the length of the rod.
The moment of inertia I of a rod about an axis can be calculated using the following formulas:
- For an axis through the center of mass (perpendicular to the length of the rod):
Icm=112ML2
- For an axis through one end of the rod (perpendicular to the length of the rod):
Iend=13ML2
The moment of inertia is maximum when the axis of rotation is perpendicular to the length of the rod. Since the rod is oriented along the line y=2x, the axis that is perpendicular to this line will have a slope that is the negative reciprocal of 2, which is −12.
The axis that is perpendicular to the rod and passes through the center of the rod will yield the maximum moment of inertia. This axis can be represented as the z-axis in a 3D coordinate system where the rod lies in the xy-plane.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises25videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.315videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.14videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
Similar Questions
An electric dipole is placed along x-axis with its centre at origin:
View SolutionMoment of inertia of a inclined rod.
View SolutionA uniform disc of radius R lies in the x−y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y=x+c. The value of c will be.
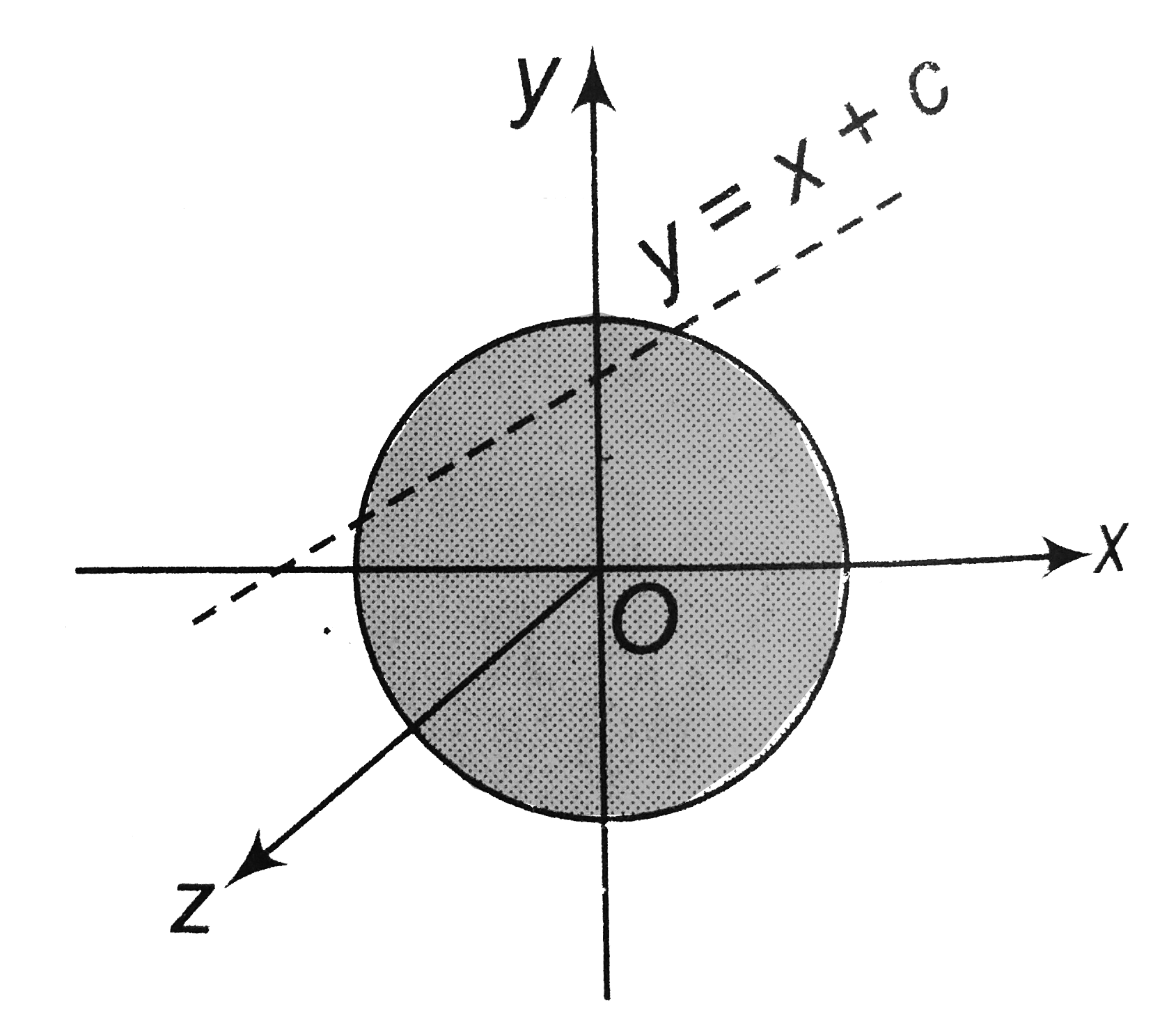 .View Solution
.View SolutionA uniform disc of radius R lies in x-y plane with its centre at origin. Its moment of inertia about the axis x=2R and y=0 is equal to the moment of inertia about the axis y=d and z=0, where d is equal to
View SolutionCalculate the moment of inertia of the given rod about an axis CD.
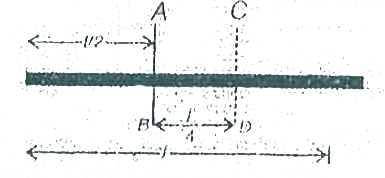 View Solution
View SolutionCalculate the moment of inertia of the given rod about an axis CD
 View Solution
View SolutionTwo rods each of mass m and length 1 are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them, is :
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be
 View Solution
View SolutionA non conducting infinite rod is placed along the z−axis the upper half of the rod (lying along z≥0) is charged positively with a uniform linear charge density +λ, while the lower half (z<0) is charged negatively with a uniform linear charge density −λ. The origin is located at the junction of the positive and negative halves of the rod. A uniformly charged annular disc (surface charge density : σ0) of inner radius R and outer radius 2R is placed in the x−y plane with its centre at the origin. find the force on the rod due to the disc.
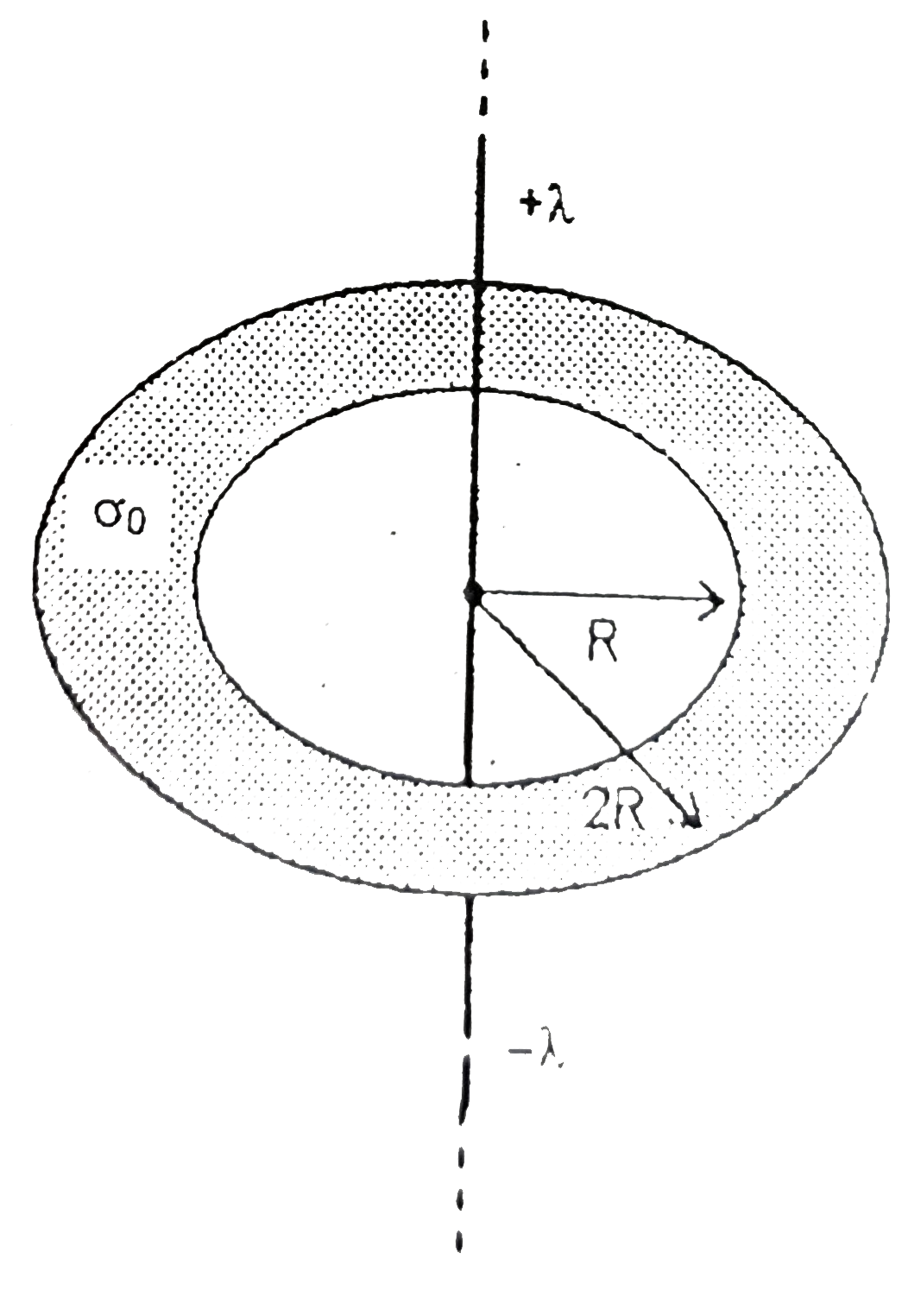 View Solution
View SolutionThree thin rods each of length Land mass M are placed along x, y and z-axes such that one end of each rod is at origin. The moment of inertia of this system about z-axis is
View Solution

