A rod lies along the x-axis with one end at the origin and the other at x→∞. It carries a uniform charge λ C/m. The electric field at the point x = -a on the axis will be
→E=λ4πε0a(−ˆi)
→E=λ4πε0a(ˆi)
→E=λ2πε0a(−ˆi)
E=λ2πε0a(ˆi)
The correct Answer is:A
The electric field at the point x = -a on the axis will be →E=λ4πε0a(−ˆi)
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - NEET ITALS
1 Videos
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - NEET VITALS
18 Videos
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - AIPMT/NEET (MCQ.s)
34 Videos
- ELECTRONIC DEVICESBOOK - MTG GUIDECHAPTER - ELECTRONIC DEVICESEXERCISE - AIPMT/NEET (MCQs)
42 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - AIPMT/NEET (MCQs)
48 Videos
Similar Questions
A rod lies along the X-axis with one end at the origin and the other at x→∞. It carries a uniform charge λCm−1. The electric field at the point x=−a on the axis will be
View SolutionA rod of length L lies along the x-axis with its left end at the origin. It has a non-uniform charge density λ=αx, where a is a positive constant.
(a) What are the units of α?
(b) Calculate the electric potential at point A where x=−d .
View Solution
Knowledge Check
A rod lies along the X-axis with one end at the origin and the other at x→∞. It carries a uniform charge λCm−1. The electric field at the point x=−a on the axis will be
AE=λ4πε0a(−ˆi)BE=λ4πε0a(ˆi)CE=λ2πε0a(−ˆi)DE=λ2πε0a(ˆi)A positively charged rod lies along X-axis in such a manner that one end of the rod is at the origin and the other end at x=−∞. The linear charge density for the rod is λ. Electric field intensity at x =a is
Aλ4πε0aˆiB−λ4πε0aˆiCλ4πε0a2ˆiD−λ4πε0a2ˆiA rod of length l is placed along x - axis. One of its ends is at the origin. The rod has a non - uniform charge density λ=ax, a being a positive constant. The electric potential at the point P (origin) as shown in the figure is
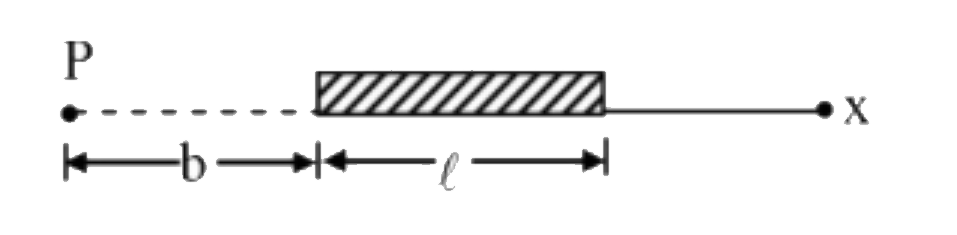 AV=a4πε0(lb(b+l))BV=a4πε0(bl(b+l))CV=a4πε0(bl)DV=a4πε0(lb)
AV=a4πε0(lb(b+l))BV=a4πε0(bl(b+l))CV=a4πε0(bl)DV=a4πε0(lb)
A rod of length L lies along the x-axis with its left end at the origin. It has a non-uniform charge density λ=αx, where a is a positive constant.
(a) What are the units of α?
(b) Calculate the electric potential at point A where x=−d .
View SolutionA continuous line of charge oflength 3d lies along the x-axis, extending from x+d tox+4d . the line carries a uniform linear charge density λ.

In terms of d,λ and any necessary physical constants, find the magnitude of the electric field at the origin:
View SolutionA rod of length l is placed along x - axis. One of its ends is at the origin. The rod has a non - uniform charge density λ=ax, a being a positive constant. The electric potential at the point P (origin) as shown in the figure is

View SolutionA rod of length 'l' is placed along x-axis. One of its ends is at the origin. The rod has a non-uniform charge density λ= a, a being a positive constant. Electric potential at P as shown in the figure is -
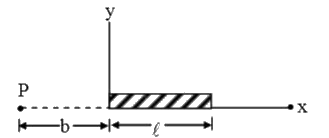
View SolutionA rod of length 'l' is placed along x-axis. One of its ends is at the origin. The rod has a non-uniform charge density λ= a, a being a positive constant. Electric potential at P as shown in the figure is -

View Solution
