A continuous line of charge oflength 3d lies along the x-axis, extending from x+d tox+4d . the line carries a uniform linear charge density λ.

In terms of d,λ and any necessary physical constants, find the magnitude of the electric field at the origin:
λ/5π∈0d
λ/4π∈0d
3λ/16π∈0d
3λ/8π∈0d
Step by step video & image solution for A continuous line of charge oflength 3d lies along the x-axis, extending from x + d to x + 4d . the line carries a uniform linear charge density lambda. In terms of d,lambda and any necessary physical constants, find the magnitude of the electric field at the origin: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Numerical MCQs Single options Correct
64 Videos
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Advance MCQs
40 Videos
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Discussion Question
25 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Advance MCQs
33 Videos
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems
107 Videos
Similar Questions
A continuous line of charge of length 3d lies along the x-axis, extending from x + d to x + 4d, The line carries a uniform linear charge density lambd . In terms of d,λ and any necessary physical constant find the magnitude of the electric field at the origin.
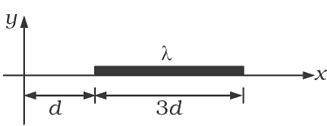
View SolutionFind the electric field at the origin due to the line charge (ABCD) of linear charge density λ,

View Solution
Knowledge Check
Two parallel infinite line charges with linear charge densities +λC/m and −λ C/m are placed at a distance of 2R in free space. What is the electric field mid-way between the two line charges?
Aλ2πε0RN/CBzeroC2λπε0RN/CDλπε0RN/CA rod lies along the x-axis with one end at the origin and the other at x→∞. It carries a uniform charge λ C/m. The electric field at the point x = -a on the axis will be
A→E=λ4πε0a(−ˆi)B→E=λ4πε0a(ˆi)C→E=λ2πε0a(−ˆi)DE=λ2πε0a(ˆi)A rod lies along the X-axis with one end at the origin and the other at x→∞. It carries a uniform charge λCm−1. The electric field at the point x=−a on the axis will be
AE=λ4πε0a(−ˆi)BE=λ4πε0a(ˆi)CE=λ2πε0a(−ˆi)DE=λ2πε0a(ˆi)
A rod of length L lies along the x-axis with its left end at the origin. It has a non-uniform charge density λ=αx, where a is a positive constant.
(a) What are the units of α?
(b) Calculate the electric potential at point A where x=−d .
View SolutionObtain the formula for the electric field due to a along thin wire of uniform linear charge density λ without using Gauss's law.
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density is λ such that λ=a+bx. Find the mass of the rod.
View SolutionA rod of length L is placed along the x-axis between x = 0 and x = L. The linear density (mass/ length) λ of the rod varies with the distance x from the origin as λ=Rx. Here, R is a positive constant. Find the position of centre of mass of this rod.
View SolutionObtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss's law. [Hint. use Coulomb's law directly and evaluate the necessary integral].
View Solution
