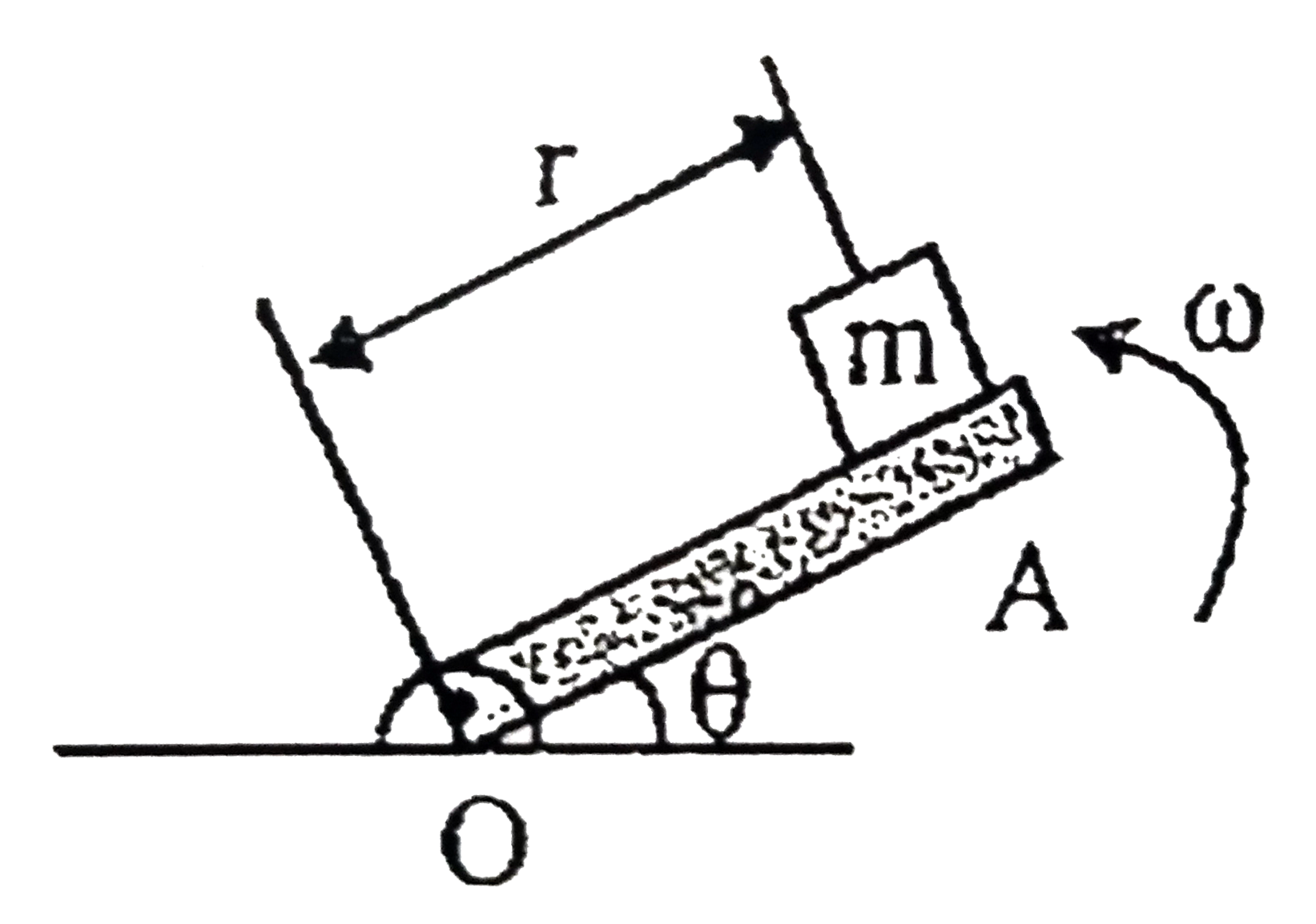
A rod OA rotates about a horizontal axis through O with a constant aniclockwise velocity ω=3reds−1. As it passes the position θ=0, a small block of mass m is placed on it at a radial distance r=450mm if the block is observed to slip at θ=50∘ . Find the coefficient of static friction between the block and the rot
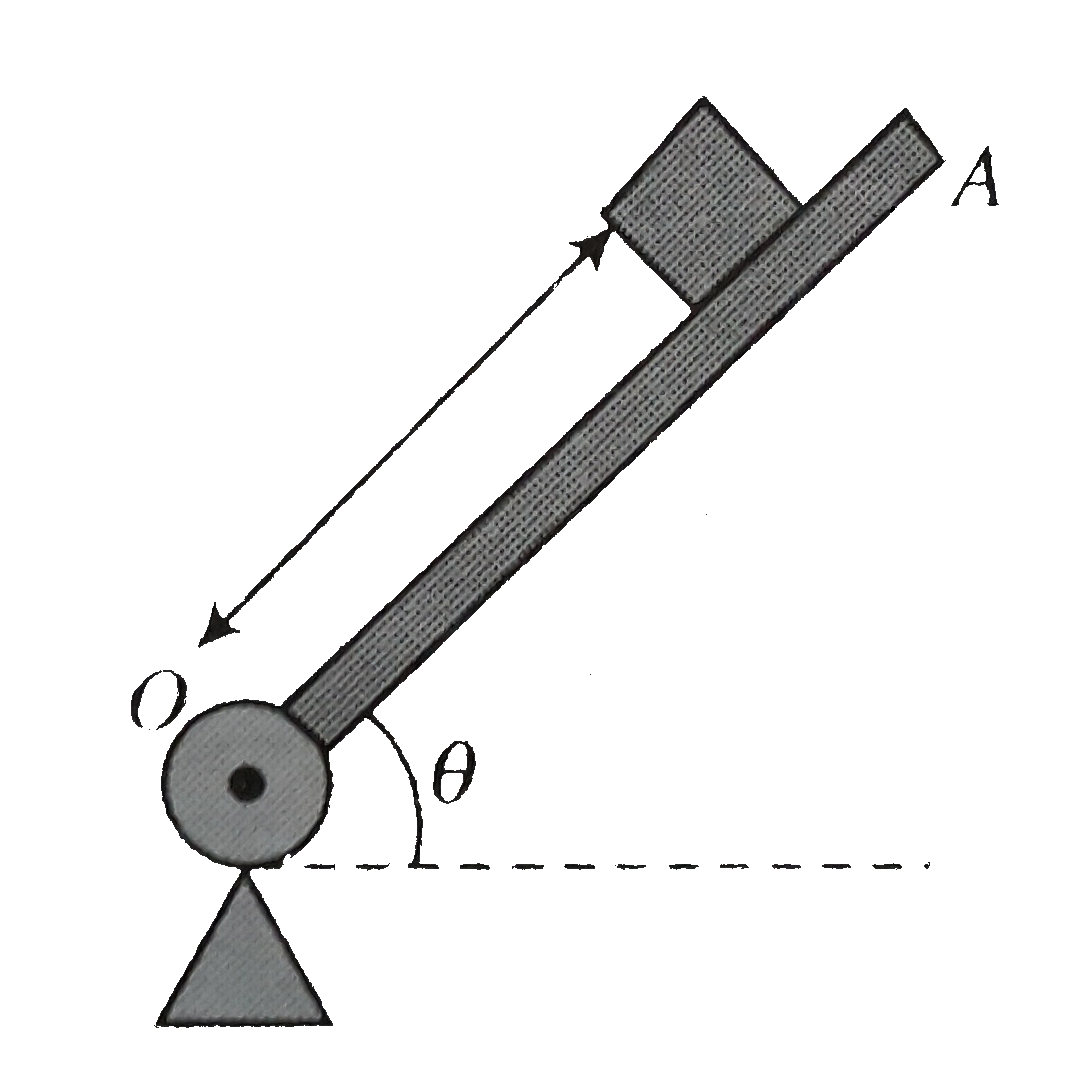
(Given that sin50∘=0.766,cos50∘=0.64)
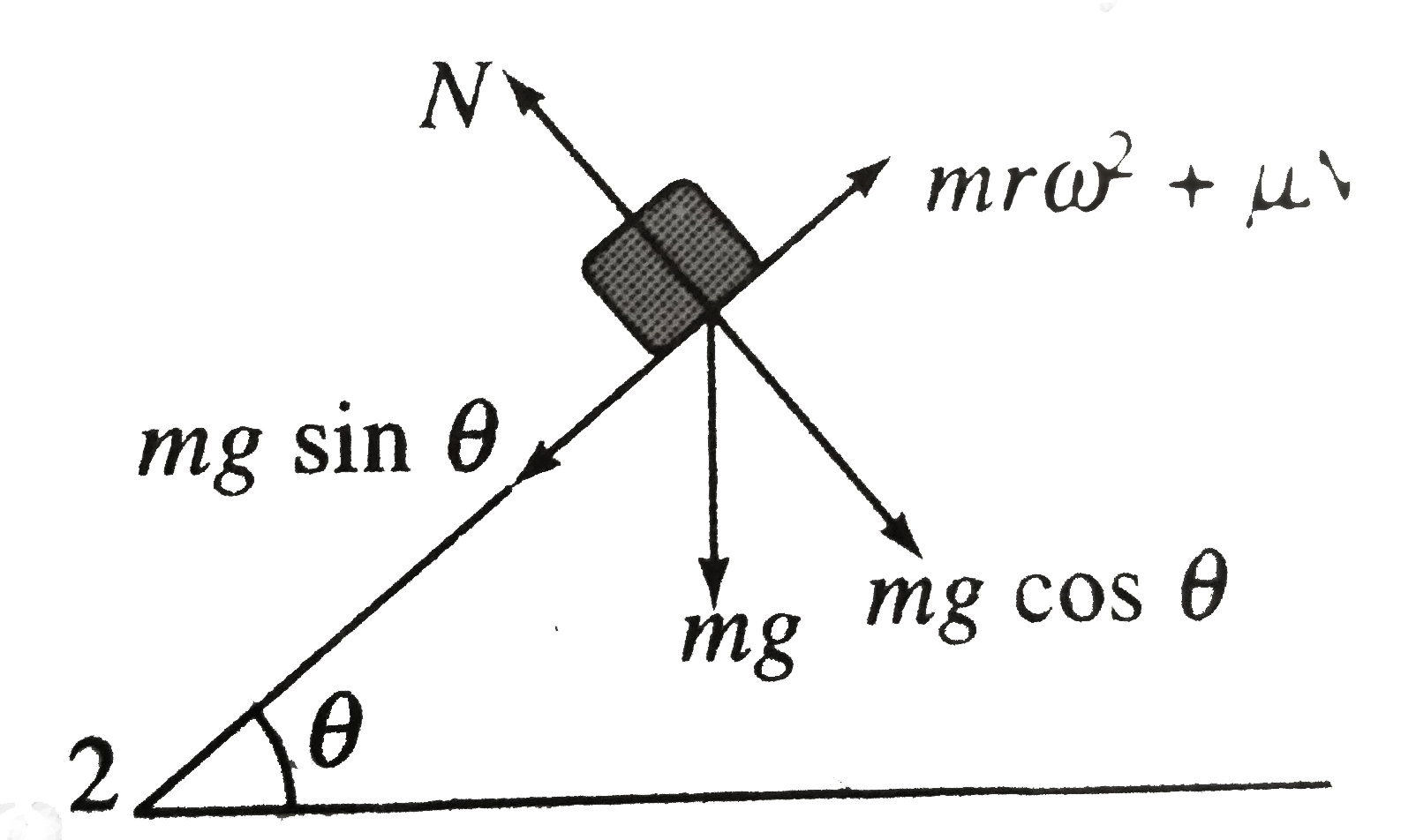
At the time of slipping maximum friction acts on the body in the frame of rod
mgsinθ=μN+mrω2
Also N=mgcosθ
mgsinθ=μmgcosθ+mrω2
Here r=0.45m,θ=50∘
sin50∘=0.766 and cos50∘=0.64
μ=mgsinθ−mrω2mgcosθ=gsinθ−rω2gcosθ=0.56
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective21videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct87videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.216videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
A wooden plank OA rotates in vertical plane about horizontal axis through O with a constant angular velocity ω=3rad/s . As it passes the position θ=0 , a small mass m is placed upon it at a radial distance r=0⋅5 m . If the mass m starts sliding at θ=37∘ , find the coefficient of friction between mass and the plane .
View SolutionA block on table shown in is just on the edge of slipping Find the coefficient of static friction between the blocks and table
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
A rod OA rotates about a horizontal axis through O with a constant anti-clockwise velocity ω=3rad/s. As it pases the positions θ=0∘ a small block of mass m is placed on it at a radial distacne r=450 mm If the block is observed to slip at θ=50∘ the coefficient of static friction bewteen the block and the rod is (Given that ,sin50∘=0766,cos50∘=0.64)
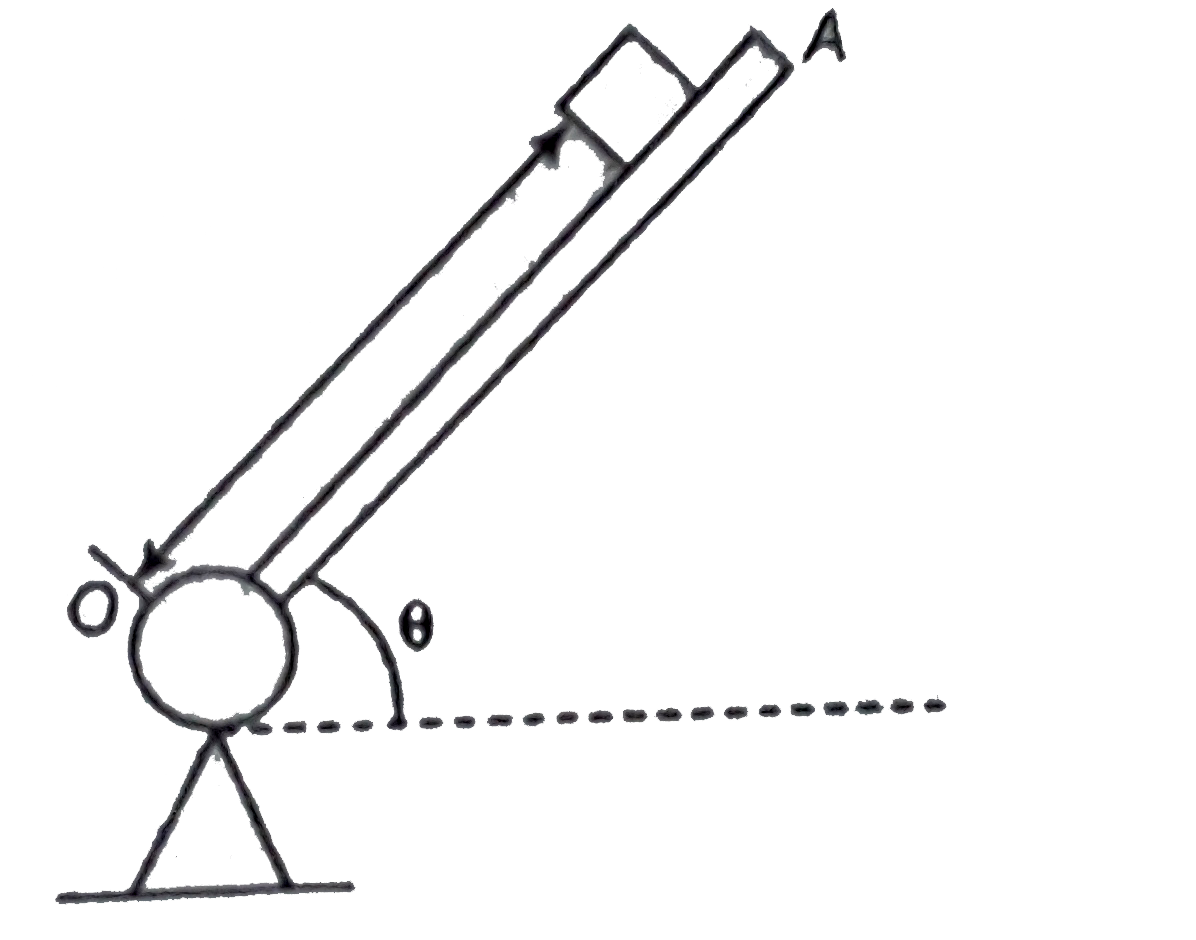 A0.2B0.55C0.8D1
A0.2B0.55C0.8D1 - Question 2 - Select One
A block of mass 1 kg is placed on a truck which accelerates with acceleration 5ms−2. The coefficient of static friction between the block and truck is 0.6. The frictional force acting on the block is
A5 NB6 NC5.82 ND4.6 N - Question 3 - Select One
A block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
AmgBμmgcosθCmgsinθDμmgtanθ
The inclined plane OA rotates in vertical plane about a horizontal axis through O with a constant counter clockwise velocity ω=3 rad/sec. As it passes the position θ=0, a small m=1 kg is placed upon it at a radial distance r=0.5 m. if the mass is observed to be at rest with respect to inclined plane. The value of static friction force at θ=37∘ between the mass and the incline plane
 View Solution
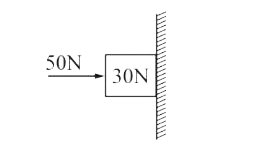
View SolutionA block of weight 30 N is in contact with a rough wall. A force of 50 N is applied as shown in the figure. Find the coefficient of static friction between the wall and the block assuming the block is just about to slip.
 View Solution
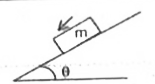
View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.
 View Solution
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA block slides with a velocity of 10 m/s on a rough horizontal surface. It comes to rest after covering a distance of 50 metre. If g is 10m/s2, then the coefficient of dynamic friction between the block and the surface is
View Solution

