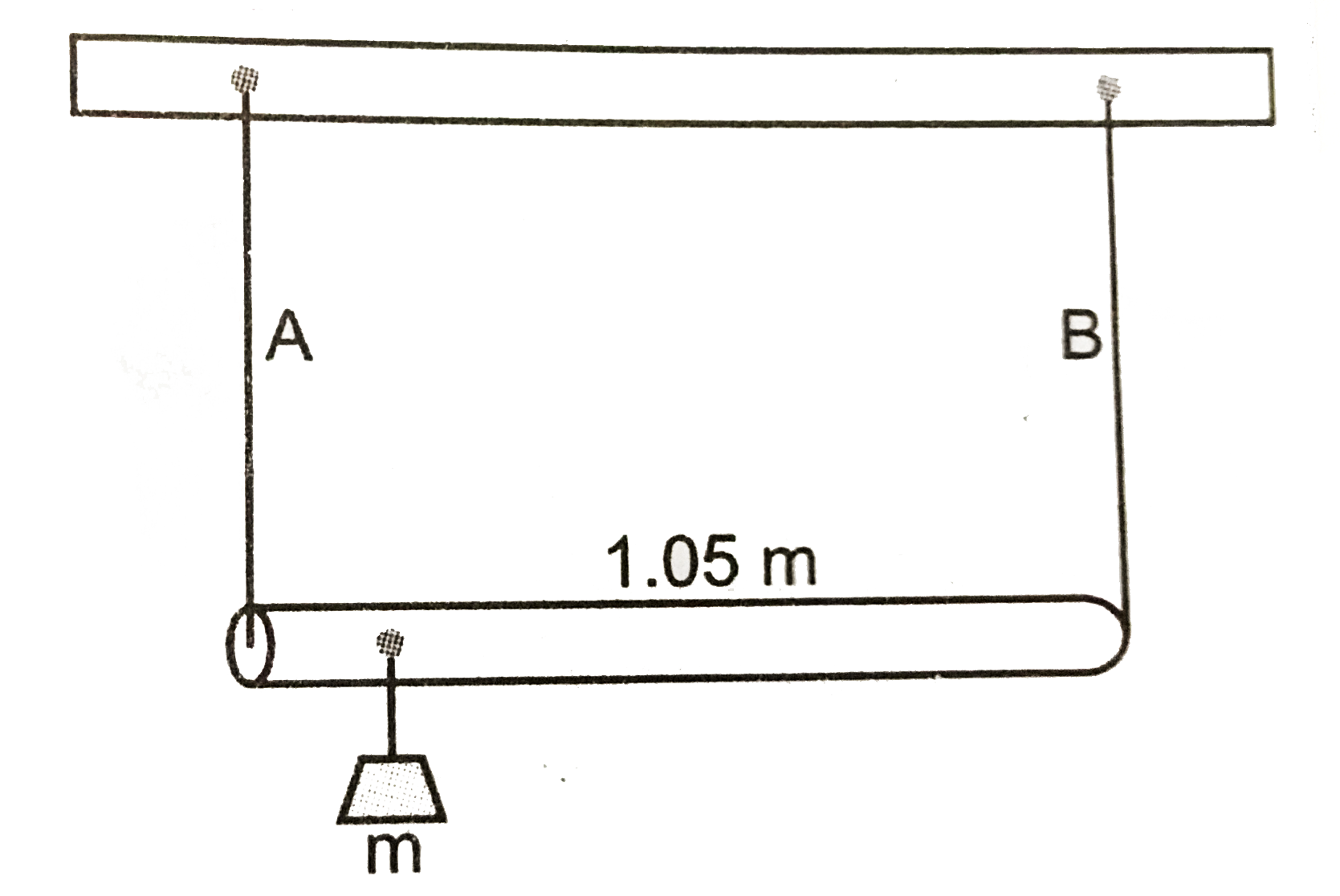
A rod of length 1 and negligible mass is suspended at its two ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in figure. The cross-sectional areas of wires A and B are 1.0mm2and2.0mm2 respectively. Ysteel”) = 200 xx 10 ^(9) Nm ^(-2) and Y_(auminium”=70×109Nm−2
 Solution in Gujrati
Solution in Gujrati
Mass m should be suspended close to wire A to have equal stresses in both the wires.
Mass m should be suspended close to B to have equal stresses in both the wires.
Mass m should be suspended at the middle of the wires to have equal stresses in both the wires.
Mass m should be suspended close to wire A to have equal strain in both wires.
The correct Answer is:B, D
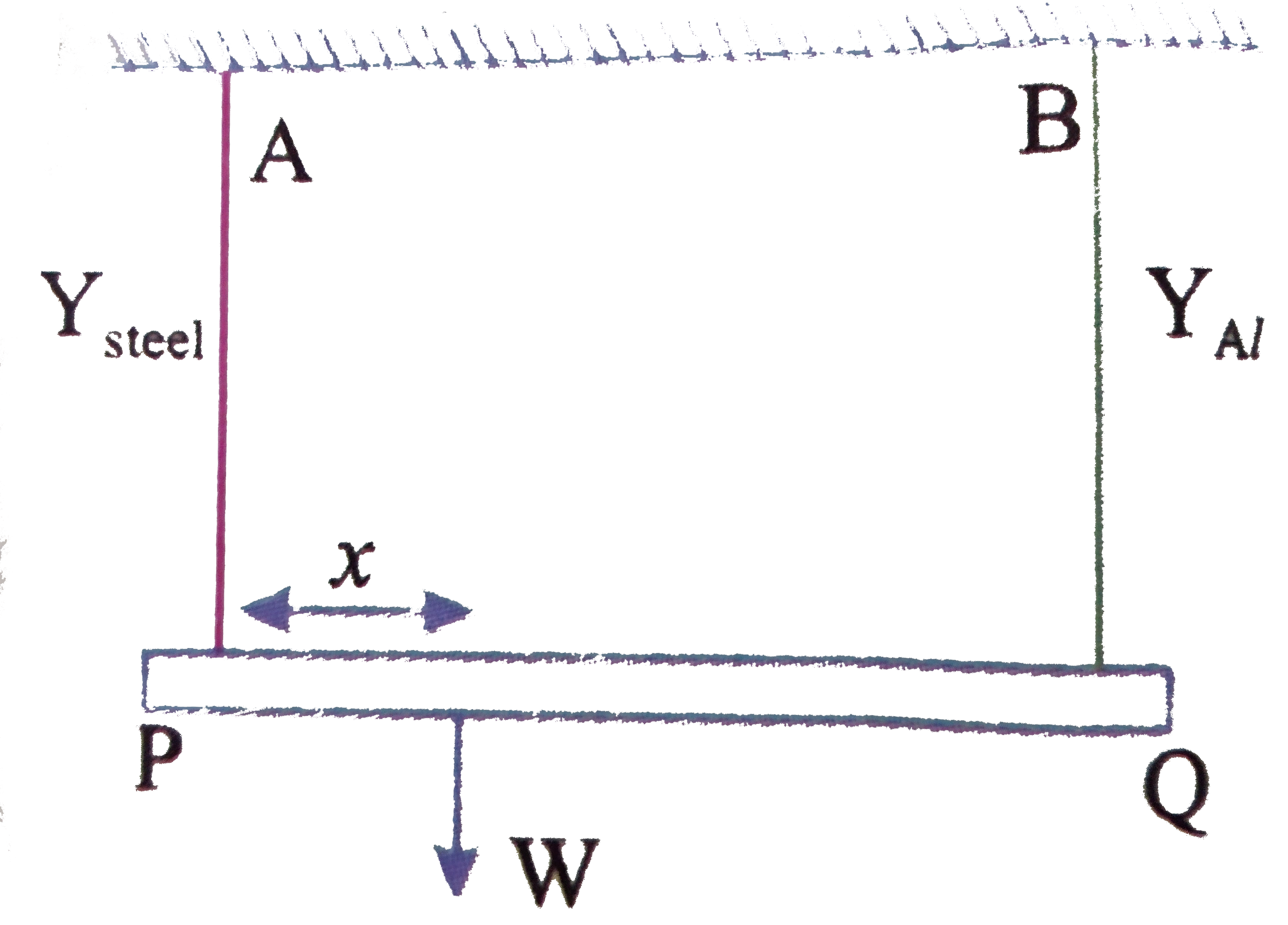
Suppose, mass m hangs at distance x from wire B.

Let 1 is for steel wire and 2 is for aluminium wire. T1andT2 are the tension in steel and aluminium wire respectively and S1andS2 are stress and ∈1and∈2are strain a1anda2 are cross sectional areas.
For balance of wire.
∑T=0
∴T2x−T1(l−x)=0
∴T2x=T(l−x)
∴T2T1=l−xx ...(1)
Stress:
For steel wire S1=T1a1 ...(2)
For aluminium wire S2=T2a2 ...(3)
If stress is equal,
S1=S2
∴T1a1=T2a2
∴T1T2=a1a2=1.02.0=12
∴xl−x=12[∵ From eq. (1)]
∴2x=l−x
∴3x=l
∴x=l3 is the distance from end B
and l−x=l−l3=2l3 is the distance from end A.
∴l3<2l3 hence option (B) is correct.
Now, if strain are same,
Y1=S1∈1.andY2=S2∈2
but ∈1=∈2
∴Y1Y2=S1S2
∴200×10970×109=T1a1×a2T2
[∵ From equation (2) and (3)]
∴207=T1T2×a2a1
∴207=xl−x×2.010[∵ From eq. (1)]
∴107=xl−x
∴10l−10x=7x
∴10l=17x
∴x=10l17 is the distance from end B
andl−x=l−10l17=7l17 is distance from end A.
∴7l17<10l17 hence option (D) is correct.
Topper's Solved these Questions
- MACHANICAL PROPERTIES OF SOLIDS BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-E
28 Videos
- MACHANICAL PROPERTIES OF SOLIDS BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-F
11 Videos
- MACHANICAL PROPERTIES OF SOLIDS BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-C
66 Videos
- LAW OF MOTIONBOOK - KUMAR PRAKASHANCHAPTER - LAW OF MOTIONEXERCISE - (QUESTION PAPER) SECTION-D
1 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - KUMAR PRAKASHANCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - QUESTION PAPER (SECTION -C)
3 Videos
Similar Questions
Two wires A and B are of the same material their lengths are in the ratio 1 : 2 and the diameter are in the ratio 2 : 1. If they are pulled by the same force, their increase in length will be in the ratio ........
View SolutionTwo wires are made of the same material and have the same volume. The first wire has cross sectional area A and the second wire has cross sectional area 3A. If the length of the first wire is increased by Δl on applying a force F, how much force needed to stretch the second wire by the same amount ?
View SolutionWhat is elasticity ? What is plastic body and plasticity?
View SolutionA 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
View SolutionGlycerine flows steadily through a horizontal tube of length 1.5m and radius 1.0 cm . If the amount of glycerine collected per second at one is 4.0×10−3kgs−1 , what is the pressure difference between the two ends of the tube ? (Density of glycerine =1.3×10103kgm−3 and viscosity of glycerine =0.83 Pa s). [ you may also like to check if the assumption of laminar flow in the tube is correct]
View SolutionA rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2
View SolutionA rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2

View SolutionA rod PQ of length 1.05m having negligible mass is supported at its ends by two wires one of stell (wire A), and the other of aluminium (wire B) of equal lengths as shown in fig. The cross-sectional areas of wires A and B are 1.0mm2 and 2.0mm2 respectively. At what point along the rod a load W be suspended in order to produce
(a) equal stress, (b) equal strains in both steel an aluminium.
(Ysteel=200GPa,Yaluminium=70GPa)
View SolutionA light rod of length 2 m is suspended ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is ade of steel and is of cross-section 0.1 cm and the other of brass of cross-section 0.2 cm. Along the rod at what distance a weight may be hung to produce stresses in the wires? (Y_("Steel") = 2 xx 10^(11) Nm^(-2), Y_("Bass") = 1 xx 10^(11) Nm^(-2))
View SolutionThe Young's modulus of brass and steel are respectively 1.0×1011Nm−2 and 2.0×1011Nm−2. A brass wire and a steel wire of the same length are extended by 1 mm each under the same force. If radii of bras and steel wires are RB and Rs respectively, then
View SolutionAn aluminium wire and a steel wire of the same length and cross-section are joined end- to-end. The composite wire is hung from a rigid support and a load is suspen-ded from the free end. If the increase in lengthe of the composite wire is 1.35 mm, find the ratio the (i) stress in the two wires amd (ii) strain in the two wires.
(YAl=0.7×10!1Nm−2,Ysteel=2=1011Nm−2)
View SolutionA rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1 mm^(2) and 2 mm^(2) , respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given, Y_(steel) = 2 xx 10^(11) Nm^(-2) and Y-(alumi n i um) = 7.0 xx 10^(10)N^(-2)
View Solutionl लम्बाई तथा उपेक्षणीय द्रव्यमान की कोई छड़ अपने दो सिरों पर समान लम्बाई की दो तारों से लटकाई गई है जिनमें एक तार स्टील (तार A) का तथा दूसरा एल्यूमीनियम (तार B) का है। तार A तथा B की अनुप्रस्थ-काट के क्षेत्रफल क्रमश: 1.0 मी 2 तथा 2.0 मिमी 2 हैं
(YAI=70×109 न्यूटन/मी 2 और Ysteel=200×109 न्यूटन/मी 2)
View SolutionA rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in figure. The cross-sectional areas of wires A and B are 1.0 mm^(2) and 2.0 mm^(2), respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
View SolutionA mass of 15 kg is tied at the end of a steel wire of the length lm. It is whirled in a vertical plane with angular velocity 1 rad/s. Cross sectional area of the wire is 0.06 cm^(2). Calculate the elongation of the wire when the mass is at its lowest position. Y_("steel”) = 2 xx 10 ^(11) Nm ^(-2)
View Solution
