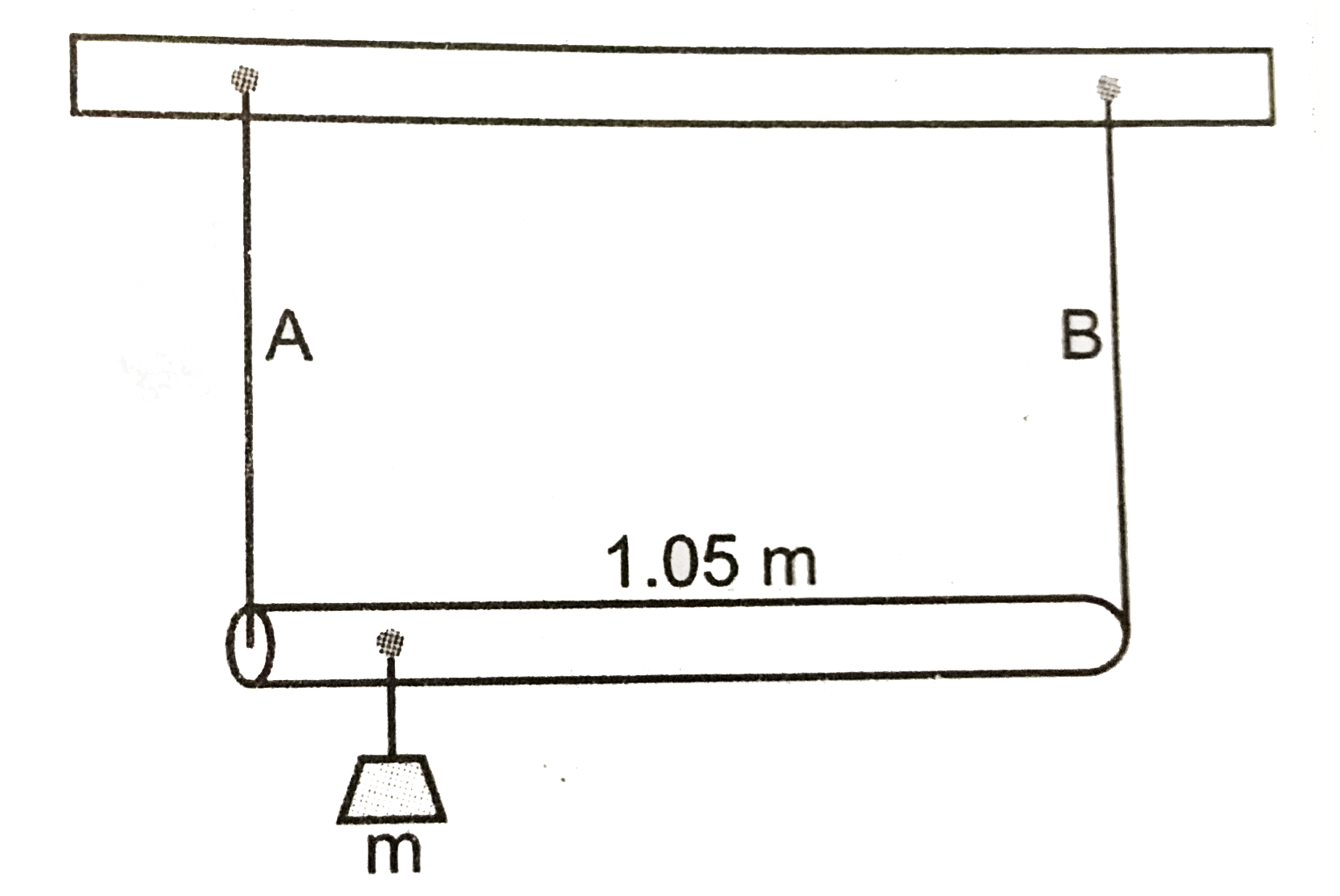
A rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2
Answer: (a) 0.7 m from the steel-wire end
(b) 0.432 m from the steel-wire end
Cross-sectional area of wire A, a1=1.0mm2=1.0×10−6m2
Cross-sectional area of wire B,a2=2.0mm2=2.0×10−6m2
Young’s modulus for steel, Y1=2×1011Nm−2
Young’s modulus for aluminium, Y2=7.0×1010Nm−2
(a) Let a small mass m be suspended to the rod at a distance y from the end where wire A is attached.
Stress in the wire= ForceArea=Fa
If the two wires have equal stresses, then:
F1a1=F2a2
Where,
F1 = Force exerted on the steel wire
F2 = Force exerted on the aluminum wire
F1F2=a1a2=12 ...(i)
The situation is shown in the following figure.

Taking torque about the point of suspension, we have:
F1y=F2(1.05−y)
F1F2=(1.05−y)y ...(ii)
Using equations (i) and (ii), we can write:
(1.05−y)y=12
2(1.05−y)=y
2.1−2y=y
3y=2.1
∴y=0.7m
In order to produce an equal stress in the two wires, the mass should be suspended at a distance of 0.7 m from the end where wire A is attached.
(b) Young's modulus = StressStrain
Strain = StressYoung's modulus=FaY
If the strain in the two wires is equal, then:
F1a1Y1=F2a2Y2
F1F2=a1a2Y1Y2=12×2×10117×1010=107 ...(iii)
Taking torque about the point where mass m, is suspended at a distance y1 from the side where wire A attached, we get:
F1F2=(1.05−y1)y1 ...(iii)
Using equations (iii) and (iv), we get:
(1.05−y1)y1=107
7(1.05−y1)=10y1
17y1=7.35
∴y1=0.432 m
In order to produce an equal strain in the two wires, the mass should be suspended at a distance of 0.432 m from the end where wire A is attached.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE
21 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE
31 Videos
- MOTION IN A PLANE BOOK - NCERT ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - EXERCISE
32 Videos
Similar Questions
A point mass m is suspended usin two wires of different material as shown in the figure. If corss-section of wire-1 and sore-2 are 3mm2and√3mm2 respectively, which of the following is correct?

View SolutionTwo wires of equal length and cross-section area suspended as shown in figure. Their Young's modulus are Y1 and Y2 respectively. The equavalent Young's modulus will be

View Solution
Knowledge Check
A light rod of length 2 m is suspended from ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 0.1 cm sq. and the other of brass of cross-section 0.2 cm sq. Along the rod at what distance a weight may be hung to produce equal stresses in the wires?
(YSteel=2×1011Nm−2,YBass=1×1011Nm−2)A43m from steel wireB43m from brass wireC1 m from steel wireD14m from brass wire
An iron rod B of length 1 m and mass 1 kg is suspended with help of two wires as shwon in figure. The area of cross-section of iron wire is 0.3 cm2 and of copper wire is 0.6cm2.
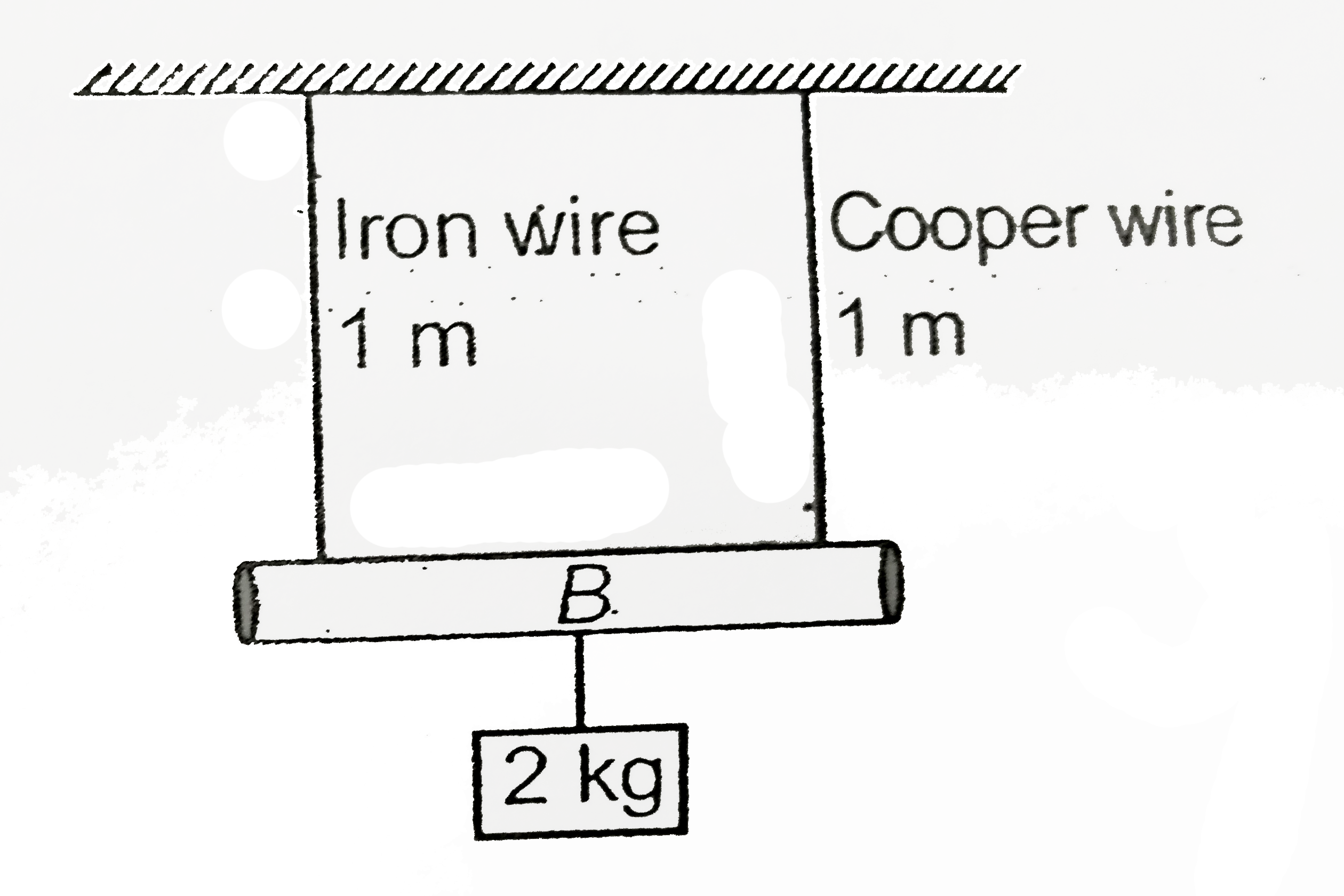
At what distance from iron wire a weight can be hung to produce equal stress in wires?
View SolutionA light rod AC of length 2.00 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 10−3m2 and the other is of brass of cross-section 2×10−3m2. The position of point D from end A along the rod at which a weight may be hung to produce equal stress in both the wires is [Young's modulus of steel is 2×1011Nm2 and for brass is 1×1011Nm−2]

View SolutionTwo wires of the same material and same length have radii 1 mm and 2 mm respectively. Compare :
their resistances,
View SolutionA steel wire and a copper wire of equal length and equal cross- sectional area are joined end to end and the combination is subjected to a tension. Find the ratio of
copper/steel
(a) the stresses developed . In the two wires,
(b) the strains developed. (Y of steel =2×1011N/m2)
View SolutionFour wires of equal length 2 m are arranged as shown in the figure. Wires , 2, 3 and 4 are of equal cross-sectional area and wire 1 is of half the cross section of these wires. By how much distance pointer at point 5 must be moved to get null point ?
View SolutionA wire of length 1m and radius 1mm is subjected to a load. The extension is x.The wire is melted and then drawn into a wire of square cross - section of side 2mm Its extension under the same load will be
View SolutionAn iron rod B of length 1 m and mass 1 kg is suspended with help of two wires as shwon in figure. The area of cross-section of iron wire is 0.3 cm2 and of copper wire is 0.6cm2.

In the above question, if Yiron:YCu=2:1, then the ratio of elastics energy per unit volume stored in iron wire to copper wire is
View Solution
