A rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v.F∈dtheemf∈duced∈thewirewhenitsdistance∈thewirewhenitsdistanceomthelongwireisx.
To find the induced electromotive force (emf) in a rod of length l that is moving away from a long wire carrying a constant current i, we can follow these steps:
Step 1: Understand the Setup
We have a long straight wire carrying a constant current i. A rod of length l is moving away from this wire with a velocity v. At a given moment, the distance of the rod from the wire is x.
Step 2: Determine the Magnetic Field
The magnetic field B around a long straight wire carrying current i at a distance x is given by the formula:
B=μ0I2πx
where μ0 is the permeability of free space.
Step 3: Identify the Directions
- The direction of the magnetic field B due to the current in the wire can be determined using the right-hand thumb rule. For a current flowing in the positive direction, the magnetic field circles around the wire in a counter-clockwise direction. At the position of the rod, the magnetic field will be directed into the plane of the paper (negative k direction).
- The velocity v of the rod is in the positive x direction.
- The length l of the rod is oriented in the positive y direction.
Step 4: Use the Formula for Induced EMF
The induced emf (E) in the rod can be calculated using the formula:
E=L⋅(V×B)
where:
- L is the length vector of the rod (in the j direction),
- V is the velocity vector of the rod (in the i direction),
- B is the magnetic field vector (in the negative k direction).
Step 5: Calculate the Cross Product
Substituting the vectors:
- L=l^j
- V=v^i
- B=−μ0I2πx^k
We calculate V×B:
V×B=(v^i)×(−μ0I2πx^k)=−μ0Iv2πx(^i×^k)=−μ0Iv2πx(−^j)=μ0Iv2πx^j
Step 6: Calculate the Induced EMF
Now substituting back into the emf formula:
E=l^j⋅(μ0Iv2πx^j)=l⋅μ0Iv2πx=μ0Ivl2πx
Final Result
Thus, the induced emf in the rod when its distance from the wire is x is:
E=μ0Ivl2πx
---
We have a long straight wire carrying a constant current i. A rod of length l is moving away from this wire with a velocity v. At a given moment, the distance of the rod from the wire is x.
The magnetic field B around a long straight wire carrying current i at a distance x is given by the formula:
B=μ0I2πx
where μ0 is the permeability of free space.
- The direction of the magnetic field B due to the current in the wire can be determined using the right-hand thumb rule. For a current flowing in the positive direction, the magnetic field circles around the wire in a counter-clockwise direction. At the position of the rod, the magnetic field will be directed into the plane of the paper (negative k direction).
- The velocity v of the rod is in the positive x direction.
- The length l of the rod is oriented in the positive y direction.
The induced emf (E) in the rod can be calculated using the formula:
E=L⋅(V×B)
where:
- L is the length vector of the rod (in the j direction),
- V is the velocity vector of the rod (in the i direction),
- B is the magnetic field vector (in the negative k direction).
Substituting the vectors:
- L=l^j
- V=v^i
- B=−μ0I2πx^k
V×B=(v^i)×(−μ0I2πx^k)=−μ0Iv2πx(^i×^k)=−μ0Iv2πx(−^j)=μ0Iv2πx^j
Now substituting back into the emf formula:
E=l^j⋅(μ0Iv2πx^j)=l⋅μ0Iv2πx=μ0Ivl2πx
Thus, the induced emf in the rod when its distance from the wire is x is:
E=μ0Ivl2πx
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Single Correct
79 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.1
15 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance ‘a’ from the wire.
View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View Solution
Knowledge Check
Figure shows an irregular shapped wire AB moving with velocity v. Find the emf induced in the wire :-
AVBlsinθBV2BlsinθCVBlcosθDVBlElectric charge q is distributed uniformly over a rod of length l. The rod is placed parallel to a ling wire carrying a current i. The separation between the rod and the wire is . The force needed to move the rod along its length with a uniform velocity v is
Aμ0iqv2πaBμ0iqv4πaCμ0iqvl2πaDμ0iqvl4πaFor a long wire of charge density γ,, field at a distance r from the wire is
Aγ2πε0rnBγ4πε0rnC0Dkqεe
Shows an irregular shaped wire AB moving with velocity v. Find the emf induced in the wire.

View SolutionA rectangular loop is moving parallel to a long wire carrying current i with a velocity v. Find the emf induced in the loop (Fig. 3.68) if its nearest end is at a distance a from the wire. Draw equivalent electrical diagram.

View SolutionElectric charge q is uniformly distributed over a rod of length / The rod is placed parallel to a long wire carrying a current I The separation between the rod and the wire is a find the force needed to move the rod along its length with a uniform velocity v
View SolutionA conducting rod MN moves with a speed v parallel to a long straight wire which carries a constant current i, as shown in fig. The length of the rod is normal to the wire. Find the emf induced in the total length of the rod. State which end will be at a lower potential.
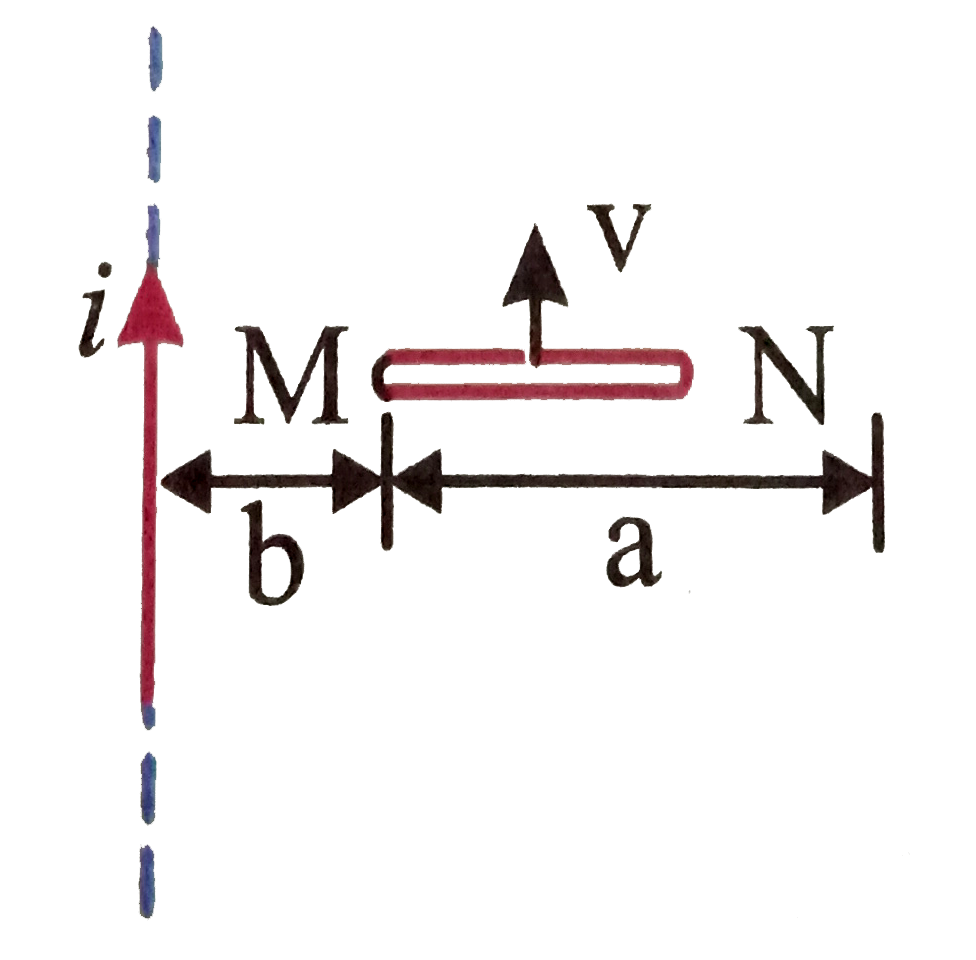
View SolutionA square metallic loop of side l is placed near a fixed long wire carrying a current i(figure).The loop is moved towards right perpendicular to the wire with a speed v in the plane containing the wire and the loop.The emf induced in the loop when the rear end of the loop is at a distance a=2l from the wire is μ0ivxπ.Find out value of x.

View Solution
