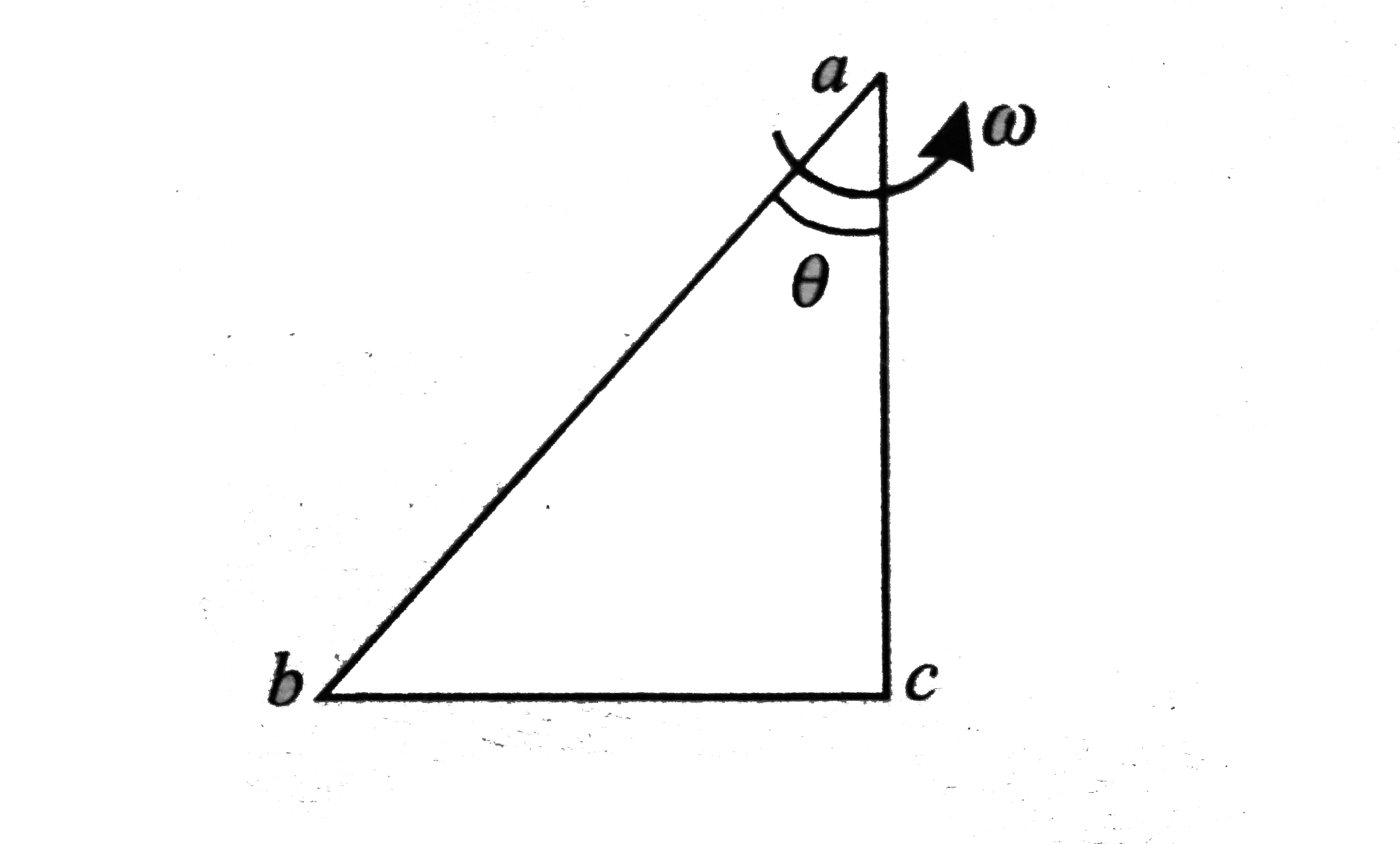
A rod of length L rotates in the form of a conical pendulum with an Angular velocity ω about its axis as shown in Fig. 3.165. The rod makes an angle θ with the axis. The magnitude of the motional emf developed across the two emf of the rod is

(a) 12BωL2
(b) 12BωL2tan2θ
( c) 12BωL2cos2θ
(d) 12BωL2sin2θ
The correct Answer is:D
(d) ε=∫(→v×→B).→dl

→ε=∫[(lsinθ)ωˆk)×B(−ˆj)].[dlsinθ(−ˆi)+dlcosθ(−gat(j))]
→ε=∫[Bωsinθ−ˆi].[dlsinθ(−ˆi)+dlcosθ(−ˆj)]
=−Bωsin2θ∫L0ldl=−12Bωsin2θL2
→ε=Vb−Va=−12BωL2sin2θ
Negative sign indicates that end b will be negative w.r.t.a.
Alternate Method:
Consider two more conductors ac and bc. This comletes a closed loop. The net emf inducd in this closed loop should be zero, as net flux through this loop always remains zero.
eab+ebc+eca=0
but ebc=12Bω(Lsinθ)2,eca=0 putting the values, we get
eab=−12Bω(Lsinθ)2
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A rod is rotating with angular velocity ω about axis AB. Find cosθ.

View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical

View Solution
Knowledge Check
A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
ABl2ω2BzeroC(Bl2ω8)D2Bl2ω
A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What will be the horizontal component of angular momentum of the rod about the point of suspension in terms of m, ω, l and θ.

View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA metallic rod of length I rotates at angular velocity ω about an axis passing through one end and perpendicular to the rod. If mass of electron is m and its charge is -e then the magnitude of potential difference between its two ends is
View Solution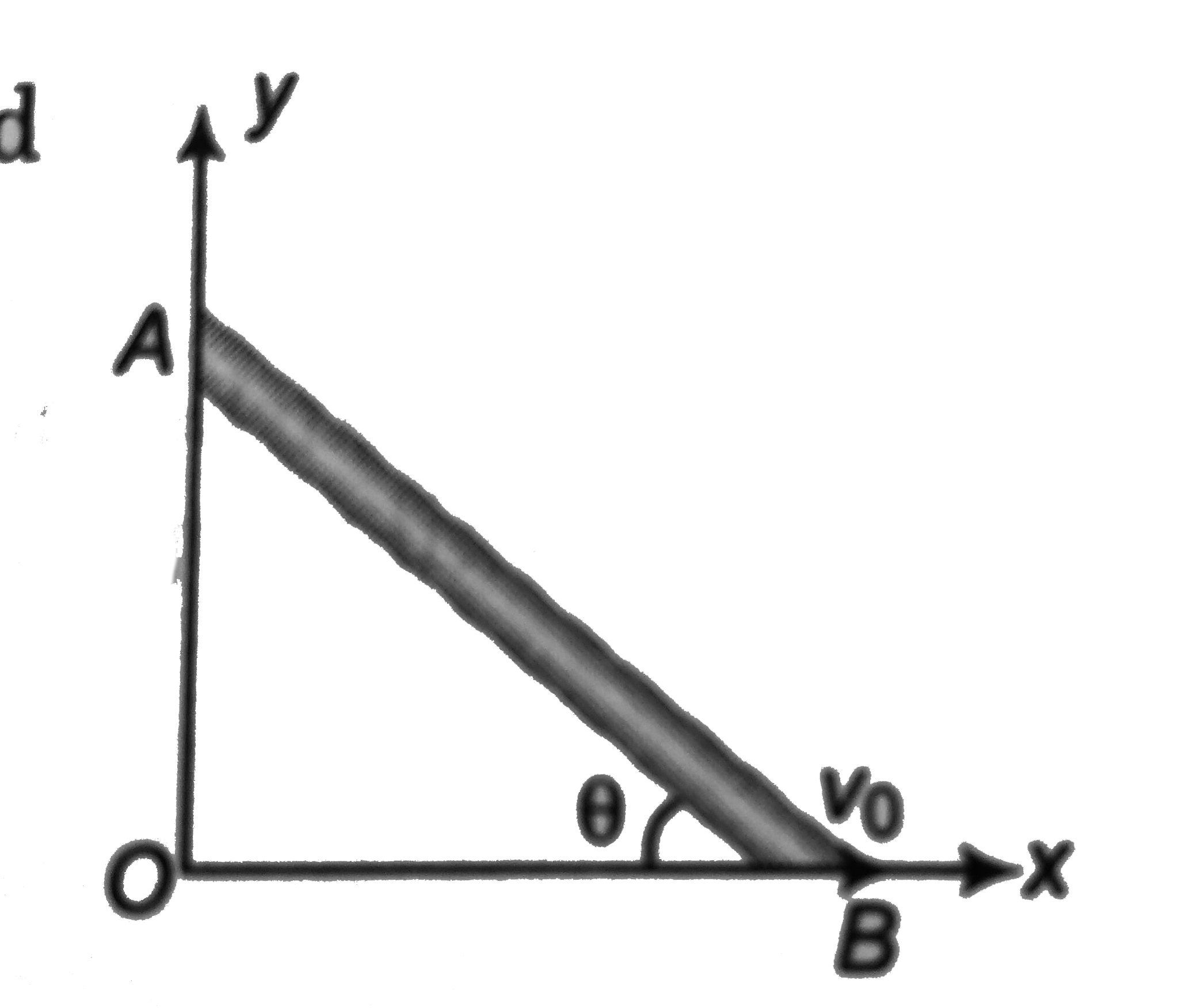
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity vv as shown. The length of the rod is l.
View SolutionA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View Solution
