A rod of mass $m$ and length $l$ is rotating about a fixed point in the ceiling with an angular velocity $ω$ as shown in the figure. The rod maintains a constant angle $θ$ with the vertical.
What is the rate of change of angular momentum of the rod ?

$\frac{m ω^{2} l^{2} sin θ}{6}$

$\frac{m ω^{2} l^{2} sin 2 θ}{6}$

$\frac{m ω^{2} l^{2} {sin}^{2} θ}{6}$

$\frac{m ω^{2} l^{2} {cos}^{2} θ}{6}$

Video Solution

Text Solution

Verified by Experts

The vertical component of the angular momentum remains constant while its horizontal component keeps changing the direction.
$d L = \frac{m ω l sin (2 θ)}{6} \times ω d t \Rightarrow \frac{d L}{d t} = \frac{m ω^{2} l^{2}}{6} sin (20)$

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

A rod of mass $m$ and length $l$ is rotating about a fixed point in the ceiling with an angular velocity $ω$ as shown in the figure. The rod maintains a constant angle $θ$ with the vertical.
What will be the horizontal component of angular momentum of the rod about the point of suspension in terms of $m$ , $ω$ , $l$ and $θ$ .

View Solution
A rod of mass $m$ and length $l$ is rotating about a fixed point in the ceiling with an angular velocity $ω$ as shown in the figure. The rod maintains a constant angle $θ$ with the vertical.
What angle will the rod make with the vertical

View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end $O$ with an angular velocity $ω = 4 r a d / s$ . Find angular momentum of the rod about the axis rotation.
View Solution
A rod is rotating with angular velocity $ω$ about axis AB. Find $cos θ$ .

View Solution
A rod of length $L$ rotates in the form of a conical pendulum with an Angular velocity $ω$ about its axis as shown in Fig. 3.165. The rod makes an angle $θ$ with the axis. The magnitude of the motional emf developed across the two emf of the rod is

View Solution
A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle $θ$ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed $V$ in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle $θ$ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed $V$ in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution
A uniform rod of mass $m$ and length $l$ is pivoted smoothly at $O$ . A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation $θ .$
b.What is the maximum angular displacement of the rod?

View Solution
A rod of mass $m$ and length $l$ is connected with a light rod of length $l$ . The composite rod is made to rotate with angular velocity $ω$ as shown in the figure. Find the

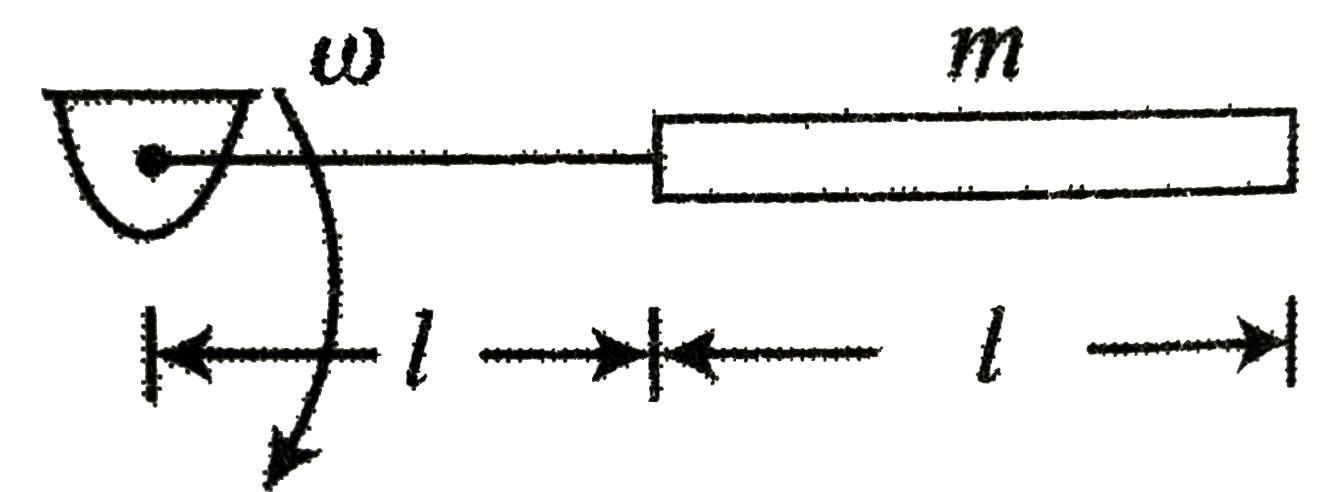
a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.
View Solution

A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical. What is the rate of change of angular momentum of the rod ?

The vertical component of the angular momentum remains constant while its horizontal component keeps changing the direction. dL=mωlsin(2θ)6×ωdt⇒dLdt=mω2l26sin(20)

Similar Questions

Recommended Questions

A rod of mass $m$ and length $l$ is rotating about a fixed point in the ceiling with an angular velocity $ω$ as shown in the figure. The rod maintains a constant angle $θ$ with the vertical.
What is the rate of change of angular momentum of the rod ?

The vertical component of the angular momentum remains constant while its horizontal component keeps changing the direction.
$d L = \frac{m ω l sin (2 θ)}{6} \times ω d t \Rightarrow \frac{d L}{d t} = \frac{m ω^{2} l^{2}}{6} sin (20)$