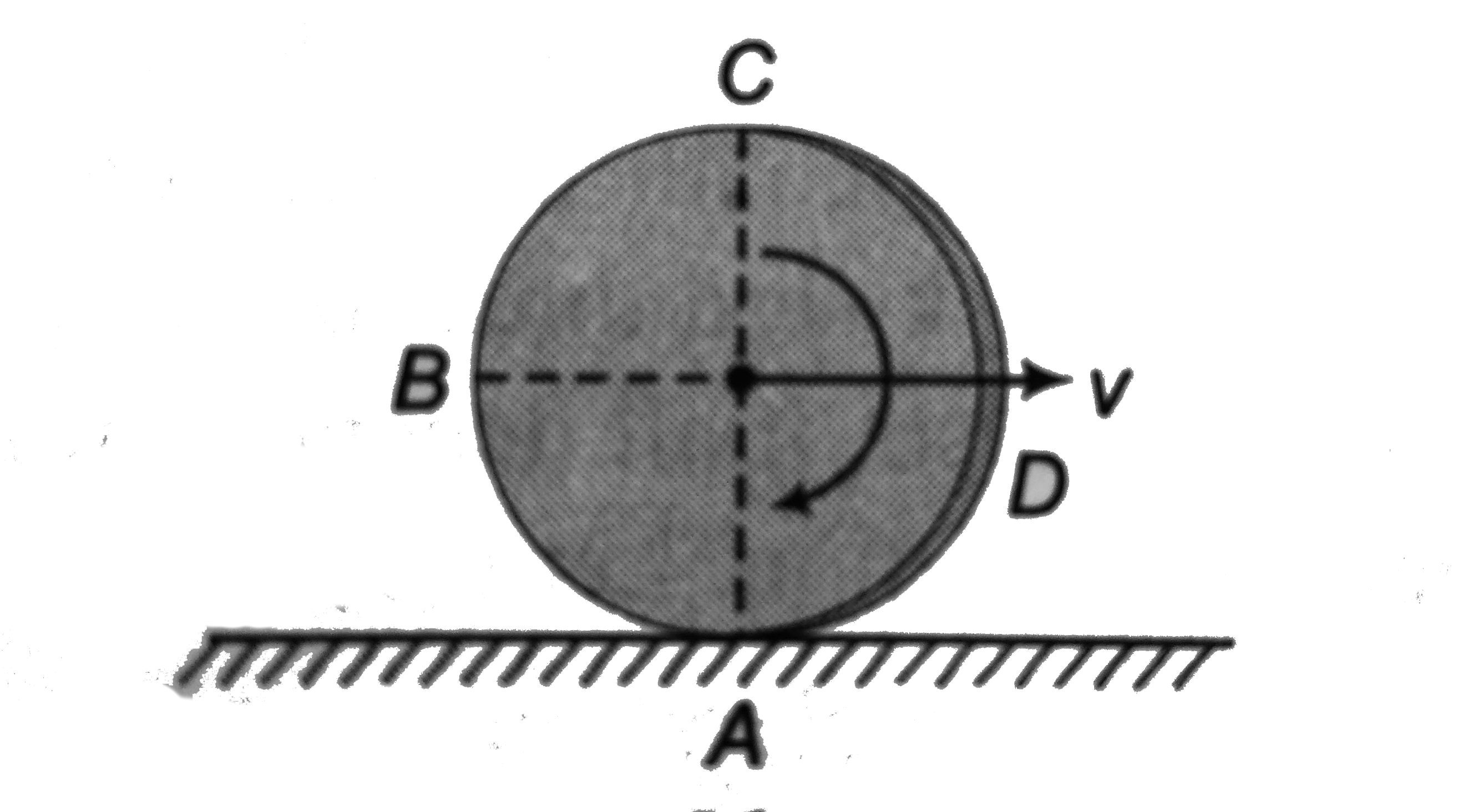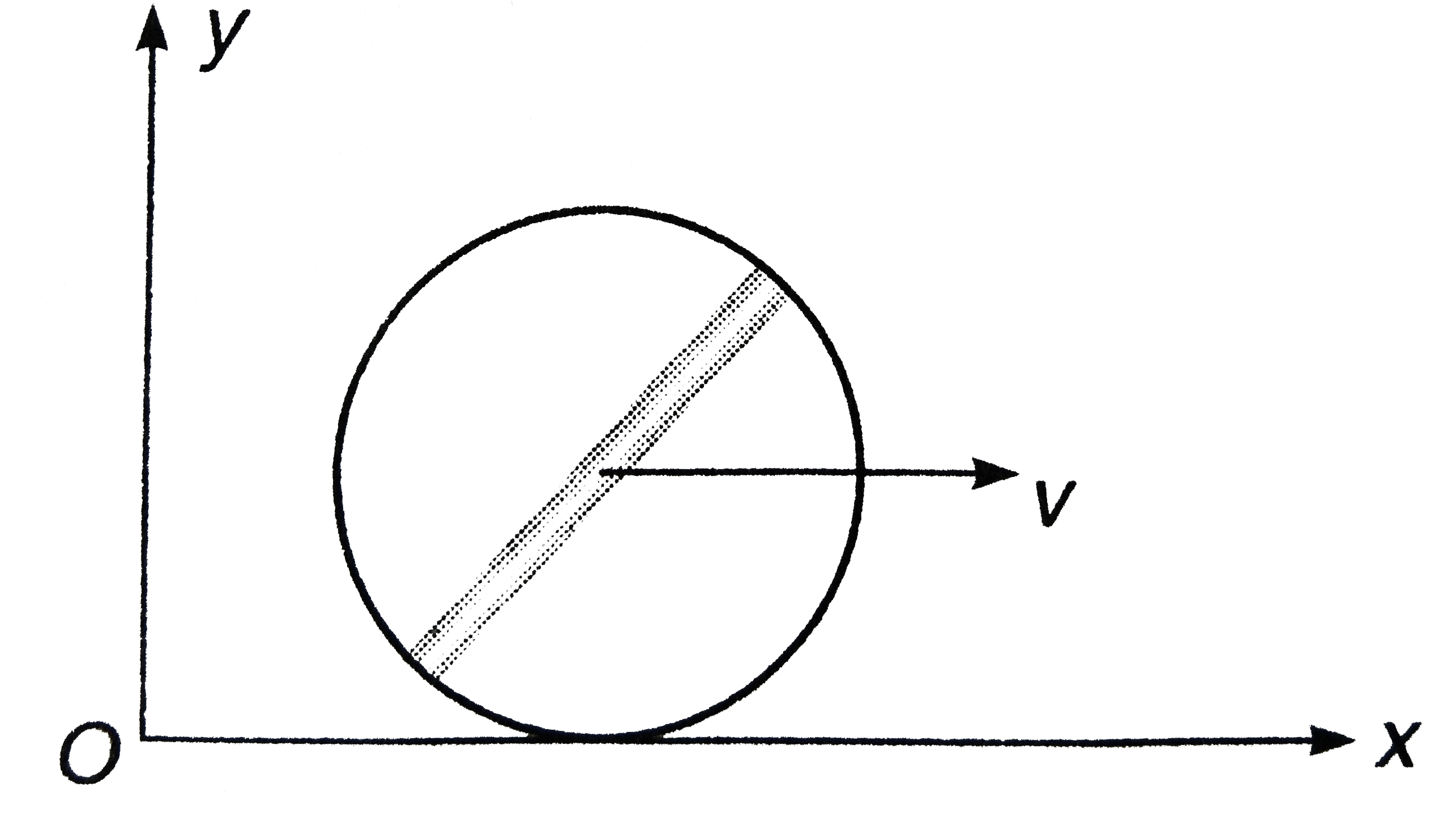
A rod of mass m and length 2 R is fixed along te diameter of a ring of same mass m and radius R as shown in figure. The combined body is rolling without slipping along x-axis find the angular momentum about z-axis.
Centre of mass of both lies at the centre of ring
IC=mR2+m(2R)212
=43mR2
L=(2mvr⊥)+ICω
=(2mvR)+43mR2(vR)
=103mvR
This is clockwise, or along negative z-axis.
∴L=(−103mvR)ˆk
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective
30 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Knowledge Check
A ring of mass M and radius R is at rest at the top of an incline as shown. The ring rolls down the plane without slipping. When the ring reaches bottom, its angular momentum about its centre of mass is:
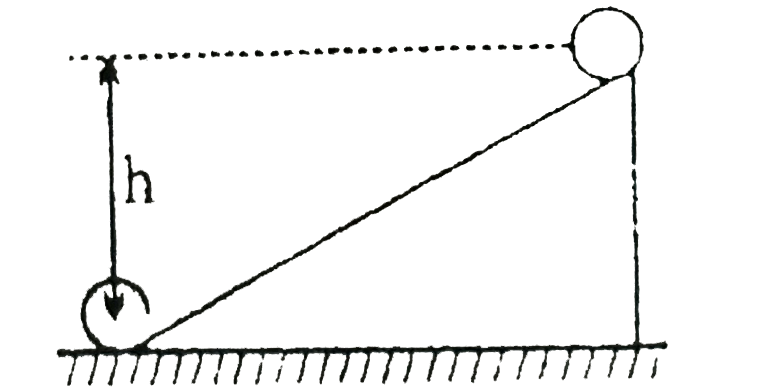 AMR√ghBMR√gh2CMR√2ghDnone
AMR√ghBMR√gh2CMR√2ghDnoneThe M.I. of a thin ring of mass M and radius R about an axis through the diameter in its plane will be:
A12MR2B32MR2CMR2D2MR2The M.I. of a ring of mass M and radius R about a tangential axis perpendicular to its plane is :
A2MR2BMR2C3/2MR2D3/4MR2
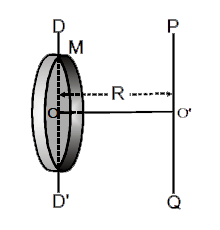
The moment of inertia of a ring of mass M and radius R about PQ axis will be :-
View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.


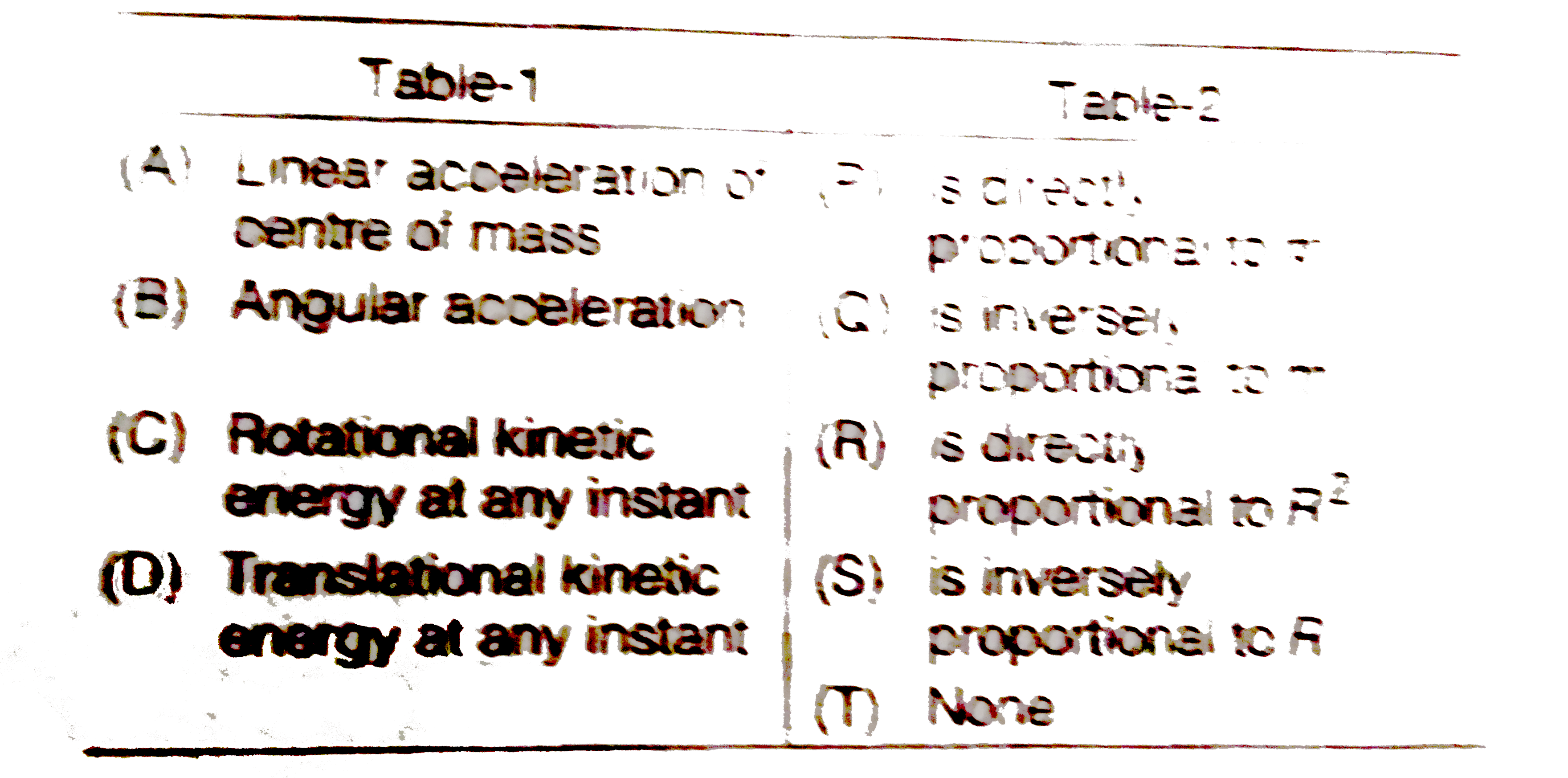
View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View SolutionA point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.
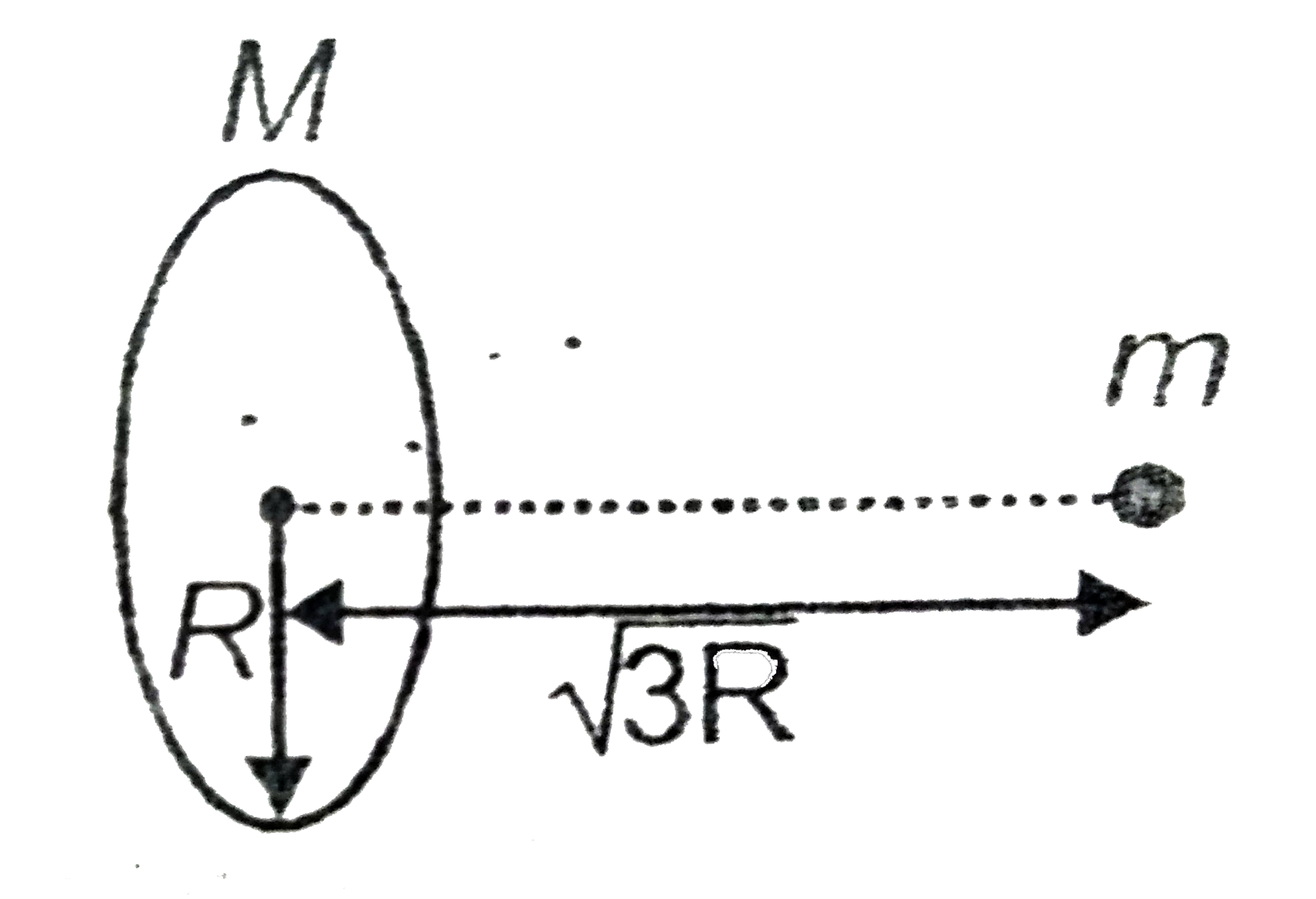
View SolutionA disc of mass m and radius R is attached to a rectangular plate of the same mass m, breadth R and length 2R as shown in figure. The moment of inertia of the system about the axis AB passing through the centre of the disc and along the plane is I=1α(313mR2).
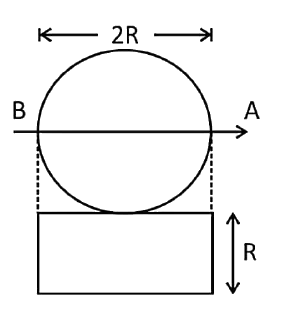
View Solution