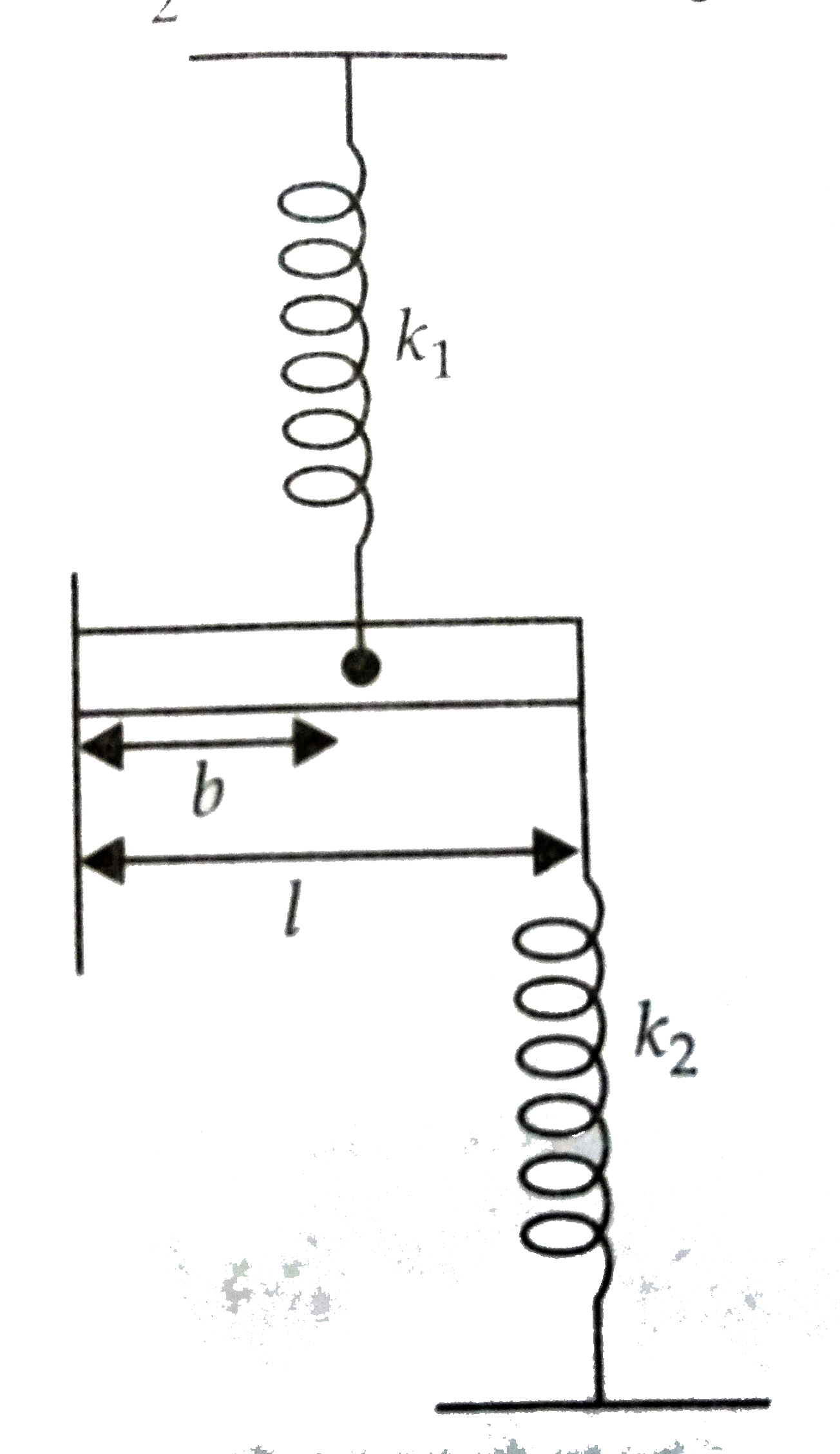
A rod of mass m and length l is connected by two spring of spring constants k1andk2, so that it is horizontal at equilibrium. What is the natural frequency of the system?
12π√k1b2+k2l2ml2
12π√2k1b2+k2l2ml2
12π√k1b2+k2l22ml2
12π√3(k2b2+k2l2)ml2
The correct Answer is:D
Let rod is displaced by an angle θ, taking torque about edge of rod
kbbθ×bcosθ+k2<hη×lcosθ=−Id2θdt2
Here, I=ml23andθ is small cosθ≈1
∴ml2α3+(k1b2+k2l2)θ=0
⇒α=−3(k1b2+k2l2)θml2
∴ω=√3(k1b2+k2l2)ml2
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTIPSCHAPTER - OSCILLATIONS EXERCISE - NCERT Exemplar
10 Videos
- OSCILLATIONS BOOK - NCERT FINGERTIPSCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems
1 Videos
- OSCILLATIONS BOOK - NCERT FINGERTIPSCHAPTER - OSCILLATIONS EXERCISE - Forced Oscillation And Resonance
6 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion And Reason
15 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTIPSCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions

A rod of mass m and length l hinged at one end is connected by two springs of spring constant k1 and k2 so that it is horizontal at equilibrium What is the angular frequency of the system? (in rads) (Take l=1m,b=14m,K1=16Nm,K2=61Nm.
View SolutionTwo spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

View Solution
Knowledge Check
Two spring of spring constant k1 and k2 are joined in series The effective spring constant of the combination is given by
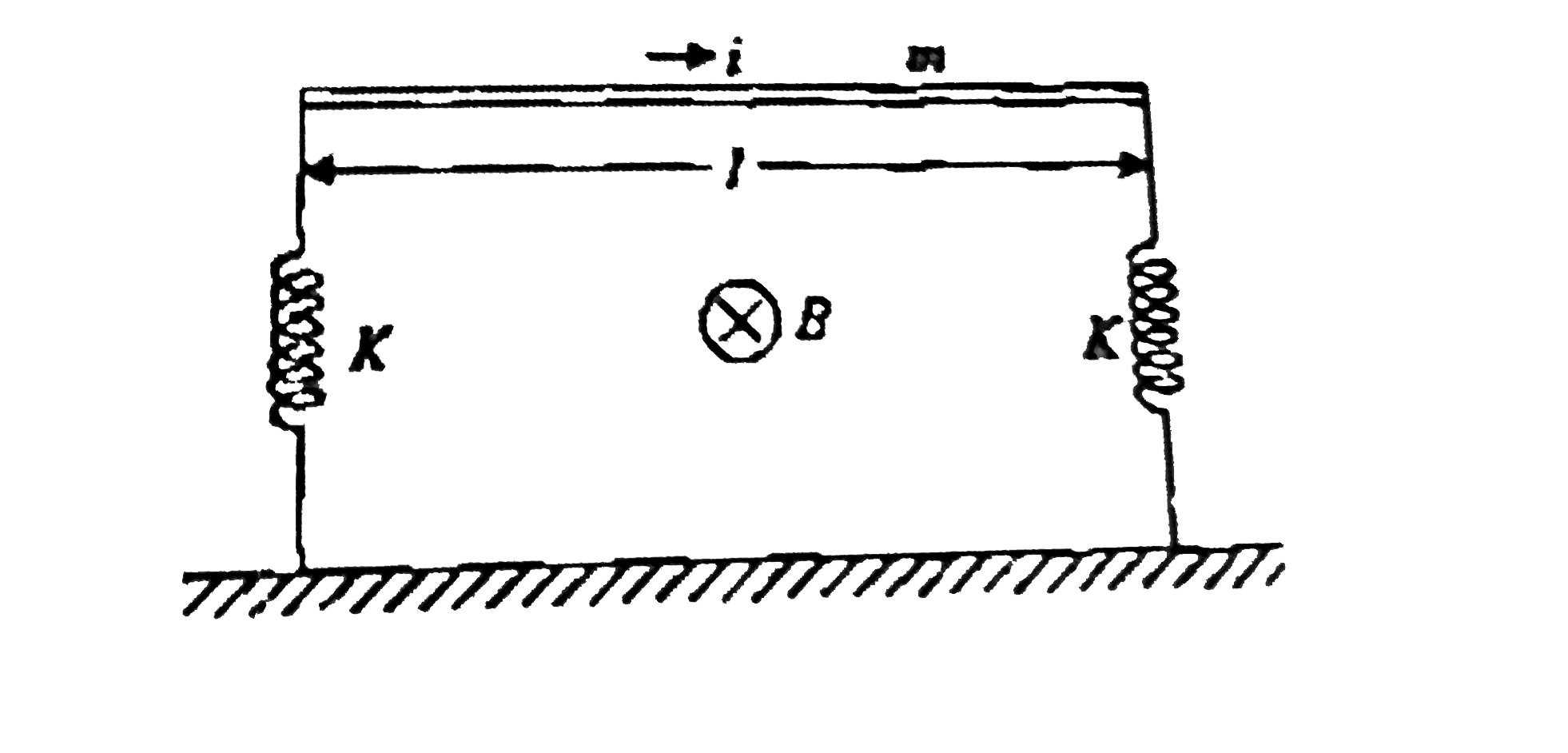
A√k1k2B(k1+k2)/2Ck1+k2Dk1k2k1+k2A horizontal metallic rod of mass 'm' and length 'l' is supported by two vertical identical springs of spring constant 'K' each and natural length l0. A current 'i is flowing the the rod in the direction shown. If the rod is in equilibrium, then the lengthof each spring in this state is:
 Alo+ilB−mgKBlo+ilB−mg2KClo+mg−ilB2KDlo+mg−ilBK
Alo+ilB−mgKBlo+ilB−mg2KClo+mg−ilB2KDlo+mg−ilBKA bob of mass m is connected to a spring of spring constant k and a string which is fixed to the ceiling as shown in figure. Original length of the spring is L and the bob rotates in a horizontal circle centred at the fixed rod. Assuming the spring remains horizontal, then elongation in the spring is :
 A(mg−mω2L)tanθmω2+kBmgtanθ+mω2Lmω2−kCmgtanθ+mω2LkDgtanθ−ω2Lω2−k/m
A(mg−mω2L)tanθmω2+kBmgtanθ+mω2Lmω2−kCmgtanθ+mω2LkDgtanθ−ω2Lω2−k/m
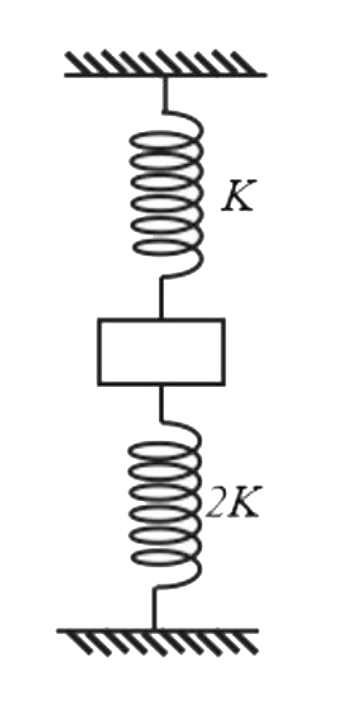
A block of mass m is connected between two springs (constants K1 and K2) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-

View SolutionA block of mass m is connected two springs of spring constant 2k annd k , respectively , as shown in the vertical plane. At equilibrium , both springs are compressed by same length. If suddenly lower spring is cut, then acceleration of block, just after spring cut , is
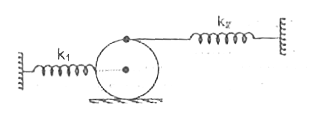
View SolutionA disk of mass m is connected to two springs of stiffness k1andk2 as shown in the figure. Find the angular frequency of the system for small oscillation. Disc can roll on the surface without slipping
View SolutionA horizontal metallic rod of mass m and length l is supported by two vertical identical springs of spring constant k each and natral length i0 A current l is flowing in the rod in the direction shown if the rod is in equilibrium then the length of each spring in this state is:
View SolutionTwo blocks of masses m, and m, are connected to the ends of a spring of spring constant k. System is kept at rest on a frictionless horizontal floor with spring in its natural length. Both the blocks are pulled along opposite directions with forces of same magnitude F. Calculate maximum elongation of spring and distances travelled by the blocks during this motion.
View Solution
