Two blocks of masses m, and m, are connected to the ends of a spring of spring constant k. System is kept at rest on a frictionless horizontal floor with spring in its natural length. Both the blocks are pulled along opposite directions with forces of same magnitude F. Calculate maximum elongation of spring and distances travelled by the blocks during this motion.

Text Solution

Verified by Experts

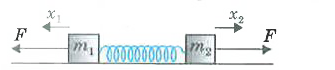
Net force in the horizontal direction is zero hence acceleration of centre of mass is zero. Initially, both the blocks are at rest hence initial velocity of centre of mass is zero. So we can conclude that centre of mass remains at rest and both the blocks come to momentary rest simultaneously at the time of maximum elongation.
Let $x_{1} and x_{2}$ be the distances travelled by the blocks during this period in opposite directions as shown in figure. We can understand that $(x_{1} + x_{2})$ will be maximum elongation of spring
Using conservation of energy we can write the following:
Work done by both the forces = Energy stored in spring
$F x_{1} + F x_{2} = \frac{1}{2} k {(x_{1} + x_{2})}^{2}$
$x_{1} + x_{2} = \frac{2 F}{K} ... . (1)$
Hence 2Fis maximum elongation of the spring, Here we know that displacement of centre of mass is zero so we can write the following equation:
$m_{1} x_{1} = m_{2} x_{2} ... . (2)$
Solving the above two equations we can find $x_{1} and x_{2}$
$x_{1} = \frac{m_{2}}{m_{1} + m_{2}} [\frac{2 F}{K} A n d x_{2} = \frac{m_{1}}{m_{1} + m_{2}} [\frac{2 F}{k}]$

Updated on:21/07/2023

Two blocks of masses $m_{1}$ and $m_{2}$ are connected by an ideal sprit, of force constant $k$ . The blocks are placed on smooth horizontal surface. A horizontal force $F$ acts on the block $m_{1}$ . Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring
Azero
B $\frac{F (m_{1} + m_{2})}{m_{1} m_{2}}$
C $\frac{F}{m_{1}}$
D $\frac{F}{m_{1} + m_{2}}$
Blocks A&B of mass m each are connected with spring of constant k both blocks lie on frictionless ground and are imparted horizontal velocity v as shown when spring is unstretched find the maximum stretch of spring.

A $v \sqrt{\frac{m}{k}}$
B $v \sqrt{\frac{m}{2} k}$
C $v \frac{\sqrt{2 m}}{k}$
Dnone
A block of mass $m$ connected to a spring of stiffness $k$ is placed on horizontal smooth surface. When block is at $x = 0$ , spring is in natural length. The block is also subjected to a force $F = \frac{k | x |}{\circ}$ then
AMotion of block is SHM
BTime period of motion is $π \sqrt{\frac{m}{k}} [\sqrt{2} + \sqrt{\frac{2}{3}}]$
CTime period of motion is $π \sqrt{\frac{m}{k}} [1 + \sqrt{\frac{3}{2}}]$
DSum of potential energy and kinetic energy of spring block system is maximum at right extreme.