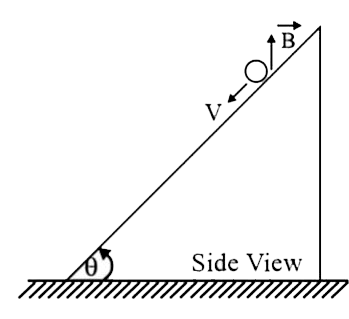
A rod of mass m, length l and resistance R is sliding down on a smooth inclined parallel rails with a cinstant velocity v. If a uniform horizontal magnetic field B exists, then find thevalue of B.
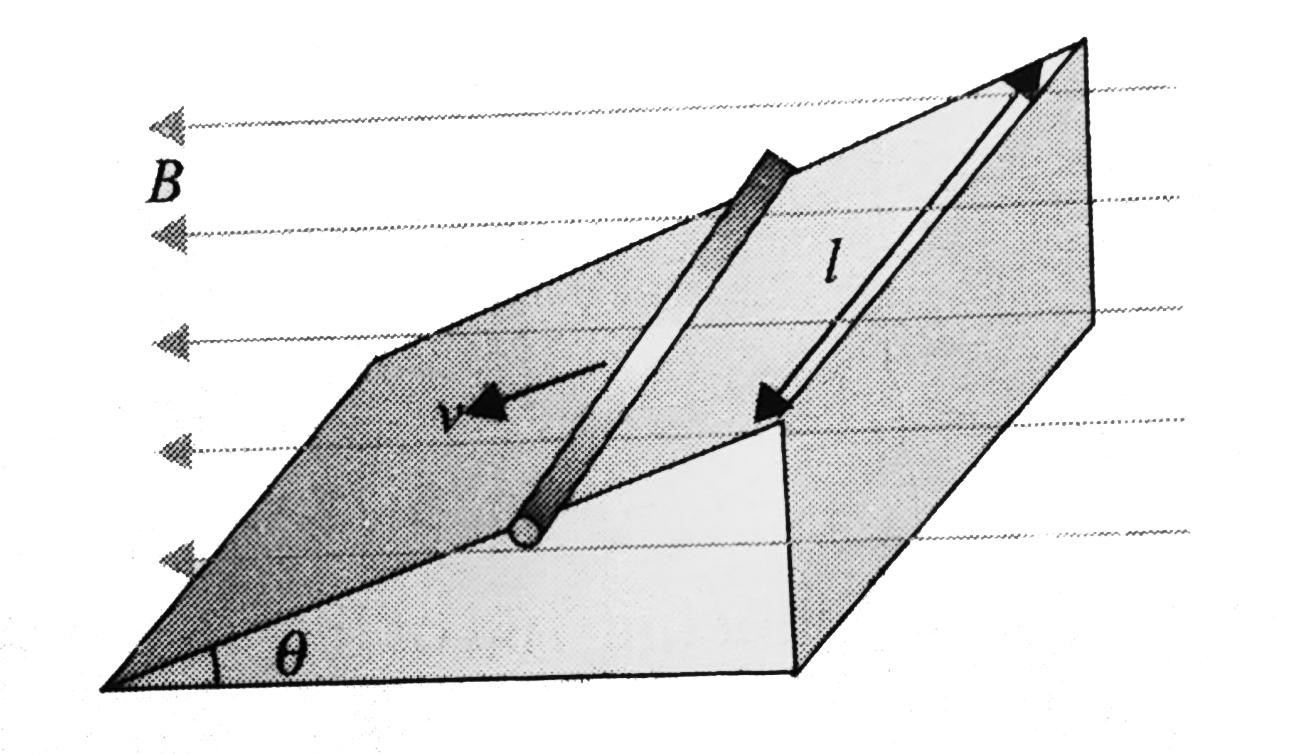

The emf induced in the rod,
E=(Bsinθ)lv
=Blvsinθ
The current in the circuit I=ER=BlvsinθR
Magnetic force acting on the sliding rod, Fmag=IlB
Fmag=(BlvsinθR)lB
=B2l2vsinθR
If the rod is sliding with constant velocity,
Fmagsinθ=mgsinθ
→ =B2l2vsin2θR=mgsinθ
→ B=√mgRl2vsinθ
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Single Correct
79 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.1
15 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A glass rod of length l moves with velocity in a uniform magnetic field B. What is the e.m.f. induced in the rod ?
View SolutionA straight horizontal conductor PQ of length l, and mass_ m slides down on two smooth conducting fixed parallel rails, set inclined at an angle 9 to the horizontal as shown in figure-5.30.
 The top end of the bar are connected with a capacitor of capacitance C. The system is placed in a uniform magnetic field, in the direction perpendicular to the inclined plane formed by the rails as shown in figure. If the resistance of the bars and the sliding conductor are negligible calculate the acceleration of sliding conductor as a function of time ifit is released from rest at t= 0
The top end of the bar are connected with a capacitor of capacitance C. The system is placed in a uniform magnetic field, in the direction perpendicular to the inclined plane formed by the rails as shown in figure. If the resistance of the bars and the sliding conductor are negligible calculate the acceleration of sliding conductor as a function of time ifit is released from rest at t= 0
View Solution
Knowledge Check
A small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __
 AThen the end X of the rod becomes positively chargedBThe end Y of the rod becomes positively chargedCThe entire rod is unevenly chargedDThe rod becomes hot due to joule heating
AThen the end X of the rod becomes positively chargedBThe end Y of the rod becomes positively chargedCThe entire rod is unevenly chargedDThe rod becomes hot due to joule heatingA conducting rod of length l is falling with a velocity v perpendicular to a uniform horizontal magnetic field B. The potential difference between the two ends will be
A2 BlvBBlvC12BlvD12Bl2v2A copper wire ab of length l, resistance r and mass m start sliding at t=0 down a smooth, vertical, thick pair of connected conducting rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct .
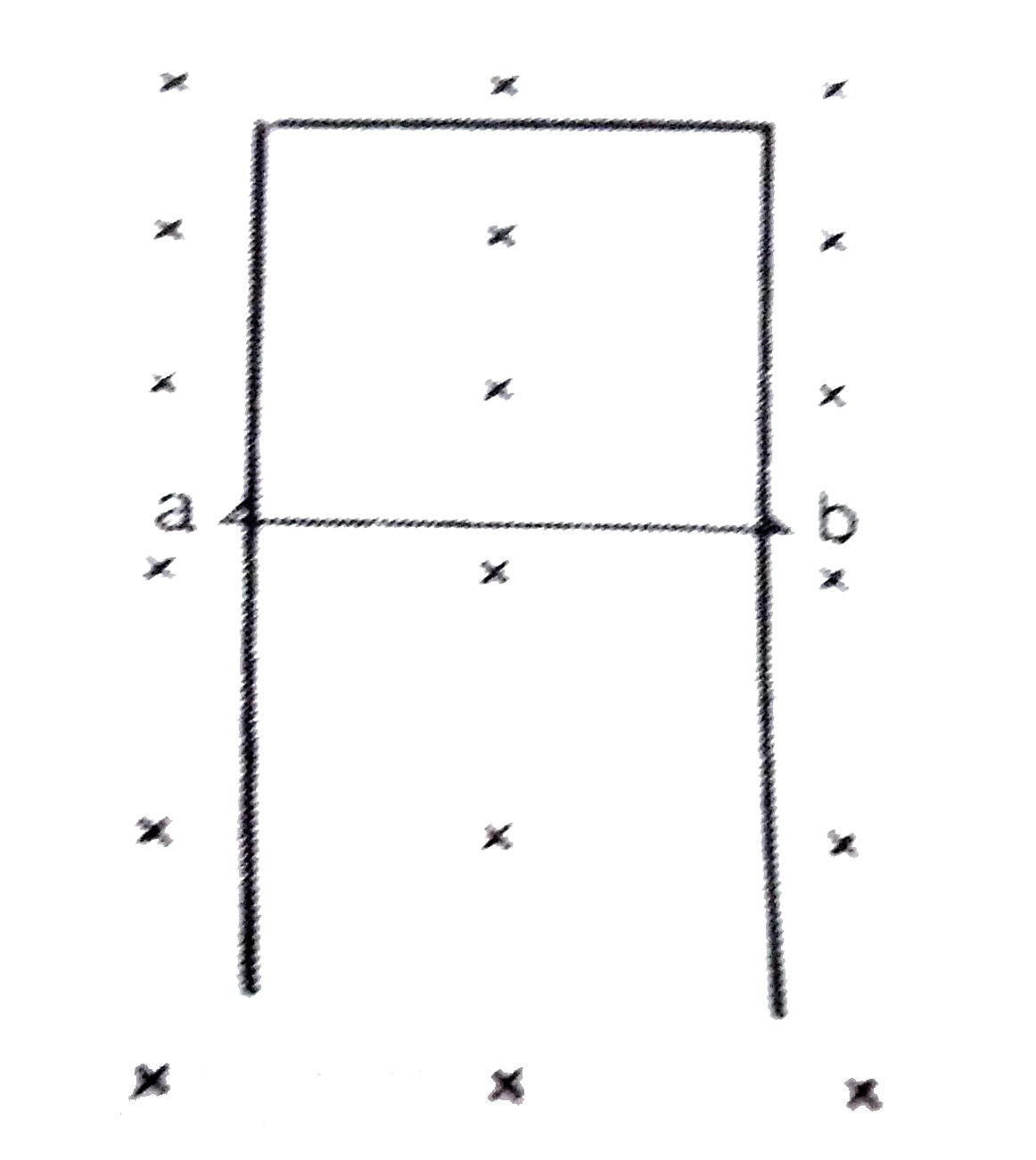 AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrvCThe velocity of the wire as a function of time vm(1−e−gt/vm),(wherevm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm),(wherevm=mgrB2l2)
AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrvCThe velocity of the wire as a function of time vm(1−e−gt/vm),(wherevm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm),(wherevm=mgrB2l2)
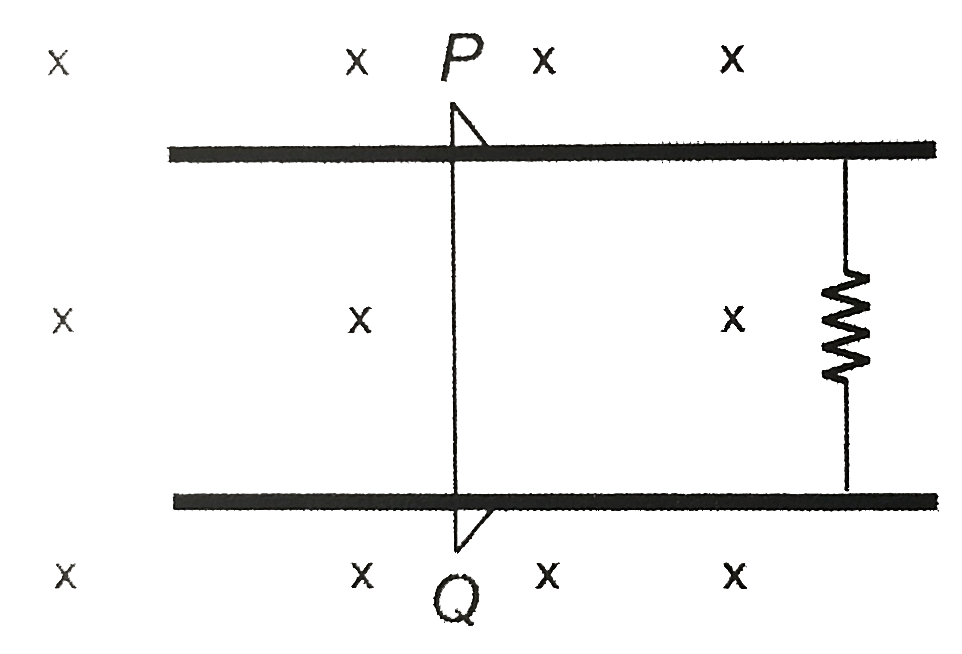
Consider the situation shown in the figure. The wire PQ has mass m , resistance r and can slide 0n the smooth, horizontal parallel rails separated by a distance l . The resistance of the rais is negiligible. A uniform magnetic field B exists in the reactangular region and a resistance R connects the rail outside the field region. At t=0 , the wire PQ is pushed toward right with a speed v0 . Find
(a) the current in the loop at an instant when the speed of the wire PQ is v
(b) the acceleration of the wire as this instant
(c) the velocity v as a function of x
(d) the maximum distance the wire will move
(e) the velocity as a function of time
View SolutionFigure showns a smooth pair of thick metallic rails connected across a battery of emfε having a negligible internal resistance.A wire ab of length l and resistance r can slide smoothly on the rails.The entire system lies in a horizontal plane and is immersed in a uniform vertical magnetic field B.At an instant t the wire at this instant. (b)What is the force acting on the wire at this instant. (c)Show that after some time the wire ab will slide with a constant velocity.Find this velocity.
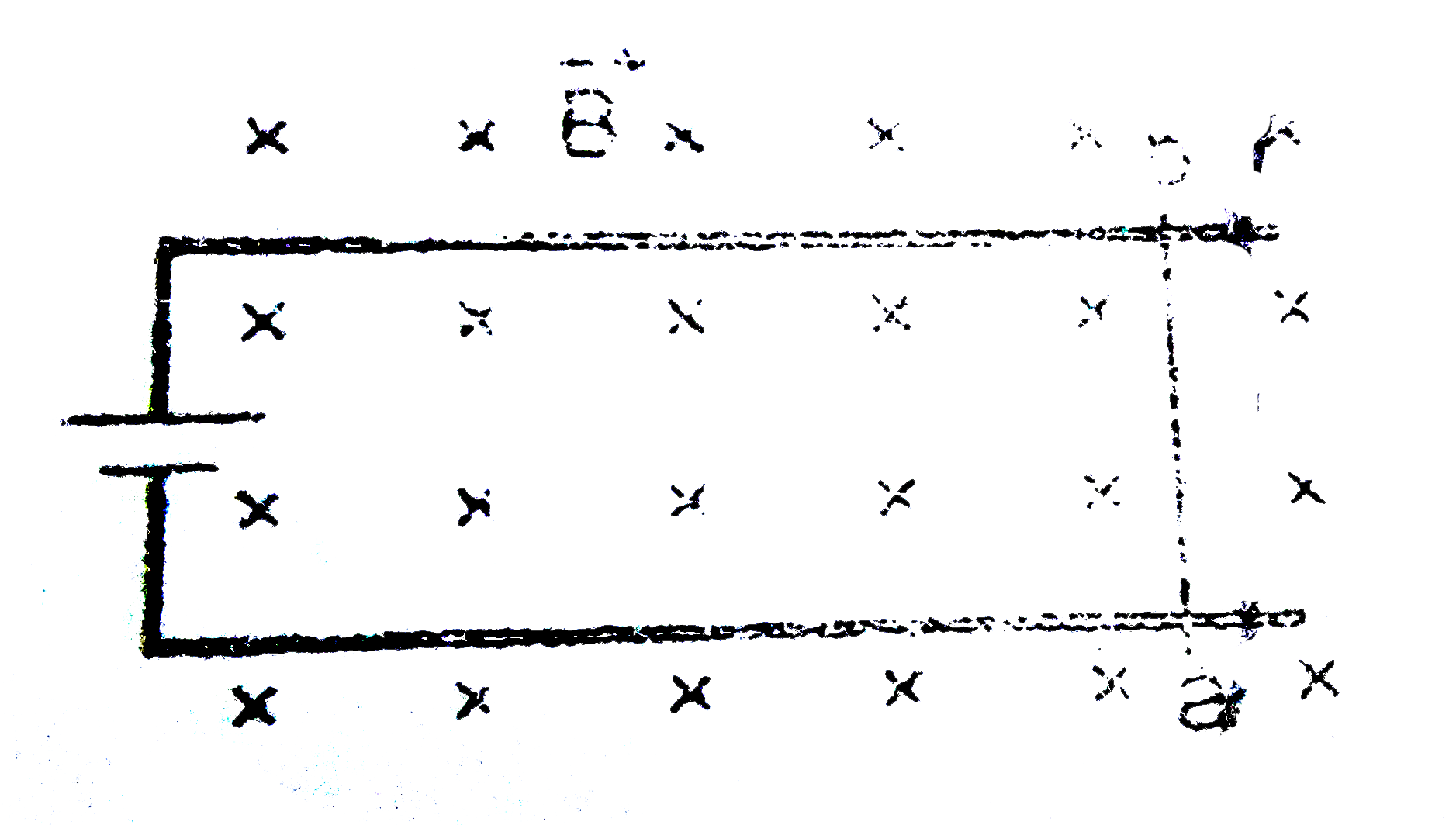
View SolutionA copper wire ab of length l, resistance r and mass m starts sliding at t=0 down a smooth, vertical, thick pair of connected condcuting rails as shown in figure.A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct.
View SolutionA conducting rod of length l and mass m is moving down a smooth inclined plane of inclination θ with constant i is flowing in the conductor in a direction perpendicular to paper inwards. A vertically upward magnetic field →B exists in space. Then, magnitude of magnetic field →B is

View SolutionA conducting rod of length l and mass m is moving down a smooth inclined plane of inclination θ with constant velocity V as shown in figure. A current I is flowing in the conductor in a direction perpendicular to paper inwards. Let a vertically upward magnetic field →B be existent in space. Then, what is the magnitude of magnetic field →B?
View Solution
