A rough horizontal plate rotates with a constant angular velocity w about its vertical axis. A particle of mass m lies on the plate at a distance 5a4 from the axes. If the coefficient of friction is 13 and the particle remains at rest relative to the plane, show that w≤√4g15a. The particle is now connected to axis by a horizontal elastic string, of natural length a and modulus 3 mg. If the particle remains at rest relative to the plate and at a distance 5a4, show that the greatest possible angular velocity is √1315.ga and find the least possible velocity.
The correct Answer is:√13.ga
Step by step video, text & image solution for A rough horizontal plate rotates with a constant angular velocity w about its vertical axis. A particle of mass m lies on the plate at a distance (5a)/(4) from the axes. If the coefficient of friction is (1)/(3) and the particle remains at rest relative to the plane, show that w le sqrt((4g)/(15a)). The particle is now connected to axis by a horizontal elastic string, of natural length a and modulus 3 mg. If the particle remains at rest relative to the plate and at a distance (5a)/(4), show that the greatest possible angular velocity is sqrt((13)/(15).(g)/(a)) and find the least possible velocity. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRIPITAL AND CENTRIFUGAL FORCESBook:NN GHOSHChapter:CENTRIPITAL AND CENTRIFUGAL FORCESExercise:Exercises (A)
Explore 18 Videos
- CALORIMETRYBook:NN GHOSHChapter:CALORIMETRYExercise:All Questions
Explore 28 Videos
- COMPOSITION AND RESOLUTION OF VELOCITIESBook:NN GHOSHChapter:COMPOSITION AND RESOLUTION OF VELOCITIESExercise:Exercise
Explore 25 Videos
Similar Questions
A particle of mass m is placed over a horizontal circular table rotating with an angular velocity ω about a vertical axis passing through its centre. The distance of the object from the axis is r. Find the force of friction f between the particle and the table.
View SolutionA smooth horizontal disc rotates about the vertical axis O (figure) with a constant angular velocity ω. A thin uniform rod AB of length l performs small oscillation about the vertical axis A fixed to the disc at a distance a from the axis of the disc. Find the frequency ω0 of these oscillations.

View Solution
Knowledge Check
A rough horizontal plate rotates with angular velocity ω about a fixed verticle axis. A particle or mass m lies on the plate at a distance 5a4 from this axis. The coefficient of friction between the plate and the particle is 13 . The largest value of ω2 for which the oparticle will continue to be at rest on the revolving plate is
Ag3aB4g5aC4g9aD4g15aA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A circular plate is rotating about its own axis at an angular velocity 100 revolutions per minute. The linear velocity of a particle P of plate at a distance 4.2cm from axis of rotation is
A0.22m/sB0.44m/sC2.2m/sD4.4m/s
A particle of weight W rests on a rough inclined plane which makes an angle α with the horizontal . If the coefficient of static friction μ=2tanα , find the horizontal force H acting transverse to the slope of the plane when the particle is about to slip :

View SolutionA circular of radius 20 cm is rotating about its own axis at an angular velocity ω . The angular velocity of a particle 'A' which is at a distance 10 cm from the axis of rotation is
View SolutionA particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
View SolutionA uniform rod of length l and mass M rotating about a fixed vertical axis on a smooth horizontal table. It elastically strikes a particle placed at a distance l/3 from its axis and stops. Mass of the particle is -
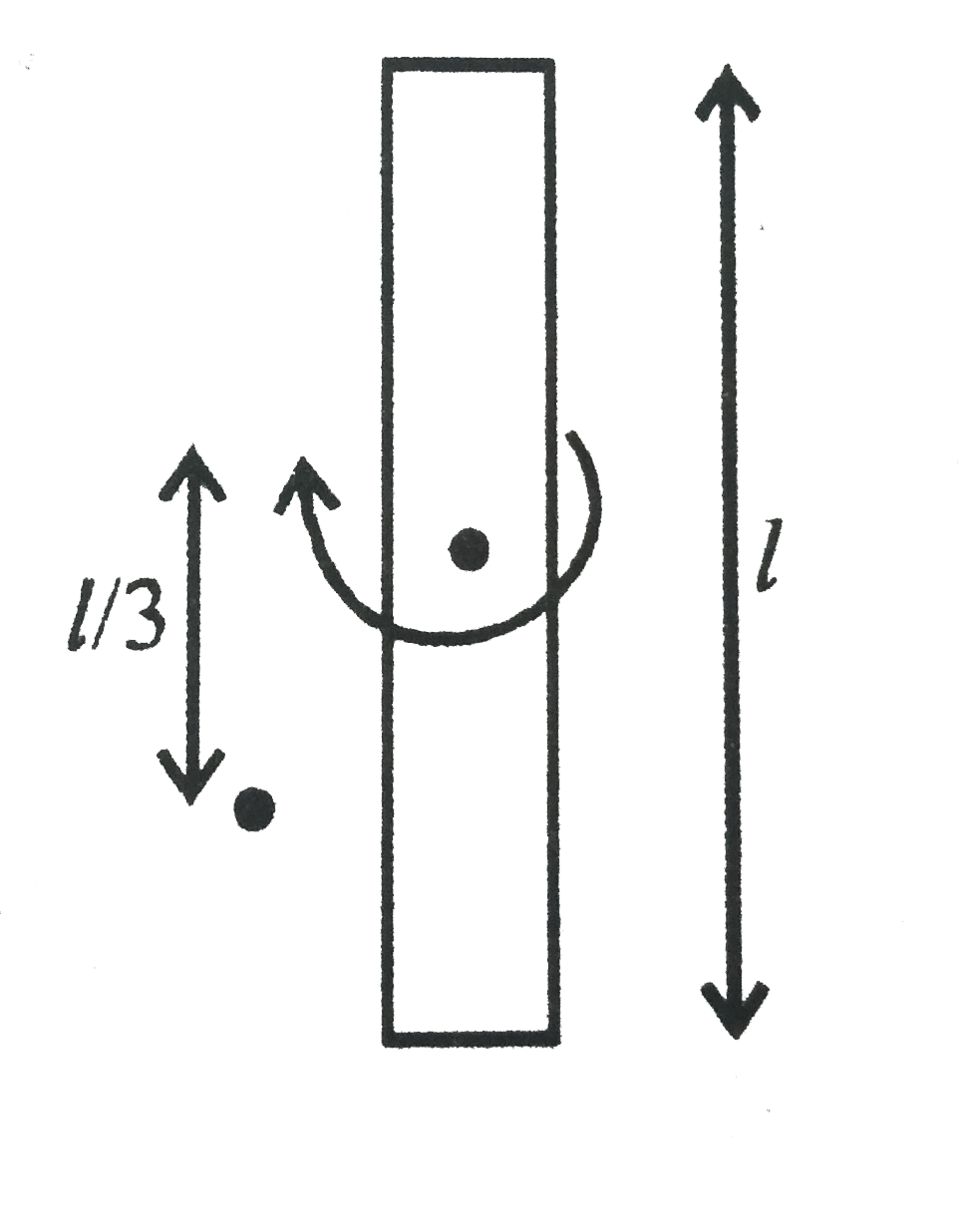 .
.
View SolutionA rigid body of mass m rotates with angular velocity ω about an axis at a distance a from the centre of mass G. The radius of gyration about a parallel axis through G is k. The kinetic energy of rotation of the body is
View Solution
