A round dielectric disc of radius R and thickness d is statically polarized so that it gains the uniform polarzation P. With the vector P lying in the plane of the disc. Find the strength E of the electric field at the centre of the disc if d<<R.
Because there is a discontinuity in polarization at the boundary of the dielectric disc, a bound surface charge appears, which is the source of the electric field inside and outside the disc.
We have for the electric field at the origin.
→E=−∫σdS4πε0r3→r,
where →r = radius vector to the origin form the element dS.
σ'=Pn=Pcosθ on the curved surface (Pn=0 on the flat surface.)
Here θ = angle between →r and →P
By symmetry, →E will be parallel to →P. Thus
E=−∫2x0PcosθRdθcosθ4πε0R2.d
where, r=R it d<<R.
So, E=−Pd4ε0R and →E=−→Pd4ε0R

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field46videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current72videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field36videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
At which distance along the centre axis of a uniformaly charged plastic disc of radius R is the magnitude of the electric field equal to one-half the magnitude of the field at the centre of the surface of the disc ?
View SolutionAn infinielty long round dielectric cyclinder is polarized uniformly and statically, the polarization P being perpendicular to the axis of the cyclinder. Find the electric field strength E inside teh dielectric.
View Solution
Knowledge Check
- Question 1 - Select One
At which distance along the centre axis of a uniformaly charged plastic disc of radius R is the magnitude of the electric field equal to one-half the magnitude of the field at the centre of the surface of the disc ?
AR√2BR√3C√2RD√3R - Question 2 - Select One
Find the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
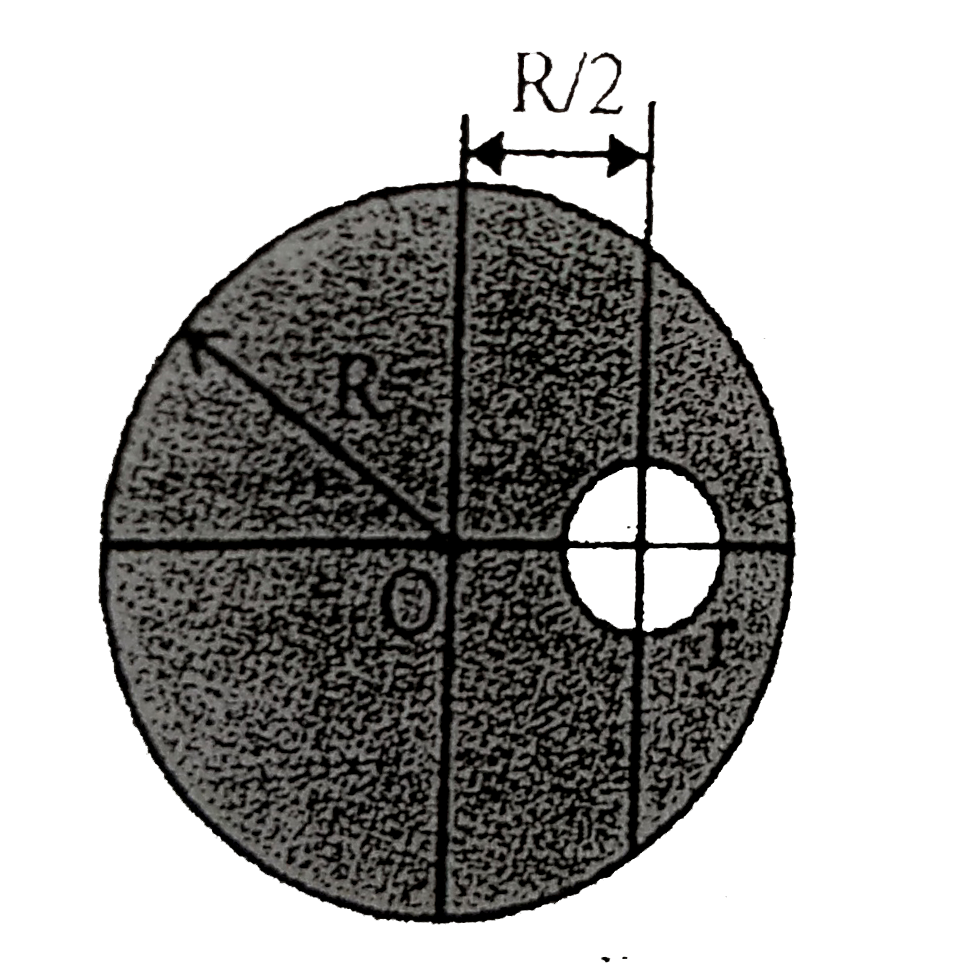 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
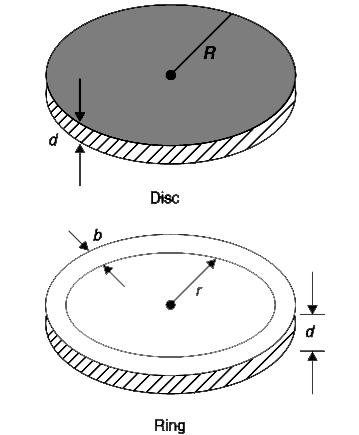
A steel ring is to be fitted on a wooden disc of radius R and thickness d. The inner radius of the ring is r which is slightly smaller than R. The outer radius of the ring is r + b and its thickness is d (same as the disc). There is no change in value of b and d after the ring is fitted over the disc, only the inner radius becomes R. If the Young’s modulus of steel is Y, calculate the longitudinal stress developed in it. Also calculate the tension force developed in the ring.
[Take b<<r]
 View Solution
View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View SolutionA plate of thickness h made of uniform statically polarized dielectric is placed inside a capacitor whose parallel plates are interconnected by a conductor. The polarization of the dielectric is equal

to P (Fig). The separation between the capacitor plates is d. Find teh strength and induction vectors for the electric field both inside and outside the plates.View SolutionA conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA conducting disc of radius r rotaes with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View Solution

