An infinite plane of uniform dielectric with permittivity ε is uniformly charged with extraneous chagre fo space density ρ. The thickness of the plate is equal to 2d. Find:
(a) the magnitude of the electric field strength and the potential as functions of distance l from the middle point of the plane.(where the potential is assumed to be equal to zero), having chosen teh x coriditnate axis perpendicular to the plate, draw the approximate plots of teh projection Ex(x) of the vector E and the potentail φ(x), plots fo the projection Ex(x) of the vector E adn the potential φ(x),
(b) the surface and space denstites of the bound charge.
(a) div →D=∂D∂x=ρ and D=ρl
Ex=ρlεε0,l<d and Ex=ρdε0 constant for l>d.
φ(x)=−ρl22εε0,l<d and φ(x)=A−ρldε0,l>d then φ(x)=ρdε0(d−d2e−t), by continuity.
On the basic of obtained expressions Ex(x) and φ(x) can be plotted as shown in fig of answersheet.
(b) ρ'=−div →p=−div (ε−1)ε0→E=−ρ(ε−1)ε
σ'=P1n−P2n, where n is the normal from 1 to 2.
P1n, (→p2=0 as 2 is vacumm.)
=(ρd−ρd/ε)=ρdε−1ε
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field
46 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current
72 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field
36 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
Half the space between two concentricv elecrodes of a sphereical capacitor is filled , as shwon in Fig, with unifrom istropic dielectric with permittively ε. The charge of the capacitor is q. Find the magnitude of the electric field strength between teh electrodes as a function of distance r from the curvature centre of teh electrodes.
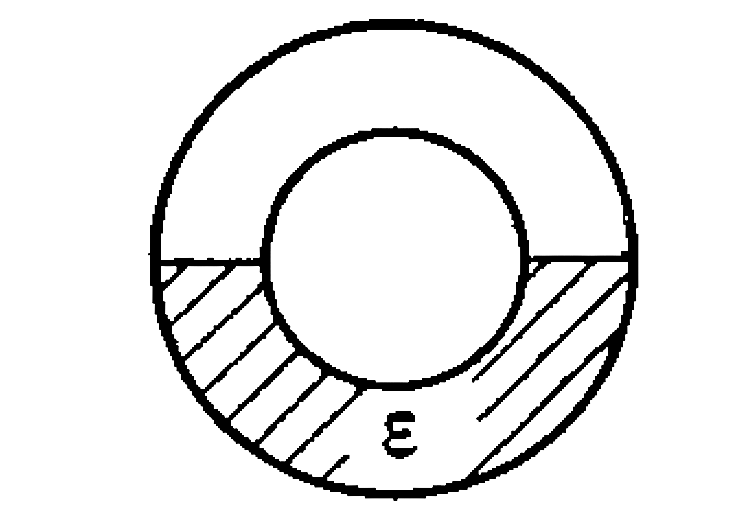
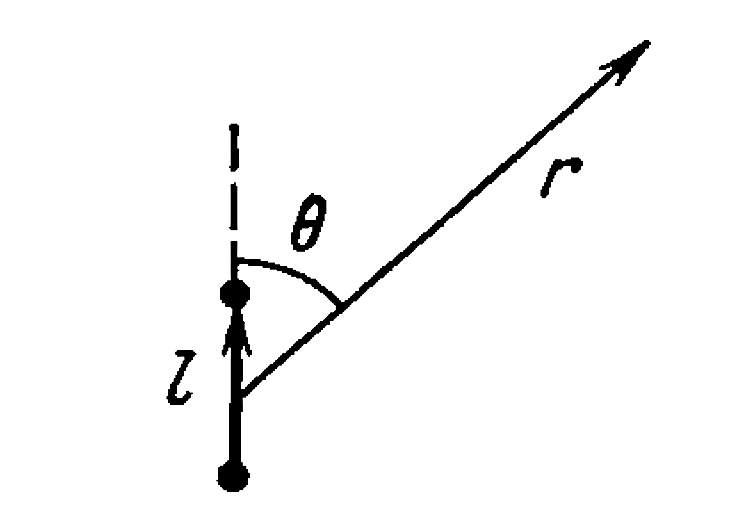
View SolutionTwo this parallel threads carry a uniform charge with linear densities lamnda and −λ . The distance between the threads is equal to l. Find the potential of the electric field and the magnitude of its strength vector at the distance r>>l at the angle θ to the vector 1 (fig).
View Solution
Knowledge Check
In a certain region of space the electric potential V is known to be constant. Is the electric field in this region (a) positive (b) zero ,or (c ) negative ?
AAlso constantBPositiveCNegativeDZeroThe expression for electric field intensity at a points outside uniformly charged thin plane sheet is (where, d is the distance of point from plane sheet)
Aindependent of dBdirectly proportional to √dCdirectly proportional to dDdirectly proportional to 1√d
Extraneous chagres are uniformly distributed with space density ρ>0 over a ball of radius R made of uniform istropis dielectric with permittivity ε. Find :
(a) magnitude of the electric field strength as a function of distance r from the centre of the ball, draw teh approixmate plots E(r) adn φ(r),
(b) the space and surface densities of the bound charges.
View SolutionA ball of radius R is uniformly charged with the volume density ρ. Find the flux if the electric field strength vector across the balls section formed by the plane located at a distance r0<R from the centre of the ball.
View SolutionFind the potential due to an infinite sheet of charge at a distance x from it. Assume that the potential is zero at a distance a from it.
View SolutionA half-space filled with uniform istropic dielectrics with permittivity ε has the conducting boundary plane. Inside the dielectric at a distance l from this plane, there is a small metal ball possensing a charge q. Find the surface density of the bound chagres at the boundary plane as a function plane as a function of distance r from the ball.
View SolutionA nonconducting sheet of large surface area and thickness d contains uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane.
View SolutionA point charge q si located on the plane dividing vacumm and infinite uniform istropic dielectric with permittivity eposilon. Find the moduli of the vectors D and E as well as the potentail φ as funtions of distance r from the charge q.
View Solution
