Question

A satellite is to be put into an orbit $600km$ above the surface of the earth. If its vertical velocity after launching is $2400m/s$ at this height, calculate the magnitude and direction in the impulse required to put the satellite directly increase. The mass of the satellite is $60kg$ and the radius of the earth is $6400km$. Take $g=10m{s}^{-2}$

Answer

Impulse `4.77xx10^(5)m//s` at an angle `tan^(-1)(0.317)` from horizontal (downward)

Explanation

Orbital velocity
`v_(0)=sqrt((GM)/r)=sqrt((R^(2)g)/r)`
`v_(0)=sqrt({((6400xx10^(3))^(2)xx9.8)/(7000..10^(3))})=7572.6ms^(-1)`

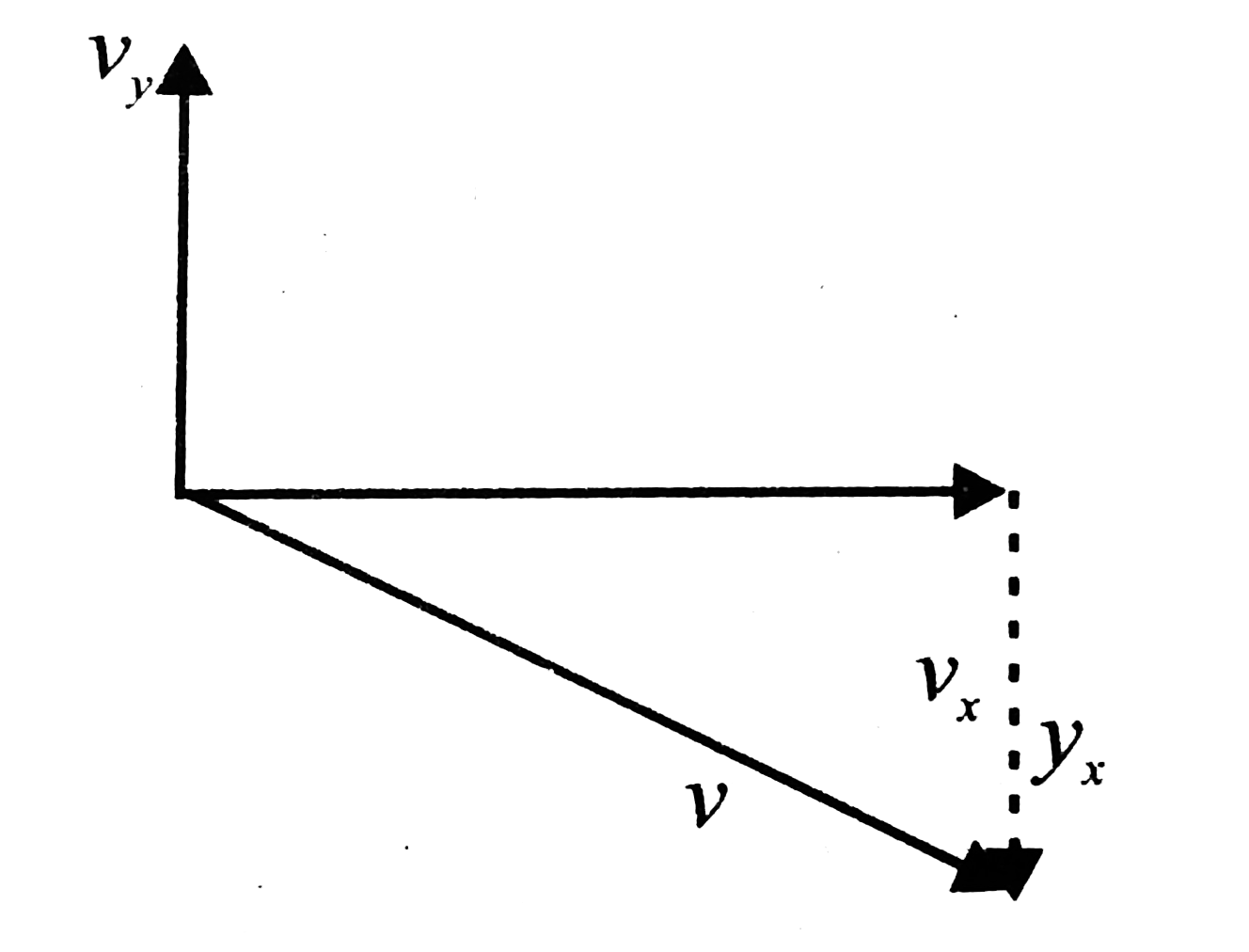
This velociyt is horizontal so`v_(0)=v_(x)=7572.6ms^(-1)`
for launching the satellite in the circular orbit, the vertical component of velocity should be zero, so the velocity required is
`v_(x)=7572.25ms^(-1)` and `v_(y)` (downward)=`2400ms^(-1)`
Therefore the required impulse is
`sqrt((mv_(x))^(2)x(mv_(3))^(2))=msqrt(v_(x)^(2)+v_(x)^2)`
`=60sqrt((572.6)^(2)+(2400)^(2))`
`=4.7xx10^(5)kgm^(1)`
`tantheta=(v_(y))/(v_(x))=2400-7572.6-0.317`
`theta=tan^(-1)(0.317)=17.6^@`
Hence impulse`=4.77xx10^(5)ms^(-1)` at an angle `17.6^@` from horizontal downward.