A satellite needs no fuel to move round a planet in a stable orbit. Why?
To understand why a satellite needs no fuel to move around a planet in a stable orbit, we can break down the explanation into several steps:
1. Understanding Satellite Motion:
A satellite orbits a planet due to the gravitational force exerted by the planet. This gravitational force acts as the centripetal force that keeps the satellite in its circular path.
2. Direction of Forces:
The gravitational force acts towards the center of the planet, while the satellite is moving tangentially to its orbit. This means that the direction of the gravitational force is perpendicular to the direction of the satellite's motion.
3. Centripetal Force:
The gravitational force provides the necessary centripetal force required for the satellite to maintain its circular orbit. Since this force is always directed towards the center of the planet, it does not do any work on the satellite.
4. Work Done by Forces:
Work done is defined as the product of force and displacement in the direction of the force. Since the gravitational force (centripetal force) is perpendicular to the displacement of the satellite, the work done by this force is zero.
5. No Need for Fuel:
Because the work done by the gravitational force is zero, the satellite does not lose energy while in orbit. Therefore, it does not require any fuel to maintain its motion in a stable orbit.
Final Conclusion:
A satellite needs no fuel to move around a planet in a stable orbit because the gravitational force acting on it provides the necessary centripetal force without doing any work, allowing the satellite to maintain its motion indefinitely.
A satellite orbits a planet due to the gravitational force exerted by the planet. This gravitational force acts as the centripetal force that keeps the satellite in its circular path.
The gravitational force acts towards the center of the planet, while the satellite is moving tangentially to its orbit. This means that the direction of the gravitational force is perpendicular to the direction of the satellite's motion.
The gravitational force provides the necessary centripetal force required for the satellite to maintain its circular orbit. Since this force is always directed towards the center of the planet, it does not do any work on the satellite.
Work done is defined as the product of force and displacement in the direction of the force. Since the gravitational force (centripetal force) is perpendicular to the displacement of the satellite, the work done by this force is zero.
Because the work done by the gravitational force is zero, the satellite does not lose energy while in orbit. Therefore, it does not require any fuel to maintain its motion in a stable orbit.
A satellite needs no fuel to move around a planet in a stable orbit because the gravitational force acting on it provides the necessary centripetal force without doing any work, allowing the satellite to maintain its motion indefinitely.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - GRAVITATIONEXERCISE - LONG ANSWER QUESTIONS13videos
GRAVITATION
- BOOK - ICSECHAPTER - GRAVITATIONEXERCISE - SHORT ANSWER QUESTIONS27videos
GRAVITATION
- BOOK - ICSECHAPTER - GRAVITATIONEXERCISE - ADDITIONAL SOLVED PROBLEMS15videos
GRAVITATION
- BOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems30videos
FRICTION
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM HEAT ENGINES)21videos
INTERNAL ENERGY
Similar Questions
A satellite revolves around a planet in a circular orbit. What is the work done by the satellite at any instant ? Give a reason.
View SolutionWhich of the following statements are correct about a satellite moving around a planet in an elliptical orbit ?
View SolutionTwo satellites A and B move round the earth in the same orbit. The mass of B is twice the mass of A.
View SolutionA satellite revolve round a planet in an orbit just above the surface of a planet. Taking G=6.67×10−11Nm2kg2 and mean density of the planet 5.51×103kg/m3 find the period of the planet.
View SolutionA light satellite is initially rotating around a planet in a circular orbit of radius r. Its speed in this circular orbit was u0. It is put in an elliptical orbit by increasing its speed form u0 to vQ ( instantaneously). In the elliptical orbit, the satellite reaches the farthest point P, which is at a distance R from the planet. Satellite's speed at farthest point is vP. At point Q, the speed required by satellite to escape the planet's gravitational pull is vesc
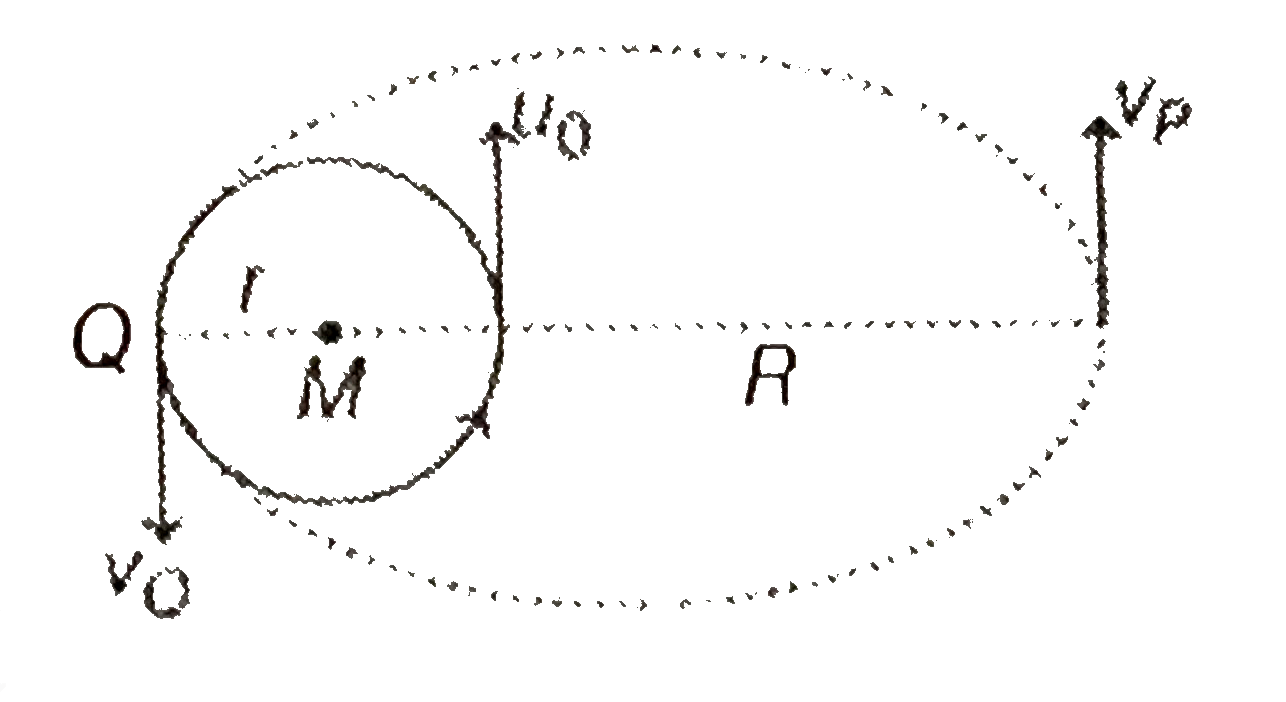 View Solution
View SolutionA small satellite revolves round a planet in an orbit just above planet's surface. Taking the mean density of planet as ρ, calculate the time period of the satellite.
View SolutionThe orbital speed of a satellite revolving around a planet in a circular orbit is v0 . If its speed is increased by 10 % ,then
View SolutionA small satellite revolves around a planet in an orbit just above planet's surface. Taking the mean density of the planet 8000kgm−3 and G=6.67×10−11N/kg−2, find the time period of the satellite.
View SolutionA satellite X moves round the earth in a circular orbit of radius R. If another satellite Y of the same mass moves round the earth in a circular orbit of radius 4R, then the speed of X is ____________ times that of Y.
View SolutionA satellite is in an elliptical orbit around a planet P. It is observed that the velocity of the satellite when it is farthest from the planet is 6 times less than that when it is closest to the planet . The ratio of distances between the statellite and the planet at closest and farthest points is :
View Solution

