The orbital speed of a satellite revolving around a planet in a circular orbit is v0 . If its speed is increased by 10 % ,then
It will escape from its orbit
It will start rotating in an elliptical
It will continue to move in the same orbit
It will move in a circular orbit of radius 20 % more than radius of intial orbit
The correct Answer is:B
To solve the problem, we need to analyze the effects of increasing the orbital speed of a satellite by 10%.
1. Understanding Orbital Speed:
The orbital speed v0 of a satellite in a circular orbit is given by the formula:
v0=√GMr
where G is the gravitational constant, M is the mass of the planet, and r is the radius of the orbit.
2. Increasing the Speed:
If the speed is increased by 10%, the new speed v can be expressed as:
v=v0+0.1v0=1.1v0
3. Centripetal Force and Gravitational Force:
For a satellite in orbit, the centripetal force required to keep it in circular motion is provided by the gravitational force. The centripetal force Fc is given by:
Fc=mv2r
The gravitational force Fg acting on the satellite is:
Fg=GMmr2
4. Setting Up the Equation:
Initially, at speed v0:
mv20r=GMmr2
This shows that the centripetal force equals the gravitational force.
5. Substituting the New Speed:
Now, substituting v=1.1v0 into the centripetal force equation:
F′c=m(1.1v0)2r=m(1.21v20)r
6. Comparing Forces:
The new centripetal force becomes:
F′c=1.21⋅mv20r
Since we know that mv20r=GMmr2, we can substitute:
F′c=1.21⋅GMmr2
This indicates that the new centripetal force F′c is greater than the gravitational force Fg.
7. Conclusion:
Since the centripetal force F′c exceeds the gravitational force Fg, the satellite will no longer be able to maintain its orbit and will escape. Therefore, the correct conclusion is that the satellite escapes from its orbit.
Final Answer:
The satellite escapes from its orbit.
The orbital speed v0 of a satellite in a circular orbit is given by the formula:
v0=√GMr
where G is the gravitational constant, M is the mass of the planet, and r is the radius of the orbit.
If the speed is increased by 10%, the new speed v can be expressed as:
v=v0+0.1v0=1.1v0
For a satellite in orbit, the centripetal force required to keep it in circular motion is provided by the gravitational force. The centripetal force Fc is given by:
Fc=mv2r
The gravitational force Fg acting on the satellite is:
Fg=GMmr2
Initially, at speed v0:
mv20r=GMmr2
This shows that the centripetal force equals the gravitational force.
Now, substituting v=1.1v0 into the centripetal force equation:
F′c=m(1.1v0)2r=m(1.21v20)r
The new centripetal force becomes:
F′c=1.21⋅mv20r
Since we know that mv20r=GMmr2, we can substitute:
F′c=1.21⋅GMmr2
This indicates that the new centripetal force F′c is greater than the gravitational force Fg.
Since the centripetal force F′c exceeds the gravitational force Fg, the satellite will no longer be able to maintain its orbit and will escape. Therefore, the correct conclusion is that the satellite escapes from its orbit.
The satellite escapes from its orbit.
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS)
51 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - A (OBJECTIVE TYPE QUESTIONS)
41 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
Knowledge Check
A satellite is moving around the earth with speed v in a circular orbit of radius r. IF the orbit radius is decreased by 1%, its speed will
Aincrease by 1%Bincrease by 0.5 %Cdecrease by 1%Ddecrease by 0.5 %A satellite is orbiting the earth in a circular orbit of radius r. Its
AKnetic enegy varies as rBangular momentum varies as 1√rClinear momentum varies as 1rDfrequency of revolution varies as 1r3/2An earth satellite is moving around the earth in circular orbit. IN such case what is conserved
AvelocityBlinear momentumCangular momentumDnone of the above
The orbital speed of geostationary satellite is around
View SolutionIf L is the angular momentum of a satellite revolving around earth is a circular orbit of radius r with speed v , then
View SolutionA satellite is revolving around a planet in a circular orbit. What will happen, if its speed is increased from υ0 to
(a) √1.5υ0 (b) 2υ0
View SolutionA satellite revolves around a planet in a circular orbit. What is the work done by the satellite at any instant ? Give a reason.
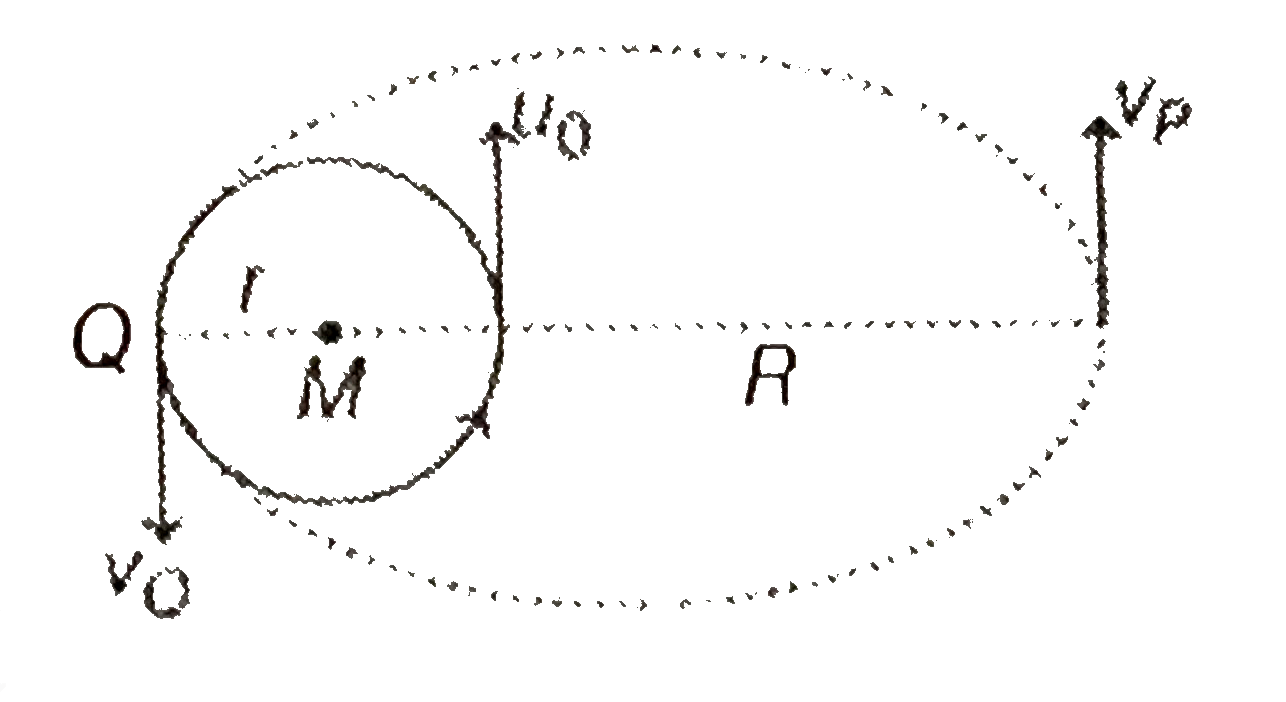
View SolutionA light satellite is initially rotating around a planet in a circular orbit of radius r. Its speed in this circular orbit was u0. It is put in an elliptical orbit by increasing its speed form u0 to vQ ( instantaneously). In the elliptical orbit, the satellite reaches the farthest point P, which is at a distance R from the planet. Satellite's speed at farthest point is vP. At point Q, the speed required by satellite to escape the planet's gravitational pull is vesc
View Solution
