A series combination of N1 capacitors (each of capacity C1) is charged to potential difference 3V. Another parallel combination of N2 capacitors (each of capacity C2) is charged to potential difference V. The total energy stored in both the combinations is same, The value of C1 in terms of C2 is
C2N1N29
C2N21N229
C2N19N2
C2N29N1
The correct Answer is:A
Step by step video, text & image solution for A series combination of N_(1) capacitors (each of capacity C_(1)) is charged to potential difference 3V. Another parallel combination of N_(2) capacitors (each of capacity C_(2)) is charged to potential difference V. The total energy stored in both the combinations is same, The value of C_(1) in terms of C_(2) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - EVALUATION TEST14videos
ELECTROSTATICS
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - CRITICAL THINKING67videos
ELECTROSTATICS
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EVALUATION TEST8videos
ELECTROMAGNETIC INDUCTION
- BOOK - TARGET PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EVALUATION TEST24videos
GRAVITATION
Similar Questions
A series combination of 5 capacitors, each of capacitance 1μF,is charged by a source of potential difference 2V. When another parallel combination of 10 capacitors each of capacitance C2 ,is charged by a source of potential difference V ,it has the same total energy stored in it as the first combination has.The value of C2 is
View SolutionSketch a graph to show how charge Q given to a capacitor of capacity C varies with the potential difference V.
View Solution
Knowledge Check
- Question 1 - Select One
A series combination of n1 capacitors, each of value C1, is charged by a source of potential difference 4V. When another parallel combination of n2 capacitors, each of value C2, is charged by a source of potential difference V, it has same (total) energy stored in it, as the first combination has. the value of C2, in terms of C1, is then
A2C1n1n2B16n2n1C1C2n2n1C1D16C1n1n2 - Question 2 - Select One
A capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
AC(V0−V)VBC(V−V0)VCCVV0DCV0V - Question 3 - Select One
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
Find the ratio of potential difference that must be applied across the parallel and series combination of two capacitors C1andC2 with their capacitance in the ratio 1:3 so that energy stored in the two cases becomes the same.
View SolutionA capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
View SolutionA capacitor of capacity C1 is charged to the potential of V0. On disconnecting with the battery, it is connected with a capacitor of capacity C2 as shown in the adjoining figure. The ratio of energies before and after the connection of switch S will be
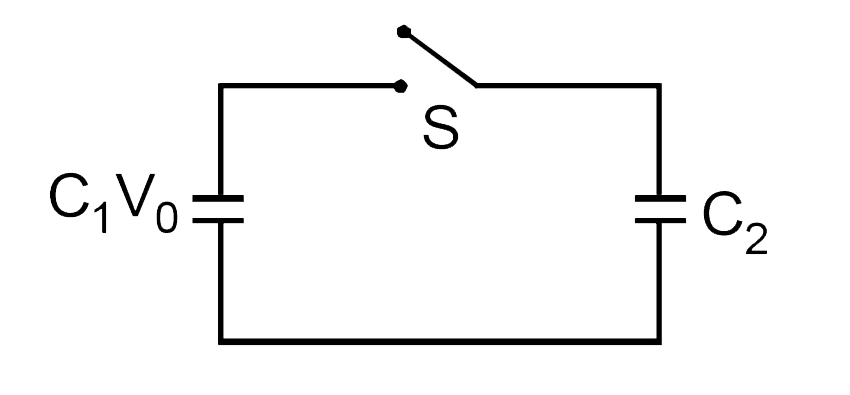 View Solution
View SolutionA capacity of capacity C1 is charged up to V volt and then connected to an uncharged capacitor of capacity C2. Then final potential difference across each will be
View Solutionn capacitors each of capacity C are joined in parallel. If they are connected to a source of V volts, then the energy stored in the capacitor is
View Solution

