The insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
no change in the energy of the system.
no increase in the energy of the system,
always a decrease in the energy of the system
a decrease in the energy of the system unless Q1R2=Q2R1
The correct Answer is:D
Step by step video, text & image solution for The insulated spheres of radii R_(1) and R_(2) having charges Q_(1) and Q_(2) respectively are connected to each other. There is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - EVALUATION TEST14videos
ELECTROSTATICS
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - CRITICAL THINKING67videos
ELECTROSTATICS
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EVALUATION TEST8videos
ELECTROMAGNETIC INDUCTION
- BOOK - TARGET PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EVALUATION TEST24videos
GRAVITATION
Similar Questions
There are two spheres of radii R and 2R having charges Q and Q2 respectively. These two spheres are connected with a cell of emf V volts as shown in figure. When switch is closed, the final charge on sphere of radius 2R is Q+8πε0RVn . Then find the value of n.
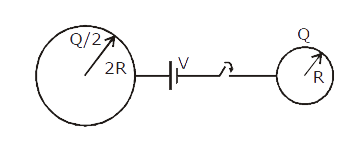 View Solution
View SolutionTwo non-conduction hollow uniformly charged spheres of radil R1 and R2 with charge Q1 and Q2 respectively are places at a distance r. Find out total energy of the system.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two conducting spheres of radii r1 and r2 having charges Q1 and Q2 respectively are connected to each other. There is
Ano change in the energy of the systemBan increase in the energy of the systemCalways a decrease in the energy of the systemDa decrease in the energy of the system unless Q1r2=Q2r1 - Question 2 - Select One
The insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
ANo change in the electrical energy of the systemBAn increase in the electrical energy of the systemCAlways a decrease in the electrical energy of the systemDA decrease in electrical energy of the system until Q1R2=Q2R3 - Question 3 - Select One
Passage III
Two small metallic spheres of radii r1andr2 carry charges q1andq2, respectively such that they have the same polarity. Both the spheres are widely separated from each other and then the two are connected by a metallic wire.
Answer the following questions:
If σ1andσ2 are the corresponding surface charge desities of both the spheres then σ1/σ2 isAr1/r2Br2/r1C2DNone of these
[" Two uniformly charged non "],[" conducting spheres of radii "R_(1)" and "],[R_(2)" having charges "Q_(1)" and "Q_(2)],[" respectively are seperated by "],[" distance "r" .Total electrostatic "],[" energy of this system is "],[qquad [U=(1)/(4 pi epsilon_(0)){(3Q_(1)^(2))/(5R_(1))+(3Q_(2)^(2))/(5R_(2))+(Q_(1)Q_(2))/(r)}],[U=(1)/(4 pi epsilon_(0)){(3Q_(1)^(2))/(5R_(1))+(3Q_(2)^(2))/(5R_(2))-(Q_(1)Q_(2))/(r)}],[U=(1)/(4 pi epsilon_(0)){(Q_(1)^(2))/(5R_(1))+(3Q_(2)^(2))/(5R_(2))-(Q_(1)Q_(2))/(r)}],[U=(1)/(4 pi epsilon_(0)){(3Q_(1)^(2))/(5R_(1))+(3Q_(2)^(2))/(R_(2))+(Q_(1)Q_(2))/(r)}]]
View SolutionThere are two spheres of radii R and 2R having charges Q and Q/2, respectively. These two spheres are connected with a cell of emf V volts as show in. When the switch is closed, find the final charge on each sphere.
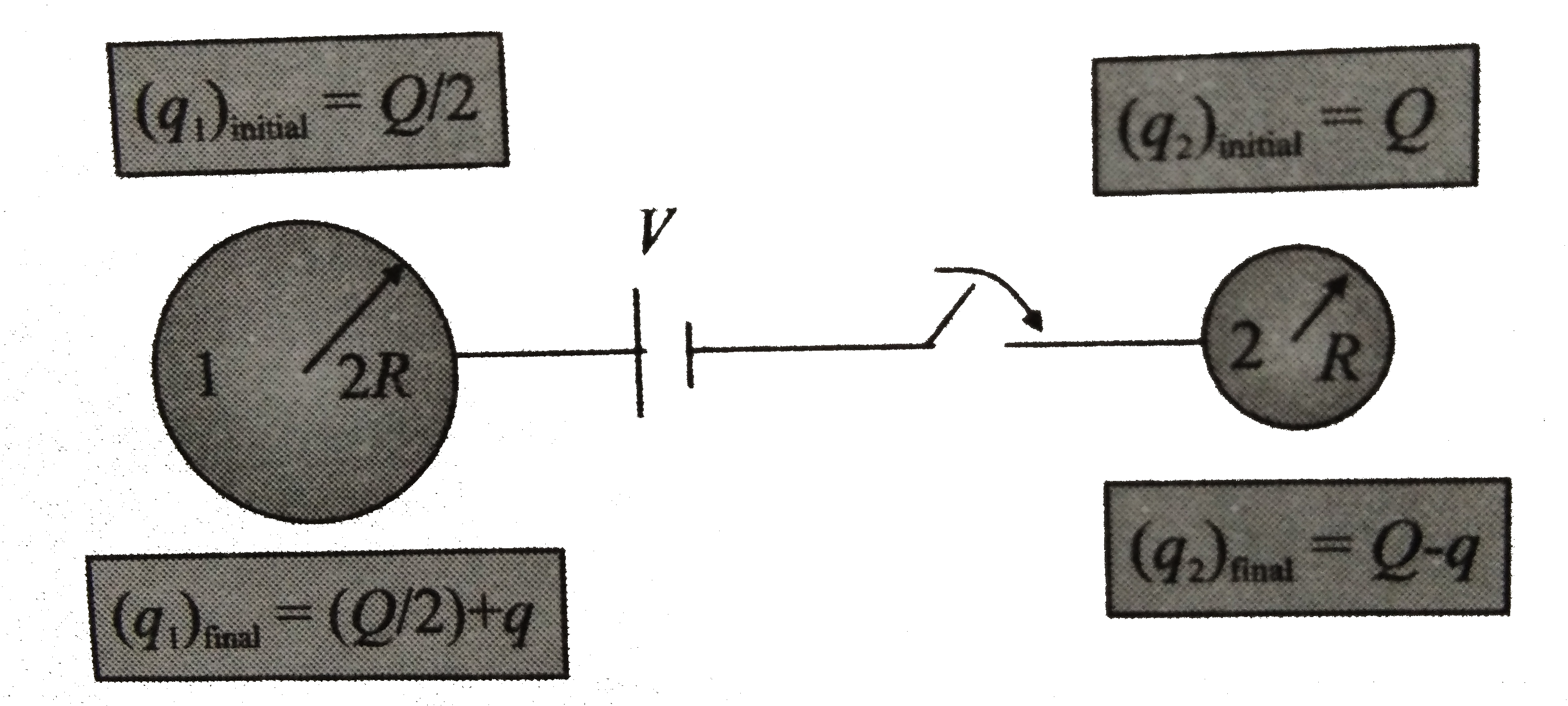 View Solution
View SolutionYou are given two concentric charged conducting spheres of radii R1andR2 such that R1>R2, having charges Q1andQ2 respectively and uniformly distributed over its surface. Calculate E and V at three points A, B , C whose distances from the centre are rA,rBandrc respectively as shown in figure.
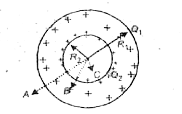 View Solution
View SolutionTwo concentric, thin metallic spheres of radii R1 and R2 (R1>R2) bear charges Q1 and Q2 respectively. Then the potential at distance r between R1 and R_(2) will be
View SolutionFind force acting between two shells of radius R1 and R2 which have uniformly distributed charges Q1 and Q2 respectively and distance between their centres is r.
 View Solution
View Solution

