A series combination of n1 capacitors, each of value C1, is charged by a source of potential difference 4V. When another parallel combination of n2 capacitors, each of value C2, is charged by a source of potential difference V, it has same (total) energy stored in it, as the first combination has. the value of C2, in terms of C1, is then
2C1n1n2
16n2n1C1
2n2n1C1
16C1n1n2
The correct Answer is:D
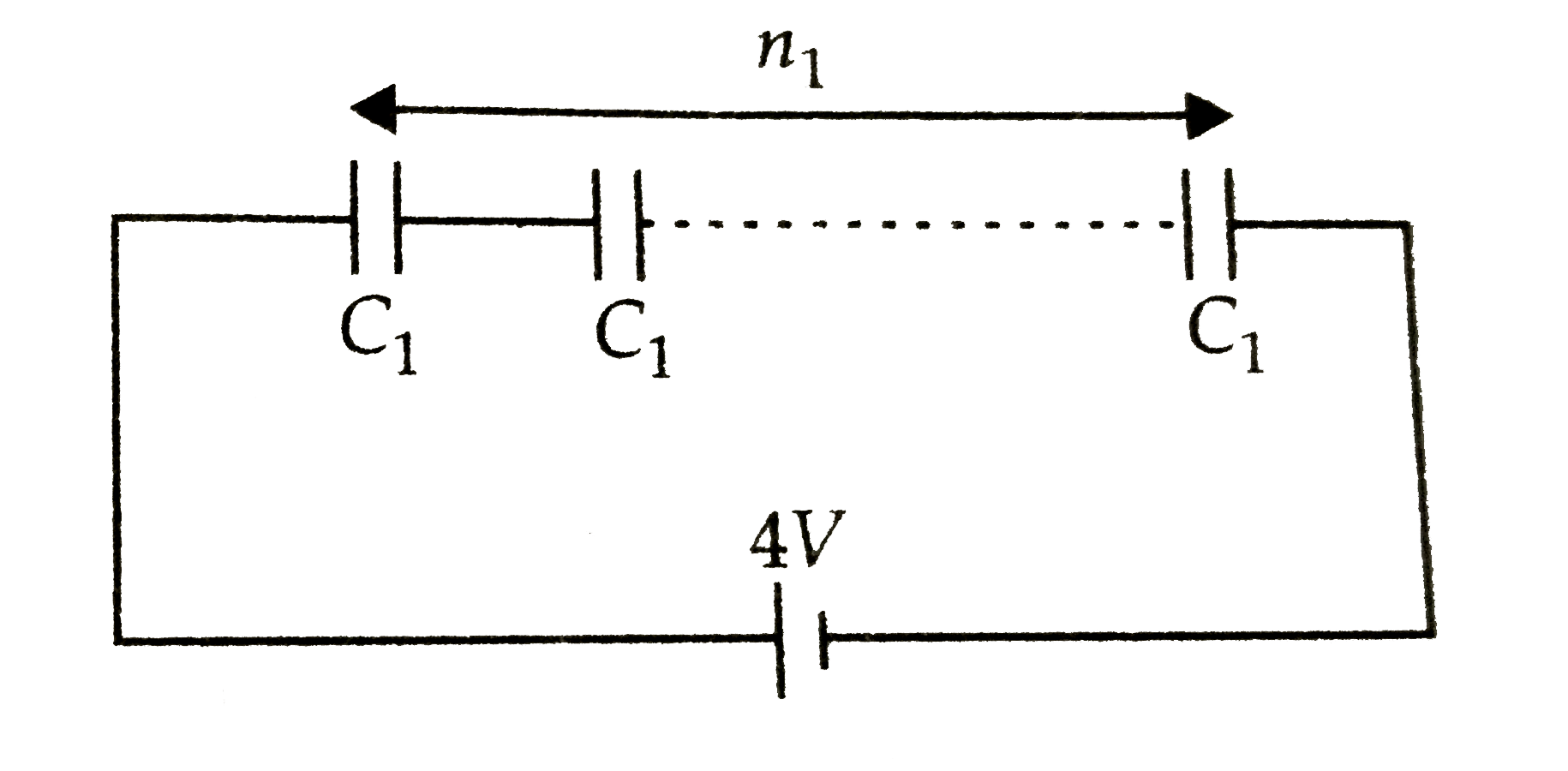
A series combination of n1 capacitors each of capacitance C1 are connecte to 4V source as shown in the figure .
Total capaciture of the series combination of the capacitors is given by .
Us=12Cs(4V)2=12(C1n1)(4V)2 (Using (i))......(ii))
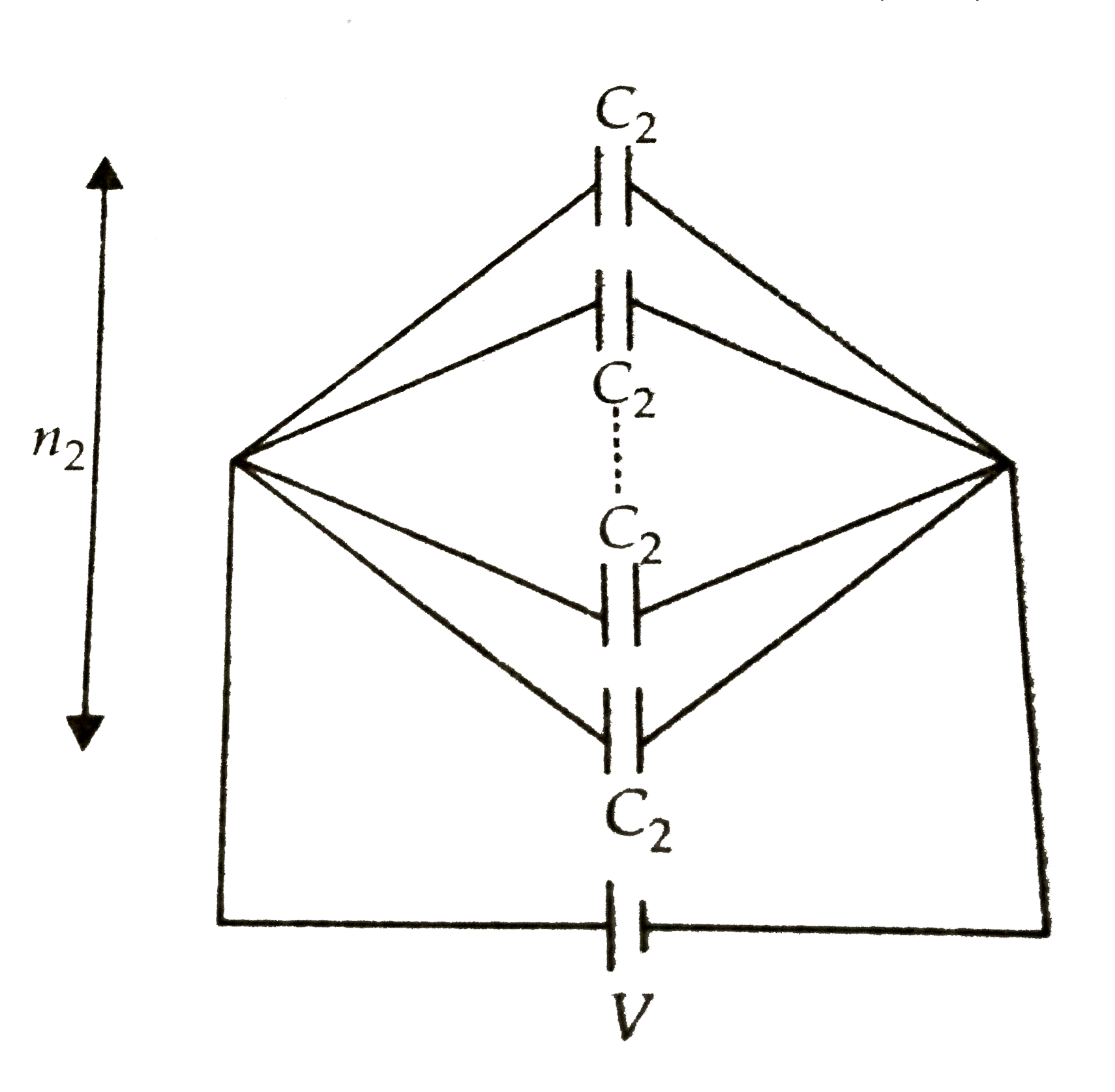
A parallel combination of n2 capacitors each of capacitance C2 are connected to V source to V source as shown in the figure.
Total energy stored in a parallel combintion of capacitors is Up=12CpV2=12(n2C2)(V)2 (Using (iii)).....(iv)
According to the given problem, Us=Up
12C1n1(4v)2=12(n2C2)(V)2
or C116n1=n2C2orC2=16C1n1n2
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTIPSCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Van De Graaff Generator
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTIPSCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Higher Order Thinking Skills
8 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTIPSCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Combination Of Capacitors
14 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTIPSCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTIPSCHAPTER - MAGNETISM AND MATTER EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A series combination of 5 capacitors, each of capacitance 1μF,is charged by a source of potential difference 2V. When another parallel combination of 10 capacitors each of capacitance C2 ,is charged by a source of potential difference V ,it has the same total energy stored in it as the first combination has.The value of C2 is
View SolutionFind the ratio of potential differences that must be applied across the parallel and series combination of two capacitors C1andC2 with their capacitance in the ratio 1 : 2 so that energy stored in the two cases becomes the same.
View Solution
Knowledge Check
A series combination of N1 capacitors (each of capacity C1) is charged to potential difference 3V. Another parallel combination of N2 capacitors (each of capacity C2) is charged to potential difference V. The total energy stored in both the combinations is same, The value of C1 in terms of C2 is
AC2N1N29BC2N21N229CC2N19N2DC2N29N1Parallel combination of two capacitors, each of value 10μF is charged by 200 volt d.c. Total energy of the capictor in joules will be :
A0.1B0.2C0.4D0.6A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
Find the ratio of potential difference that must be applied across the parallel and series combination of two capacitors C1andC2 with their capacitance in the ratio 1:3 so that energy stored in the two cases becomes the same.
View SolutionFind the ratio of the potential differences that must be applied across the parallel and series combination of two capacitors C1andC2 with their capacitances in the ratio 1 : 2 so that the energy stored in the two cases becomes the same.
View SolutionA capacitor is charged through a potential difference of 200V, when 0.1 C charge is stored in it. How much energy will it release, when it is discharge ?
View SolutionA capacitor when charged by a potential difference of 200 Volts, stores a charge of 0.1C. By discharging energy liberated by the capacitor is-
View Solutionn capacitors each of capacity C are joined in parallel. If they are connected to a source of V volts, then the energy stored in the capacitor is
View Solution
