A short magnet oscillation in vibration magnetometer with a frequency 10Hz. A downward current of 15A is established in a long vertical wire placed 20cm to the West of the magnet. The new frequency of the short magnet is (the horizontal of the component os earth's magnetic field is 12μ)
4Hz
2.5Hz
9Hz
15Hz
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Calculate the magnetic field due to the current-carrying wire.
The formula for the magnetic field B at a distance a from a long straight current-carrying wire is given by:
B=μ0I2πa
Where:
- μ0=4π×10−7T m/A (permeability of free space)
- I=15A (current)
- a=20cm=0.2m (distance from the wire)
Substituting the values into the formula:
B=(4π×10−7)×152π×0.2
Step 2: Simplify the expression.
The π in the numerator and denominator cancels out:
B=(4×10−7)×152×0.2
B=60×10−70.4
B=150×10−7T=1.5×10−5T=15μT
Step 3: Calculate the new magnetic field.
The total magnetic field B′ acting on the magnet is the sum of the horizontal component of the Earth's magnetic field Be and the magnetic field due to the wire B:
Given that Be=12μT:
B′=Be+B=12μT+15μT=27μT
Step 4: Relate the frequencies to the magnetic fields.
The frequency of oscillation f of a magnet in a magnetic field is proportional to the square root of the magnetic field:
f∝√B
Let f0=10Hz be the initial frequency and f′ be the new frequency. The relationship can be expressed as:
f′f0=√B′Be
Step 5: Substitute the values.
Substituting the known values:
f′10=√27μT12μT=√2712=√94=32
Step 6: Calculate the new frequency.
Now, we can find f′:
f′=10×32=15Hz
Final Answer:
The new frequency of the short magnet is 15Hz.
---
The formula for the magnetic field B at a distance a from a long straight current-carrying wire is given by:
- μ0=4π×10−7T m/A (permeability of free space)
- I=15A (current)
- a=20cm=0.2m (distance from the wire)
The π in the numerator and denominator cancels out:
B=60×10−70.4
B=150×10−7T=1.5×10−5T=15μT
The total magnetic field B′ acting on the magnet is the sum of the horizontal component of the Earth's magnetic field Be and the magnetic field due to the wire B:
The frequency of oscillation f of a magnet in a magnetic field is proportional to the square root of the magnetic field:
Substituting the known values:
Now, we can find f′:
The new frequency of the short magnet is 15Hz.
Similar Questions
A short bar magnet oscillates in VMM with a frequency of 10Hz. If a downward current of 15A is established in a long thin vertical wire placed 20 cm west of the magnet, its frequency was found to be 5Hz. If a TG containing 500 turns with radius of each turn 4π cm is used at that place & a current of 10mA is allowed to pass through it. Find the deflection of magnetic needle in the TG
View SolutionA current canying straight wire is placed along east-west and current is passed through it eastward . The direction of the force act on it due to horizontal component of earth's magnetic field is
View SolutionA short magnet oscillates in a vibration magnetometer with a time period of 0.10 s where the horizontal component of earth's magnetic field is 24μT . An upward current of 18 A is established in the vertical wire placed 20 cm east of the magnet . Find the new time period.
View SolutionCalculate earth's magnetic field at a place where angle of dip δ is 60∘ and horizontal component of earth's magnetic field is 0.3 G
View SolutionAt a place, the horizontal component of earth's magnetic field is B and angle of dip is 60∘. What is the value of horizontal component of earth's magnetic field at equator?
View SolutionAt a place, the horizontal component of earth's magnetic field is V and angle of dip is 60∘. What is te value of horizontal component of earth's magnetic field at equator ?
View SolutionLet V and H be the vertical and horizontal components of earth's magnetic field at any point on earth. Near the north pole
View SolutionFigure shows a short magnet executing small oscillations in an oscillation magnetometer in earth's magnetic field having horizontal component 24μT. The time period of oscillation is 0.10s. An upward electric current of 18A is established in the vertical wire placed 20cm east of the magnet by closing the switch S. Find the new time period
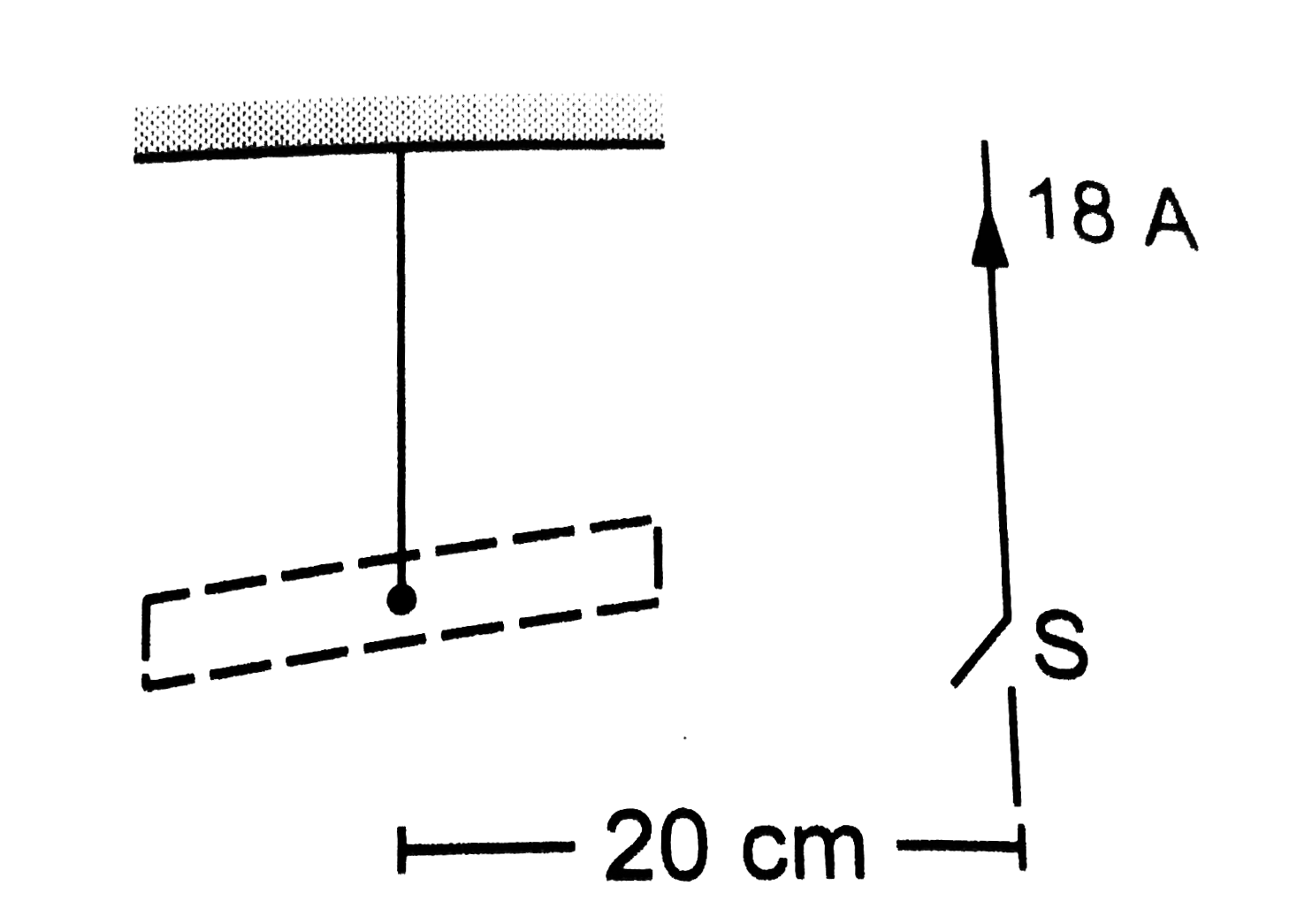
View SolutionA short bar magnet placed in a horizontal plane has its axis aligned along the magnetic north south direction. Null points are found on the axis of the magnet at 14cm from the centre of the magnet. The earth's magnetic field at the plane is 0⋅36G and the angle of dip is zero. What is the total magnetic field on the normal bisector of the magnet at the same distance as the null points (i.e. 14 cm) from the centre of the magnet? (At null points, field due to a magnet is equal and apposite to the horizontal component of earth's magnetic field).
View SolutionA magnetic dipole of magnetic moment 1.44Am2 is placed horizontally with the north pole pointing towards north. Find the positon of the neutral point if the horizontal component of the earth's magnetic field is 18μT.
View Solution
