(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
(E2−E1).n=σε0
where ˆn is a unit vector normal to the surface at a point and σ is the surface charge density at that point. (The direction of ˆn is from side 1 to side 2.) Hence, show that just outside a conductor, the electric field is σˆn/ε0.
(b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another. [Hint: For (a), use Gauss’s law. For, (b) use the fact that work done by electrostatic field on a closed loop is zero.]Solution in Gujrati
Electric field near the surface of a charged plane plate,
E=σ2∈0
If electric field is considered to be vector then the unit vector ˆn is one side and - ˆn is other side of plane.
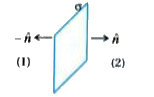
Electric field from side (1) to side (2),
→E2=σ2∈0.ˆn
Electric field from s.ide (2) to side (1),
→E1=−σ2∈0.ˆn
Electric field to side (1)
(→E2−→E1)=[σ2∈0−(−σ2∈0)]ˆn
=2σ2∈0ˆn
=σ∈0ˆn
where σ is the surface charge density and unit vector ˆn is from side (1) to side (2),
Since E1 and E2 are opposite to each othe so electric field has discontinuity on plat and the electric field disappear inside the conductor hence
→E1=0
So, electric field outside the conductor
→E=→E2=σ∈0ˆn
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B ( Numerical From DARPAN. Based on Textbook )
19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B (questions)
2 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B Numericals
16 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
- MAGNETISM AND MATTERBOOK - KUMAR PRAKASHANCHAPTER - MAGNETISM AND MATTEREXERCISE - SECTION D Multiple Choice Questions (MCQs) (MCQs asked in Competitive Exams) MCQs asked in Board Exam and GUJCET
7 Videos
Similar Questions
An electric field is represented by →E=Axˆi where A = 10Vm2 . Find the potential of the origin with respect to the point (10,20) m.
View SolutionA slab of material of dielectric constant K has the same area as the plates of a parallel plate capacitor but has a thickless (12)d. Where d is the separation of the plates . How is the capacitance changed when the slab is inserted between the plates
View SolutionCalculate the potential at a point P due to a charge of 4×10−7 C located 9 cm away.
View SolutionDetermine the current in each branch of the given network.

View SolutionAt a place on earth the vertical component of earth's magnetic field is √3 times its horizontal component. The angle of dip at this place is …...
View SolutionShow that the normal component of electrostatic field has a discontinuly form one side of a charged. Surface to another given by (−→E2−−→E1).ˆn=σ∈0
where ˆn is a unit vector normal to the surface at a point and σ at a point and σ is the surface charge density at that point. (The direction of ˆn is from side 1 to side 2). Hence show that justy outside a conductor, the electric field σˆn/∈0.
(b) Show that the tangential componet of electrostatic field is contionous from one side fo a charged surface to another.
View Solution(a) दर्शाइए कि आवेशित पृष्ठ के एक पार्श्व पर स्थिरवैद्युत क्षेत्र के अभिलम्ब घटक में असांतत्य होता है, जिसे
(E2−E1).ˆn=Qe0
द्वारा व्यक्त किया जाता है । जहाँ ˆn एक बिंदु पर पृष्ठ के अभिलम्ब एकांक सदिश है तथा Q उस बिंदु पर पृष्ठ आवेश घनत्व है (ˆn की दिशा पार्श्व 1 से पार्श्व 2 की ओर है ।)। अतः दर्शाइए चालक के ठीक बाहर वैद्युत क्षेत्र Qˆn/e0 है ।
(b) दर्शाइए कि आवेशित पृष्ठ के एक पार्श्व पर स्थिरवैद्युत क्षेत्र का स्पशीर्य घटक संतत है ।
View SolutionShow that the electric field at the surface of a charged conductor is given by vecE = (sigma)/(epsi_(0)) hatn , where sigma is the surface charge density and hatn is a unit vector normal to the surface in the outward direction .
View Solutionदर्शाइए की आवेशित पृष्ठ के एक पाशर्व पर स्थिरवैद्युत क्षेत्र के अभिलंब घटक में असांतत्य होता है , जिस
(E2−E1).ˆn=σ∈0
द्वारा व्यक्त किया जाता है जहाँ ˆn एक बिन्दु पर पृष्ठ के अभिलंब एकांक सदिश है तथा σ उस बिंदु पर पृष्ठ आवेश धनत्व है (ˆn की दिशा पाशर्व1 से पाशर्व 2 की ओर है ) | अतः
दर्शाइए की चालक के ठीक बहार विद्युत क्षेत्र σˆn/∈0 है |
View SolutionShow that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by (E2−E1).∧n=σε0
Where ∧n is a nuit vector normal to the surface at a point and σ is the surface charge density at that point . (The direction of ∧n is from side 1 to side 2.) Hence show that just out side a conductor , the electric field is σ∧n/ε0.
(b) Show that the tangential component of electrostatic field is continuous from one side of a charge surface of another. use the fact that work done by electrostatic field on a closed loop is zero. )
View Solution(a ) सिद्ध करे कि किसी आवेशित सतह ( charged surface) के एक ओर से दूसरी ओर जाने के क्रम में विद्युत - क्षेत्र →E के लंबवत घटक (normal component) में असांतत्य ( discontinuity ) होता है, जिसे (→E2−→E1)⋅ˆn=σ∈0 द्वारा व्यक्त किया जाता है | सतह 1 से सतह 2 की ओर उस बिंदु पर अभिलम्ब एकांक सदिश =ˆn तथा सतह के उस बिंदु पर आवेश का पृष्ठ - घनत्व = σ है | अतः, सिद्ध करे कि आवेशित चालक के ठीक बाहर विद्युत - क्षेत्र σˆn∈0 है |
(b) प्रमाणित करे कि आवेशित सतह के एक ओर से दूसरी ओर जाने के क्रम में स्थिर विद्युत - क्षेत्र का स्पर्शीय घटक ( tangential component) संतत ( continuous ) रहता है |
View SolutionWhat is the electric field in between the plates of the capacitor, if σ is the surface charge density?
View Solution(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
(E2−E1).n=σε0
where ˆn is a unit vector normal to the surface at a point and σ is the surface charge density at that point. (The direction of ˆn is from side 1 to side 2.) Hence, show that just outside a conductor, the electric field is σˆn/ε0.
(b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another. [Hint: For (a), use Gauss’s law. For, (b) use the fact that work done by electrostatic field on a closed loop is zero.]
View Solution(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
(E2−E1).n=σε0
where ˆn is a unit vector normal to the surface at a point and σ is the surface charge density at that point. (The direction of ˆn is from side 1 to side 2.) Hence, show that just outside a conductor, the electric field is σˆn/ε0.
(b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another. [Hint: For (a), use Gauss’s law. For, (b) use the fact that work done by electrostatic field on a closed loop is zero.]
View SolutionA hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hole is (σ2∈0)ˆn , where ˆn is the unit vector in the outward normal direction, and σ is the surface charge density near the hole,
View SolutionShow that the electric field at the surface of a charged conductor is given by →E=σ60ˆn , where σ is the surface charge density and ˆn is a unit vector normal to the surface in the outward direction.
View Solution
