(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
(E2−E1).n=σε0
where ˆn is a unit vector normal to the surface at a point and σ is the surface charge density at that point. (The direction of ˆn is from side 1 to side 2.) Hence, show that just outside a conductor, the electric field is σˆn/ε0.
(b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another. [Hint: For (a), use Gauss’s law. For, (b) use the fact that work done by electrostatic field on a closed loop is zero.]Solution in Gujrati
Suppose, xy is a charged surface of dielectric and electric field →E1 and →E2 are on its both side.
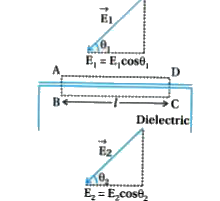
Let loop ABCD. Its length is l and width is negligible.
Line integration of closed path of ABCD ,
∫→E.d→l=→E1.→l−→E2.→l=0
=E1lcosθ1−E2lcosθ2=0
∴(E1cosθ1−E2cosθ2)l=0
∴(E1−E2)l=0
where E1 and E2 aretangenticalcomponent
∴E1=E2
∴ Hence, the tangential component of electrostatic field is continuous from one side of a charged surface to the other.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B ( Numerical From DARPAN. Based on Textbook )
19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B (questions)
2 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section B Numericals
16 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
- MAGNETISM AND MATTERBOOK - KUMAR PRAKASHANCHAPTER - MAGNETISM AND MATTEREXERCISE - SECTION D Multiple Choice Questions (MCQs) (MCQs asked in Competitive Exams) MCQs asked in Board Exam and GUJCET
7 Videos
Similar Questions
An electric field is represented by →E=Axˆi where A = 10Vm2 . Find the potential of the origin with respect to the point (10,20) m.
View SolutionA slab of material of dielectric constant K has the same area as the plates of a parallel plate capacitor but has a thickless (12)d. Where d is the separation of the plates . How is the capacitance changed when the slab is inserted between the plates
View SolutionCalculate the potential at a point P due to a charge of 4×10−7 C located 9 cm away.
View SolutionDetermine the current in each branch of the given network.

View SolutionAt a place on earth the vertical component of earth's magnetic field is √3 times its horizontal component. The angle of dip at this place is …...
View SolutionShow that the normal component of electrostatic field has a discontinuly form one side of a charged. Surface to another given by (−→E2−−→E1).ˆn=σ∈0
where ˆn is a unit vector normal to the surface at a point and σ at a point and σ is the surface charge density at that point. (The direction of ˆn is from side 1 to side 2). Hence show that justy outside a conductor, the electric field σˆn/∈0.
(b) Show that the tangential componet of electrostatic field is contionous from one side fo a charged surface to another.
View Solution(a) दर्शाइए कि आवेशित पृष्ठ के एक पार्श्व पर स्थिरवैद्युत क्षेत्र के अभिलम्ब घटक में असांतत्य होता है, जिसे
(E2−E1).ˆn=Qe0
द्वारा व्यक्त किया जाता है । जहाँ ˆn एक बिंदु पर पृष्ठ के अभिलम्ब एकांक सदिश है तथा Q उस बिंदु पर पृष्ठ आवेश घनत्व है (ˆn की दिशा पार्श्व 1 से पार्श्व 2 की ओर है ।)। अतः दर्शाइए चालक के ठीक बाहर वैद्युत क्षेत्र Qˆn/e0 है ।
(b) दर्शाइए कि आवेशित पृष्ठ के एक पार्श्व पर स्थिरवैद्युत क्षेत्र का स्पशीर्य घटक संतत है ।
View SolutionShow that the electric field at the surface of a charged conductor is given by vecE = (sigma)/(epsi_(0)) hatn , where sigma is the surface charge density and hatn is a unit vector normal to the surface in the outward direction .
View Solutionदर्शाइए की आवेशित पृष्ठ के एक पाशर्व पर स्थिरवैद्युत क्षेत्र के अभिलंब घटक में असांतत्य होता है , जिस
(E2−E1).ˆn=σ∈0
द्वारा व्यक्त किया जाता है जहाँ ˆn एक बिन्दु पर पृष्ठ के अभिलंब एकांक सदिश है तथा σ उस बिंदु पर पृष्ठ आवेश धनत्व है (ˆn की दिशा पाशर्व1 से पाशर्व 2 की ओर है ) | अतः
दर्शाइए की चालक के ठीक बहार विद्युत क्षेत्र σˆn/∈0 है |
View SolutionShow that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by (E2−E1).∧n=σε0
Where ∧n is a nuit vector normal to the surface at a point and σ is the surface charge density at that point . (The direction of ∧n is from side 1 to side 2.) Hence show that just out side a conductor , the electric field is σ∧n/ε0.
(b) Show that the tangential component of electrostatic field is continuous from one side of a charge surface of another. use the fact that work done by electrostatic field on a closed loop is zero. )
View Solution(a ) सिद्ध करे कि किसी आवेशित सतह ( charged surface) के एक ओर से दूसरी ओर जाने के क्रम में विद्युत - क्षेत्र →E के लंबवत घटक (normal component) में असांतत्य ( discontinuity ) होता है, जिसे (→E2−→E1)⋅ˆn=σ∈0 द्वारा व्यक्त किया जाता है | सतह 1 से सतह 2 की ओर उस बिंदु पर अभिलम्ब एकांक सदिश =ˆn तथा सतह के उस बिंदु पर आवेश का पृष्ठ - घनत्व = σ है | अतः, सिद्ध करे कि आवेशित चालक के ठीक बाहर विद्युत - क्षेत्र σˆn∈0 है |
(b) प्रमाणित करे कि आवेशित सतह के एक ओर से दूसरी ओर जाने के क्रम में स्थिर विद्युत - क्षेत्र का स्पर्शीय घटक ( tangential component) संतत ( continuous ) रहता है |
View SolutionWhat is the electric field in between the plates of the capacitor, if σ is the surface charge density?
View Solution(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
(E2−E1).n=σε0
where ˆn is a unit vector normal to the surface at a point and σ is the surface charge density at that point. (The direction of ˆn is from side 1 to side 2.) Hence, show that just outside a conductor, the electric field is σˆn/ε0.
(b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another. [Hint: For (a), use Gauss’s law. For, (b) use the fact that work done by electrostatic field on a closed loop is zero.]
View Solution(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
(E2−E1).n=σε0
where ˆn is a unit vector normal to the surface at a point and σ is the surface charge density at that point. (The direction of ˆn is from side 1 to side 2.) Hence, show that just outside a conductor, the electric field is σˆn/ε0.
(b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another. [Hint: For (a), use Gauss’s law. For, (b) use the fact that work done by electrostatic field on a closed loop is zero.]
View SolutionA hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hole is (σ2∈0)ˆn , where ˆn is the unit vector in the outward normal direction, and σ is the surface charge density near the hole,
View SolutionShow that the electric field at the surface of a charged conductor is given by →E=σ60ˆn , where σ is the surface charge density and ˆn is a unit vector normal to the surface in the outward direction.
View Solution
