A silica glass rod has a diameter of1cmand is 10 cmlong. The ultimate strength of glass is 50x106Nm−2. Estimate the largest mass that can be hung from it without breaking it. Take g=10Nkg−1.
To solve the problem of estimating the largest mass that can be hung from a silica glass rod without breaking it, we will follow these steps:
Step 1: Understand the given data
- Diameter of the rod, d=1cm=0.01m
- Length of the rod, L=10cm=0.1m
- Ultimate strength (breaking stress) of glass, σmax=50×106N/m2
- Acceleration due to gravity, g=10N/kg
Step 2: Calculate the cross-sectional area of the rod
The cross-sectional area A of the rod can be calculated using the formula for the area of a circle:
A=π(d2)2=π(0.012)2=π(0.005)2=π×0.000025m2
A≈7.85×10−5m2
Step 3: Relate stress, force, and area
The stress σ is defined as the force F applied per unit area A:
σ=FA
The force F can also be expressed in terms of mass m and gravitational acceleration g:
F=m⋅g
Step 4: Set up the equation for maximum mass
At maximum stress, we have:
σmax=mmax⋅gA
Rearranging this gives:
mmax=σmax⋅Ag
Step 5: Substitute the values into the equation
Substituting the known values:
mmax=50×106N/m2⋅7.85×10−5m210N/kg
Calculating this gives:
mmax=3925N10N/kg=392.5kg
Conclusion
The largest mass that can be hung from the silica glass rod without breaking it is approximately 392.5 kg.
---
- Diameter of the rod, d=1cm=0.01m
- Length of the rod, L=10cm=0.1m
- Ultimate strength (breaking stress) of glass, σmax=50×106N/m2
- Acceleration due to gravity, g=10N/kg
The cross-sectional area A of the rod can be calculated using the formula for the area of a circle:
A=π(d2)2=π(0.012)2=π(0.005)2=π×0.000025m2
A≈7.85×10−5m2
The stress σ is defined as the force F applied per unit area A:
σ=FA
The force F can also be expressed in terms of mass m and gravitational acceleration g:
F=m⋅g
At maximum stress, we have:
σmax=mmax⋅gA
Rearranging this gives:
mmax=σmax⋅Ag
Substituting the known values:
mmax=50×106N/m2⋅7.85×10−5m210N/kg
Calculating this gives:
mmax=3925N10N/kg=392.5kg
The largest mass that can be hung from the silica glass rod without breaking it is approximately 392.5 kg.
Topper's Solved these Questions
- Mechanical Properties of SolidsBOOK - SL ARORACHAPTER - Mechanical Properties of SolidsEXERCISE - Example
113 Videos
- Mechanical Properties of fluidsBOOK - SL ARORACHAPTER - Mechanical Properties of fluidsEXERCISE - Exercise
459 Videos
- MECHANICSBOOK - SL ARORACHAPTER - MECHANICSEXERCISE - Exercise
341 Videos
Similar Questions
The mass of an object whose weight is 50 N is x kg. Find x. (Take g=10ms−2)
View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2
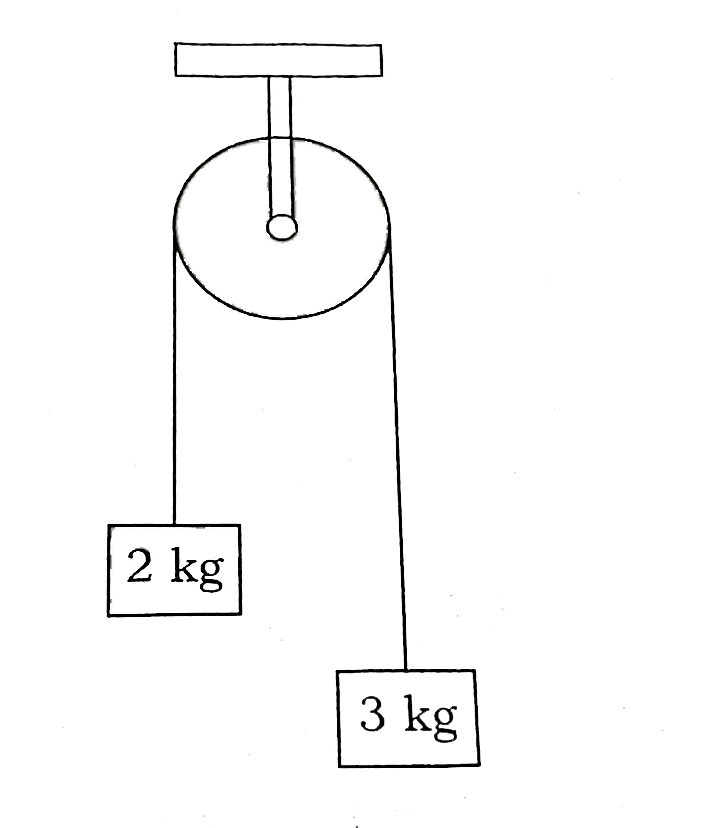
View Solution
Knowledge Check
In the above problem if the the yield strength of steel is 2.5×108N/m2, then the maximum mass that can be hung at the lower end of the wire is
A785kgB78.75kgC78.25kgD78.50kgThe breaking tension of a string is 10 N. A particle of mass 0.1 kg tied to it is rotated along a horizontal circle of radius 0.5 meter. The maximum speed with which the particle can be rotated without breaking the string is
A√5m/secB√(50)m/secC√(500)m/secD√(1000)m/secA nylon rope 2cm in diameter has a breaking strength of 1.5×105N. The breaking strength of a similar rope 1cm in diameter is
A0.375×105NB2×105NC6×105ND9×104N
Two blocks of masses 1 kg and 2kg are connect by a metal wire going over a smooth pulley as shown in figure. The breaking stress of the metal is 2×109m−2. What should be the minmum radius of the wire used if it is not to break? Take g=10ms−2
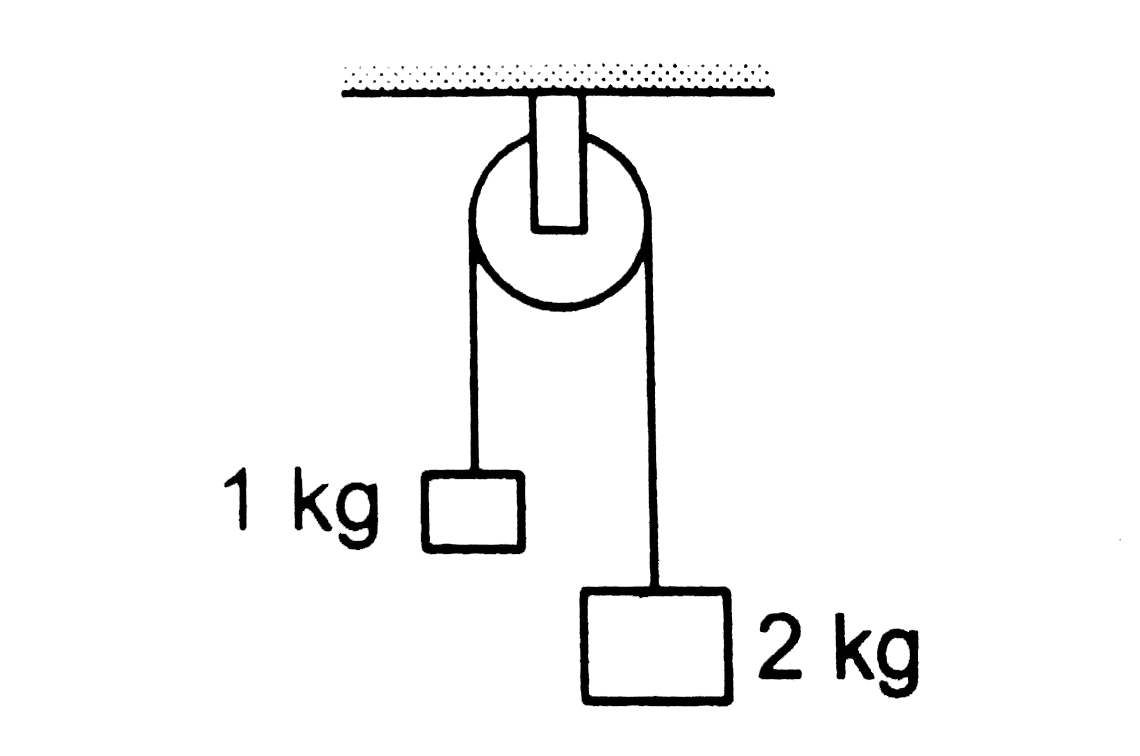
View SolutionThe breaking stress for a metal is 7.8×109Nm−2. Calculate the maximum length of the wire of this metal which may be suspended breaking. The density of the metal =7.8×103kgm−3. Take g =10Nkg−1
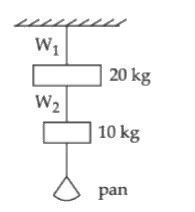
View SolutionWires W1 and W2 are made of same material having the breaking stress of 1.25×109N/m2.W1andW2 have cross-sectional area of 8×10−7m2and4×10−7m2, respectively. Masses of 20 kg and 10 kg hang from them as shown in the figure. The maximum mass that can be placed in the pan without breaking the wires is kg. (Use g=10m/s2)
View SolutionThe breaking stress for a metal is 9×1010Nm−2 The density of the metal is 9000kgm−3 . If g=10Nkg−1 , the maximum length of the wire made of this metal which may be suspended without breaking is 10k m . Find the value of k.
View SolutionTwo blocks of masses 3 kg and 5 kg are connected by a metal wire going over a smooth pulley. The breaking stress of the metal is 24π×102Nm−2 . What is the minimum radius of the wire ?
(take g=10ms−2)
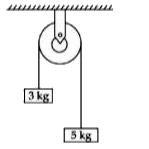
View Solution
