Two blocks of masses 1 kg and 2kg are connect by a metal wire going over a smooth pulley as shown in figure. The breaking stress of the metal is 2×109m−2. What should be the minmum radius of the wire used if it is not to break? Take g=10ms−2
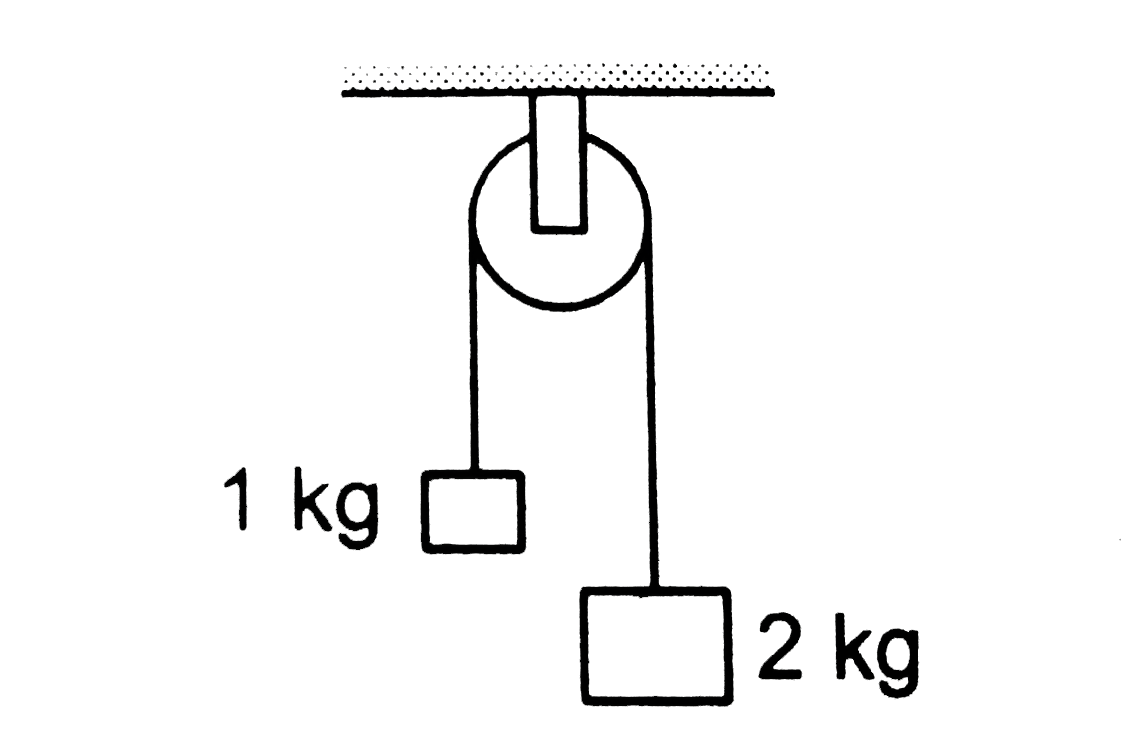
The stress in the wire =TensionAreaofcrosssection
To avoid breaking, this stress should not exceed the breaking stress.
Let the tension in the wire be T. The equations of motion of the two blocks are
T−10N=(1kg)a
and20N−T=(2kg)a
ElimiN/Ating a from these equations
T=(403)N
Thestress=(403)Nπr2
If the minimum radius needed to avoid breaking is r, 2×109Nm2=(403)Nπr2
solv∈gthis<br>r=4.6xx10^-5m.
Topper's Solved these Questions
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Short Answer
18 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective 1
29 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- SOUND WAVESBOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - Exercises
89 Videos
Similar Questions
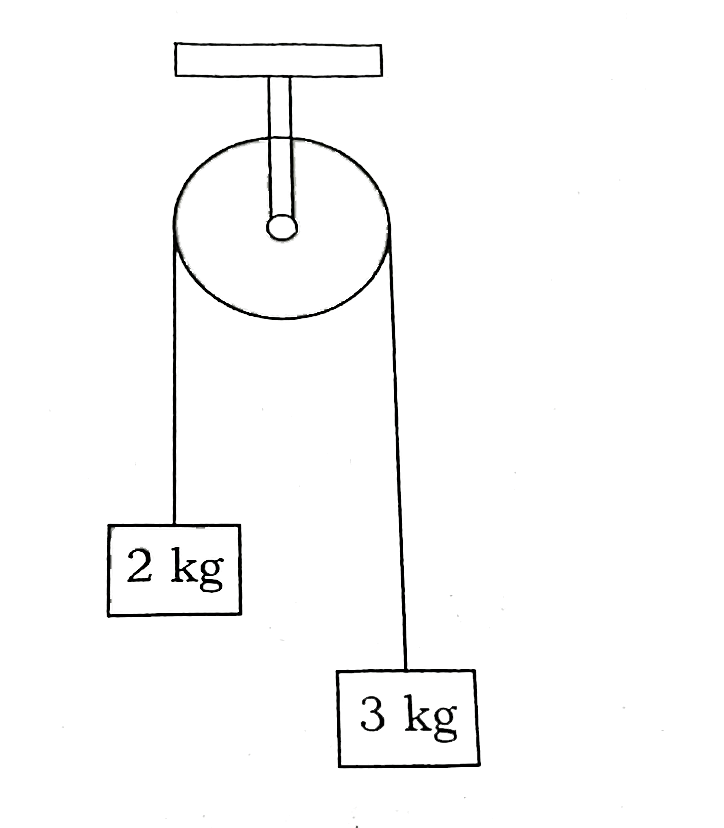
Two blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2
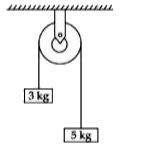
View SolutionTwo blocks of masses 3 kg and 5 kg are connected by a metal wire going over a smooth pulley. The breaking stress of the metal is 24π×102Nm−2 . What is the minimum radius of the wire ?
(take g=10ms−2)
View Solution
Knowledge Check
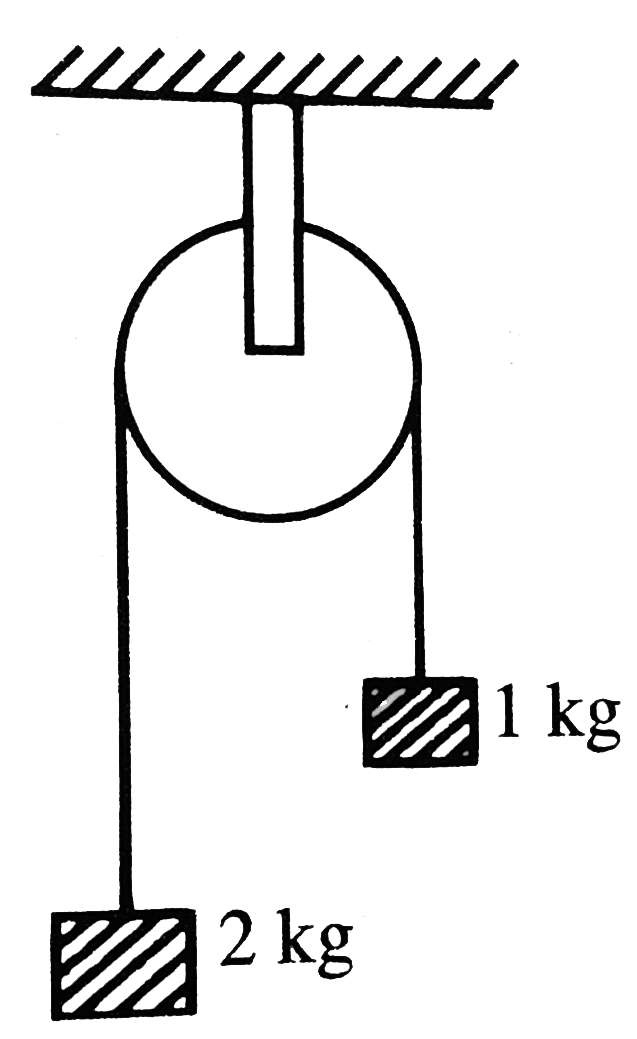
Two blocks of masses 1kg and 2kg are connected by a metal wire goijng over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−12, then what should be the minimum radlus of the wire used if it is not to break?
 A0.5mmB1mmC1.5mmD2mm
A0.5mmB1mmC1.5mmD2mmTwo blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2×109N m−2. If g=10ms−2, then what is the minimum radius of the wire which will not break
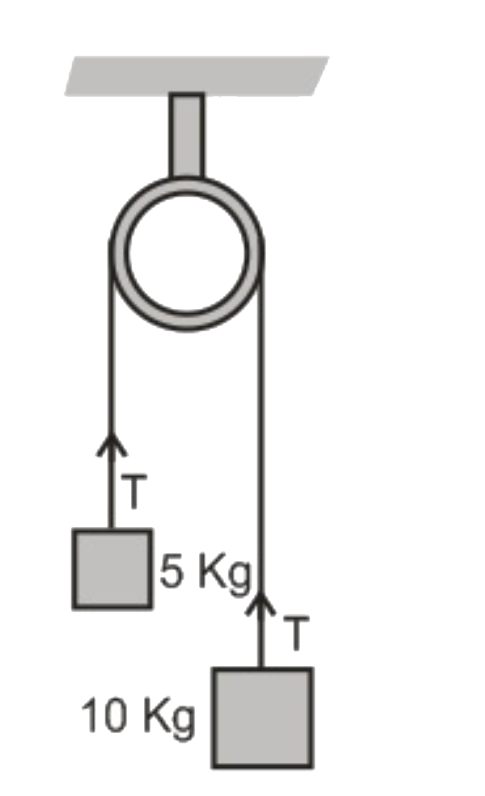 A0.1 mmB0.2 mmC0.05 mmD0.25 mm
A0.1 mmB0.2 mmC0.05 mmD0.25 mmTwo blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is
 A50N up the planeB50N down the planeC100N up the planeD100N down the plane
A50N up the planeB50N down the planeC100N up the planeD100N down the plane
Two masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
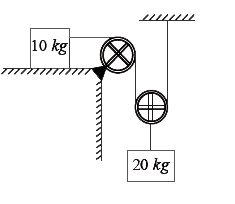
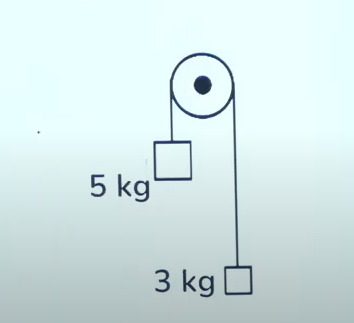
View SolutionA wire is supporting two masses on a pulley as shown. If breaking stress of wire is (2400π)Nm−2. Find minimum radius of wire, so that it does not break.
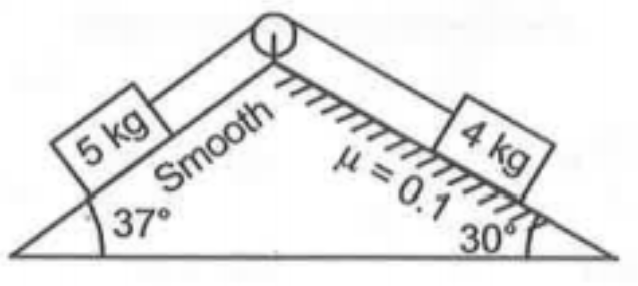
View SolutionTwo blocks of masses 5 kg and 4 kg are connected with ideal string which is passing over an ideal pulley as shown in figure. If the system is released from rest then the magnitude of acceleration of the blocks will be (Take g=10ms−2and√3=1.7)
View SolutionThree blocks of masses m1=4kg,m2=2kg,m3=4kg are connected with ideal strings passing over a smooth, massless pulley as shown in figure. The acceleration of blocks will be (g=10m/s2)
View SolutionTwo unequal masses of 1kg and 2kg are connected by an inextensible light string passing over a smooth pulley as shown in figure. A force F=20N is applied on 1kg block find the acceleration of either block (g=10m/s2).

View Solution
