A simple pendulum has a bob of mass m which carries a charge q on it. Length of the pendulum is L. There is a uniform electric field E in the region. Calculate the time period of small oscillations for the pendulum about its equilibrium position in following cases:
(i). E is vertically down having magnitude
(ii). E is vertically up having magnitude
(iii). E is horizontal having magnitude
(iv). E has magnitude of E=q and is directed upward making an angle with the horizontal
The correct Answer is:(i)
(ii).
(iii).
(iv).
Step by step video, text & image solution for A simple pendulum has a bob of mass m which carries a charge q on it. Length of the pendulum is L. There is a uniform electric field E in the region. Calculate the time period of small oscillations for the pendulum about its equilibrium position in following cases: (i). E is vertically down having magnitude E=(mg)/(q) (ii). E is vertically up having magnitude E=(2mg)/(q) (iii). E is horizontal having magnitude E=(mg)/(q) (iv). E has magnitude of E=q and is directed upward making an angle 45^(@) with the horizontal by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 2
77 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 3
9 Videos
Similar Questions
A simple pendulum of length l and having a bob of mass M is suspended ina car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium, what will be its time period ?
View SolutionA simple pendulum has time period T. Charges are now fixed at the point of suspension of the pendulum and on the bob. If the pendulum continues to oscillate, its time period will now be
View Solution
Knowledge Check
A simple pendulum has a length l & mass of bob m. The bob is given a charge q coulomb. The pendulum is suspended in a uniform horizontal electric field of strength E as shown in figure, then calculate the time period of oscillation when bob is slightly displaced from its mean position.
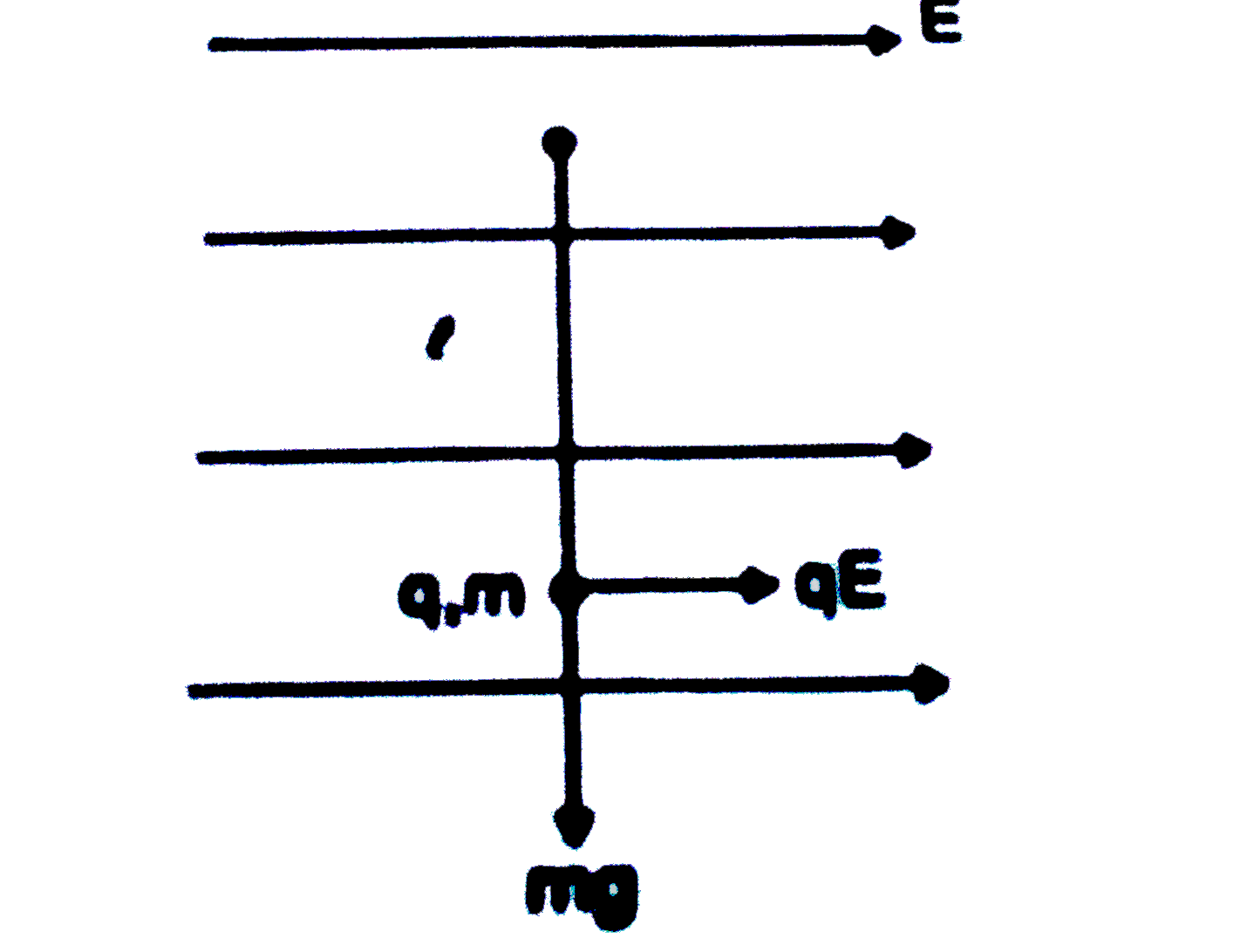 A2π√lgB2π ⎷⎧⎨⎩lg+qEm⎫⎬⎭C2π ⎷⎧⎨⎩lg−qEm⎫⎬⎭D2π ⎷l√g2+(qEm)2
A2π√lgB2π ⎷⎧⎨⎩lg+qEm⎫⎬⎭C2π ⎷⎧⎨⎩lg−qEm⎫⎬⎭D2π ⎷l√g2+(qEm)2If a simple pendulum has charge q and is oscillating in a uniform electric field E in the direction of acceleration due to gravity, then its frequency of oscillations
AincreasesBdecreasesCfirst increases and later on it remains constantDindependent of the effect of electric fieldA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
AmgsinθBmgCqEsinθDqEcosθ
An electron having charge 'e' and mass 'm' is moving a uniform electric field E. Its acceleration will be
View SolutionA simple pendulum of length 'l' carries a bob of mass 'm'. If the breaking strength of the string is 3mg, the maximum angular amplitude from the vertical can be
View SolutionA positively charged pendulum is oscillating in a uniform electric field as shown in Figure. Its time period of SHM as compared to that when it was uncharged. (mg>qE)

View SolutionA mass m carrying a charge q si suspended form a string and placed in a uniform horizontal electric field of intensity E.The angel made by the string with the vertical in the equilibrium position is
View SolutionAn oil drop of mass m and charge +q is balanced in vaccum by a uniform electric field of intensity E. the direction of this field should be
View Solution
