A uniform semicircular ring of radius R is in yz plane with its centre at the origin. The half ring carries a uniform linear charge density of .
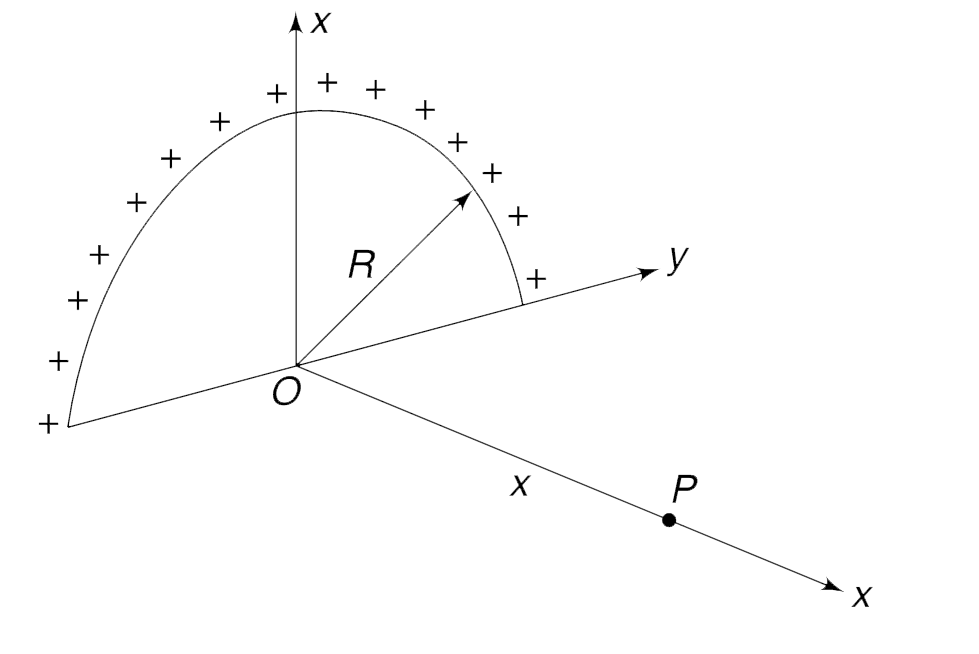
(a) Find the x, y and z component of Electric field at a point P(x, 0, 0) on the axis of the ring. (b) Prove that the field at P is directed along a line joining the centre of mass of the half ring to the point P.
The correct Answer is:(a)
(b).
(c).
Topper's Solved these Questions
Similar Questions
A circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
View SolutionA circular ring lying in the x-y plane with its centre at the origin carries a uniformly distributed positive charge. The variation of the electric field E at the point (0,0,z) is correctly represented by the graph is
View Solution
Knowledge Check
A ring with a uniform charge Q and radius R, is placed in the yz plane with its centre at the origin
Athe field at the origin is zeroBThe potential at the origin is kQRCthe potential at the origin is kQx2Dthe filled at the point (x,0,0) is kQR2+x2A circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
Aλ3√3ε0RB2λ3√3ε0R2C23√3λε0RDnone the theseA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
Aλ4εoln0Bλ4π2ε0rCλ4πε0rDλ4πε0r2
A half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View SolutionA sermicircular ring of radius R carries a uniform linear charge of λ. P is a point in the plane of the ring at a distance R from centre O. OP is perpendicular to AB. Find electric field intensity at point P.
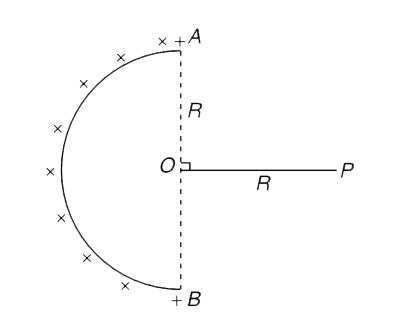
View SolutionA quarter ring of radius R is having uniform charge density λ. Find the electric field and potential at the centre of the ring.
View SolutionA thin circular ring of radius r is charged uniformly so that its linear charge density becomes λ . Derive an expression for the electric field at a point P at a distance x from it along the axis of the ring. Hence, prove that at large distances (r >> r), the ring behaves as a point charge.
View SolutionA ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
View Solution
