A simple pendulum has a bob which is a hollow sphere full of sand and oscillated with certain period. If all that sand is drained out through a hole at its bottom, then its period
(a) increases
(b) decreases
( c) remains same
(d) is zero.
The correct Answer is:C
To solve the question regarding the effect of draining sand from a hollow sphere bob of a simple pendulum on its period, we can follow these steps:
Step 1: Understand the Formula for the Period of a Simple Pendulum
The period T of a simple pendulum is given by the formula:
T=2π√Lg
where:
- T is the period,
- L is the length of the pendulum,
- g is the acceleration due to gravity.
Step 2: Analyze the Initial Condition
Initially, the pendulum bob is a hollow sphere filled with sand. The effective mass of the bob is greater due to the sand, but the length L remains constant.
Step 3: Consider the Effect of Draining the Sand
When the sand is drained out:
- The mass of the bob decreases, but the length L of the pendulum does not change immediately.
- As the sand drains, the distribution of mass changes, which can affect the moment of inertia and the effective length of the pendulum.
Step 4: Determine the Immediate Effect on the Period
Initially, as the sand drains, the period of the pendulum may increase due to the change in effective length and mass distribution. However, the length L remains constant, and thus the immediate effect is that the period may increase.
Step 5: Final Condition After All Sand is Drained
Once all the sand is drained out, the bob is now a hollow sphere with no sand inside. The effective mass distribution stabilizes, and the period of the pendulum returns to its original value, which was determined by the length L.
Conclusion
Thus, after all the sand is drained, the period of the pendulum remains the same as it was initially. Therefore, the correct answer is:
(c) remains same.
---
The period T of a simple pendulum is given by the formula:
T=2π√Lg
where:
- T is the period,
- L is the length of the pendulum,
- g is the acceleration due to gravity.
Initially, the pendulum bob is a hollow sphere filled with sand. The effective mass of the bob is greater due to the sand, but the length L remains constant.
When the sand is drained out:
- The mass of the bob decreases, but the length L of the pendulum does not change immediately.
- As the sand drains, the distribution of mass changes, which can affect the moment of inertia and the effective length of the pendulum.
Initially, as the sand drains, the period of the pendulum may increase due to the change in effective length and mass distribution. However, the length L remains constant, and thus the immediate effect is that the period may increase.
Once all the sand is drained out, the bob is now a hollow sphere with no sand inside. The effective mass distribution stabilizes, and the period of the pendulum returns to its original value, which was determined by the length L.
Thus, after all the sand is drained, the period of the pendulum remains the same as it was initially. Therefore, the correct answer is:
(c) remains same.
Topper's Solved these Questions
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.4
2 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.5
2 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.2
2 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
Similar Questions
A simple pendulum is made of bob which is a hollow sphere full of sand suspended by means of a wire. If all the sand is drained out, the period of the pendulum will
View SolutionSuppose the bob in a simple pendulum is a hollow sphere with a small hole at the bottom. The sphere is filled with water and is made to oscillate. What happens to the period ?
View Solution
Knowledge Check
A uniform metallic rod rotates about its perpendicular bisector with constant angualr speed. If it is heated uniformly to raise its temperature slightly, then a) its speed of rotation increases b) its speed of rotation decreases c) its speed of rotation remains same d) its speed increases because its moment of inertia increases
Aits speed of rotation increasesBits speed of rotation decreasesCits speed of rotation remains sameDits speed increases because its moment of inertia increases
The time period of a simple pendulum is 2s. If its length is increased by 4 times, then its period becomes
(a) 16s (b) 12s (c) 8s (d) 4s
View SolutionA simple pendulum is made of a hollow sphere having a small hole in the bottom. The pendulum is made to vibrate after filling it with water.
STATEMENT -1 : Time period of pendulum will first increase upto certain maximum value and then decrease are return to its initial minimum value.
and
STATEMENT-2 : The effective length of osciallation of a simple pendulum first increases andthen decreases toreturn to its initial minimum value
View SolutionA hollow sphere is taken as bob of a simple pendulum. This hollow sphere is filled with fine sand. There is a small hole at the bottom of this sphere through which the fine sand leaks out. How does the time period of this simple pendulum alter? Discuss.
View SolutionA simple pendulum with a metallic bob has a time period T.The bob is now immersed in a non-viscous liquid and oscillated . If the density of the liuid is 14 that of metal , what will be the time period of the same pendulum?
Hint : If the solid bob of the pendulum has relative densty D and has been submerged in a non-viscous liquid of relative density ρ then effective acceleration due to gravity g'=g−gn where n=Dρ
View SolutionAssertion : The bob of a simple pendulum is a ball full of water, if a fine hole is made in the bottom of the ball, the time period first increases and then decreases.
Reason : As water flows out of the bob the weight of bob decreases.
View SolutionAssertion: If bob of a simple pendulum is kept in a horizontal electric field, its period of oscillation will remain same.
Reason: If bob is charged and kept in horizontal electric field, then the time period will be decreased.
View SolutionThe period of a simple pendulum whose bob is hollow metallic sphere is T. The period is T1 when the bob is filled with sand, T2 where it is filled with mercury and T3 when it is half filled with mercury Which of the following is true?
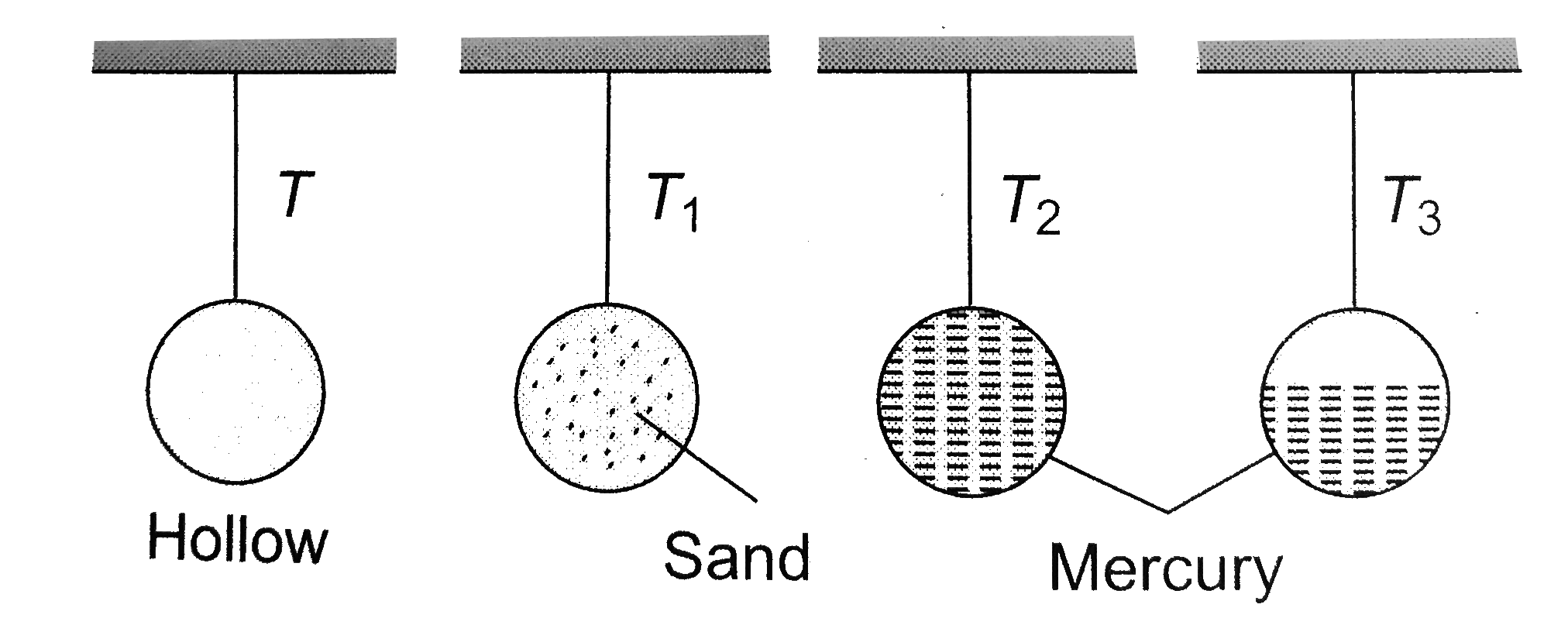
View Solution
