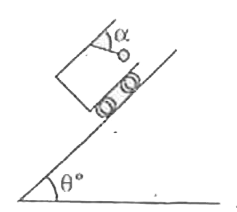
A simple pendulum is suspended from the ceiling of trolley which is sliding down on a inclined plane of inclination θ Find the angle made by the string with normal to the trolley a) when trolley slides down with uniform velocity b) when the plane is smooth.
To solve the problem, we need to analyze the forces acting on the pendulum bob in both scenarios: when the trolley is sliding down with uniform velocity and when the inclined plane is smooth.
Step 1: Analyze the first scenario (trolley sliding down with uniform velocity)
1. Understanding the situation: When the trolley slides down with uniform velocity, it means that the acceleration of the trolley is zero (a = 0). Therefore, the pendulum bob will experience no net force in the direction of the incline.
2. Draw the forces: The forces acting on the pendulum bob are:
- The gravitational force (mg) acting vertically downward.
- The tension (T) in the string acting along the string.
3. Identify the angles:
- Let θ be the angle of inclination of the plane with the horizontal.
- The angle made by the string with the vertical (normal to the trolley) will be α.
- Since the trolley is not accelerating, the pendulum will align itself such that the angle α = θ.
4. Conclusion for the first scenario:
- Therefore, the angle made by the string with the normal to the trolley is:
α=θ
Step 2: Analyze the second scenario (smooth inclined plane)
1. Understanding the situation: In this case, the trolley is accelerating down the incline due to gravity. The acceleration of the trolley is given by a=gsin(θ).
2. Draw the forces: The forces acting on the pendulum bob are:
- The gravitational force (mg) acting vertically downward.
- The tension (T) in the string acting along the string.
3. Resolve the forces:
- The gravitational force can be resolved into two components:
- Perpendicular to the incline: mgcos(θ)
- Parallel to the incline: mgsin(θ)
4. Set up the equations:
- The tension in the string must balance the forces acting on the pendulum bob.
- In the direction parallel to the incline, we have:
Tsin(α)=mgsin(θ)−ma
- Since a=gsin(θ), we substitute:
Tsin(α)=mgsin(θ)−mgsin(θ)=0
- This implies that:
Tsin(α)=0
- Since tension cannot be zero, we conclude that:
sin(α)=0⟹α=0∘
5. Conclusion for the second scenario:
- Therefore, the angle made by the string with the normal to the trolley is:
α=0∘
Final Answers:
a) When the trolley slides down with uniform velocity: α=θ
b) When the plane is smooth: α=0∘
2. Draw the forces: The forces acting on the pendulum bob are:
- The gravitational force (mg) acting vertically downward.
- The tension (T) in the string acting along the string.
- Let θ be the angle of inclination of the plane with the horizontal.
- The angle made by the string with the vertical (normal to the trolley) will be α.
- Since the trolley is not accelerating, the pendulum will align itself such that the angle α = θ.
- Therefore, the angle made by the string with the normal to the trolley is:
α=θ
- The gravitational force (mg) acting vertically downward.
- The tension (T) in the string acting along the string.
- The gravitational force can be resolved into two components:
- Perpendicular to the incline: mgcos(θ)
- Parallel to the incline: mgsin(θ)
- The tension in the string must balance the forces acting on the pendulum bob.
- In the direction parallel to the incline, we have:
Tsin(α)=mgsin(θ)−ma
- Since a=gsin(θ), we substitute:
Tsin(α)=mgsin(θ)−mgsin(θ)=0
- This implies that:
Tsin(α)=0
- Since tension cannot be zero, we conclude that:
sin(α)=0⟹α=0∘
- Therefore, the angle made by the string with the normal to the trolley is:
α=0∘
a) When the trolley slides down with uniform velocity: α=θ
b) When the plane is smooth: α=0∘
Similar Questions
A pendulum is hanging from the ceiling of a trolley which moves down a smooth inclined plane. Then
View SolutionA simple pendulum of length l is suspended from the celing of a cart which is sliding without friction on as inclined plane of inclination theta . What will be the time period of the pendulum?
View SolutionA simple pendulum of length l is suspended from the celing of a cart which is sliding without friction on as inclined plane of inclination theta . What will be the time period of the pendulum?
View SolutionA simple pendulum of length 5 m is suspended from the ceiling of a cart. Cart is sliding down on a frictionless surface having angle of inclination 60°. The time period of the pendulum is
View SolutionDerive an expression for the acceleration of a body sliding down a rough inclined plane.
View SolutionWhen a body rolls without sliding up an inclined plane the frictional force is :
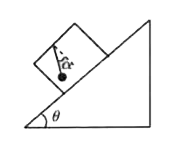
View SolutionA trolley is falling freely on inclined plane as shown in the figure. The angle of string of pendulum with the ceiling of trolley is (α) equal to
View SolutionA pendulum of mass m and length l is suspended from the ceiling of a trolley which has a constant acceleration a in the maximum deflection θ of the pendulum from the vertical.

View SolutionA pendulum of mass m hangs from a support fixed to a trolley which is moving up to the inclined plane with uniform acceleration 'a'. The angle which the string makes with vertical in equilibrium is

View SolutionA block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction

View Solution
