A pendulum of mass m hangs from a support fixed to a trolley. The direction of the string when the trolley rolls up a plane of inclination α with acceleration a0 is

θ=tan−1α
θ=tan1(a0g)
θ=tan1(ga0)
θ=tan1(a0+gsinαgcosα)
The correct Answer is:D
As in fig.
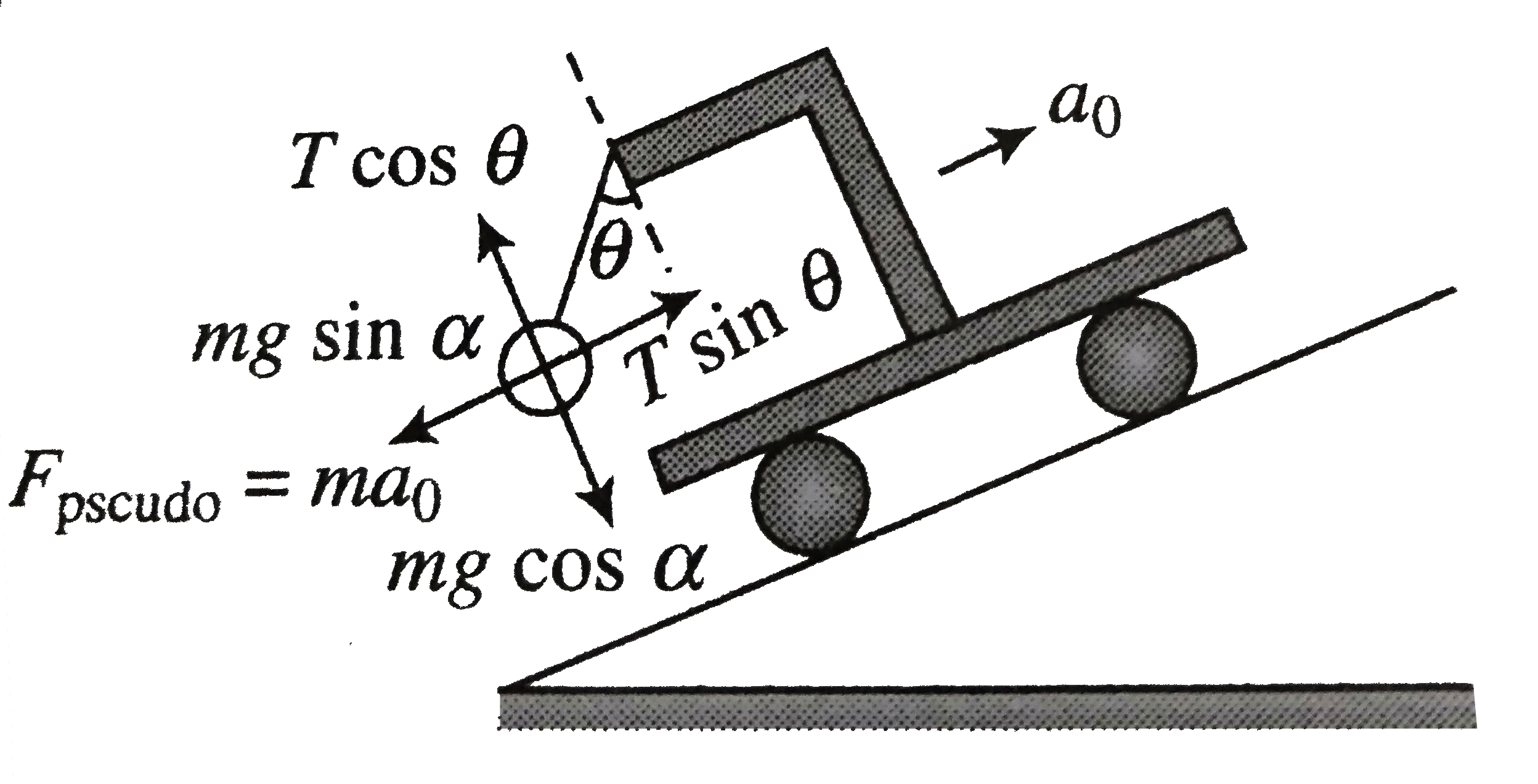
Tsinθ=ma0+mgsinα
Tcosθ=mgcosα
tanθ=a0+gsinαgcosθ.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective
15 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
A (trolley + child) of total mass 200 kg is moving with a uniform speed of 36 km/h on a frictionless track. The child of mass 20 kg starts running on the trolley from one end to the other (10 m away) with a speed of 10 ms–1 relative to the trolley in the direction of the trolley's motion and jumps out of the trolley with the same relative velocity. What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?
View SolutionA block B is m kept on an inclined plane. Anotherblock A is inserted in a slot in the block B though a light string. One end of the string is fixed to a support and other end of the string is attached to A. All the surfaces are smooth. Masses of A and B are same. The acceleration of block B is found to be 4/n.Find value of n.

View Solution
Knowledge Check
A pendulum of mass m hangs from a support fixed to a trolley which is moving up to the inclined plane with uniform acceleration 'a'. The angle which the string makes with vertical in equilibrium is
 A0Btan−1αCtan−1(a+gsinαgcosα)Dtan−1(acosαg+asinα)
A0Btan−1αCtan−1(a+gsinαgcosα)Dtan−1(acosαg+asinα)A pendulum has a ball of mass m attached to the stringa and is suspended from the roof of a trolley. If the trolley rolls upwards with acceleration a, then what is the angle made by the string with the inclined plane? (Given that, a=5m/s2,g=10m/s2 and the angle of inclination of the plane is 30∘)
Acos−1(2√3)Bcot−1(2√3)Csin−1(2√3)Dtan−1(2√3)A pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration 'a' the tension in the string is T1.When the elevator moves down with the same acceleration, the tension in the string is T1 .If the elevator were stationary, the tension in the string would be
AT1+T22B√T1+T2CT1T2T1+T2D2T1T3T1+T2
A body of mass M is hanging by an inextensible string of mass m. If the free end of the string accelerates up with constant acceleration a. find the variation of tension in the string a fuction of the distance measured from the mass M (bottom of the string).

View SolutionA pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration 'a' the tension in the string is T1. When the elevator moves down with the same acceleration, the tension in the string is T2. If the elevator were stationary, the tension in the string would be
View SolutionA trolley has a simple pendulum suspended from a frame fixed to itsa desk A block B is in contact on its vertical and The trolley is on horizontal rails and acceleration toward the right such that the block is just orevented from falling The value of coefficient of friction between A and B is 0.5 to the vertical is
View SolutionA body of mass m is placed over a smooth inclined plane of inclination θ, which is placed over a lift which is moving up with an acceleration a0 . Base length of the inclined plane is L. Calculate the velocity of the block with respect to lift at the bottom, if it is allowed to slide down from the top of the plane from rest :-
View SolutionA solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View Solution
