A simple pendulum is suspended from the roof of a trolley which moves in a horizontal direction with an acceleration α, then the time period is given by T=2π√(IT) where g is equal to
g
g-a
g+a
√g2+a2
The correct Answer is:D
(d) g'=√g2+a2
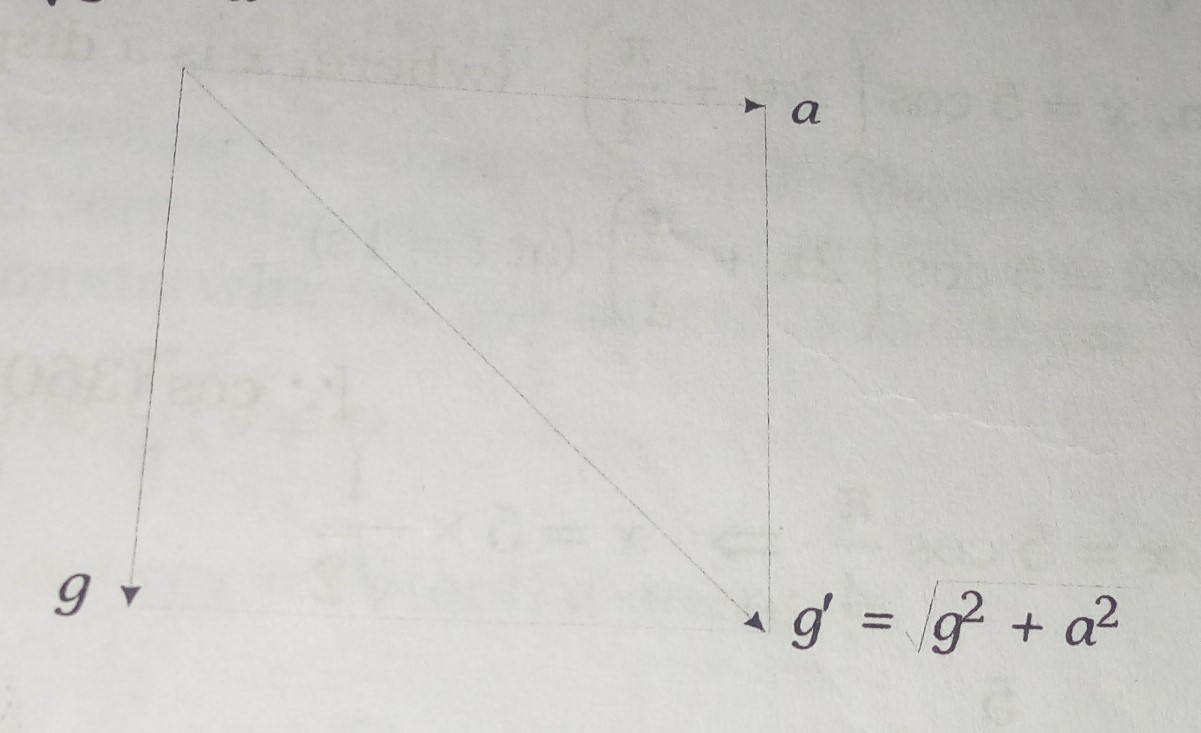
Similar Questions
The period of oscillation of a simple pendulum of length L suspended from the roof of a vehicle which moves without frication down on inclined plane of inclination lpha=60∘ is given by π√XLg then find X.
View SolutionA simple pendulum is hanging from the roof of a trolley which is moving horizontally with acceleration g. If length of the string is L and mass of the bob is m, then time period of oscillation is
View Solution
Knowledge Check
A simple pendulum of length L is suspended from the roof of a train. If the train moves in a horizontal direction with an acceleration 'a' then the period of the simple pendulum is given by
AT=2π√lgBT=2π√lg+aCT=2π√l(g2+a2)DT=2π√lg−aA simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal acceleration a.
AThe string makes an angle of tan−1(a/g) with the verticalBThe string makes an angle of tan−1(1−ag) with the verticalCThe tension in the string is m√a2+g2DThe tension in the string is m√g2−a2A simple pendulum with a bob of mass m is suspended from the roof of a car moving with horizontal acceleration a
AThe string makes an angle of tan−1(a/g) with the verticalBThe string makes an angle of sin−1(ag) with the verticalCThe tension in the string is m√a2+g2DThe tension in the string is m√g2−a2
A seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4m/s2 . Its period of oscillation is
View SolutionA seconds pendulum is suspended form the roof of a lift. If the lift is moving up with an acceleration 9.8m/s2, its time period is
View SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal accelertion a. The angle made by the string with verical is
View SolutionTime period of simple pendulum suspended from a metallic wire
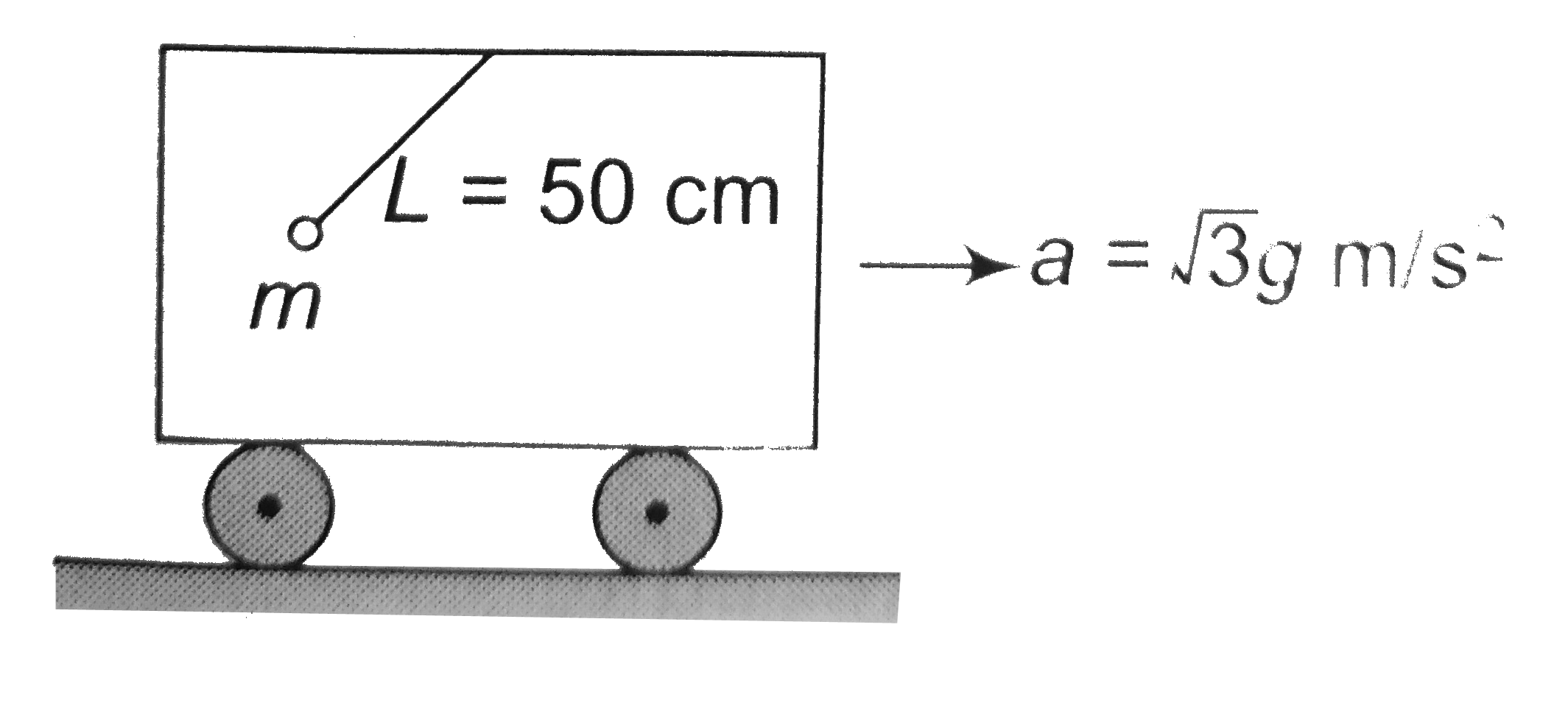
View SolutionA simple pendulum 50cm long is suspended from the roof of a acceleration in the horizontal direction with constant acceleration √3gm/s−1. The period of small oscillations of the pendulum about its equilibrium position is (g=π2m/s2) ltbRgt
View Solution
