A simple pendulum is hanging from the roof of a trolley which is moving horizontally with acceleration g. If length of the string is L and mass of the bob is m, then time period of oscillation is
2π√Lg√2
2π√2Lg
2π√L2g
2π√Lg
To find the time period of oscillation of a simple pendulum hanging from a trolley that is moving horizontally with an acceleration equal to g, we can follow these steps:
Step 1: Understand the Forces Acting on the Pendulum
When the trolley accelerates horizontally with acceleration g, the pendulum bob experiences two forces:
1. The gravitational force acting downward, mg.
2. The pseudo force acting horizontally in the opposite direction of the trolley's acceleration, which is ma where a=g.
Step 2: Determine the Effective Acceleration
The effective acceleration acting on the pendulum bob can be determined by considering the resultant of the gravitational force and the pseudo force. The gravitational force acts downward, and the pseudo force acts horizontally.
Using Pythagoras theorem, the effective acceleration aeff can be calculated as:
aeff=√g2+g2=√2g2=g√2
Step 3: Use the Formula for Time Period of a Pendulum
The time period T of a simple pendulum is given by the formula:
T=2π√Lgeff
where geff is the effective acceleration due to gravity.
Step 4: Substitute the Effective Acceleration
Substituting geff=g√2 into the time period formula, we get:
T=2π√Lg√2
Step 5: Simplify the Expression
This can be simplified as:
T=2π√Lg√2=2π√Lg⋅1√√2=2π√Lg⋅121/4
Final Result
Thus, the time period of oscillation of the pendulum is:
T=2π√Lg√2
When the trolley accelerates horizontally with acceleration g, the pendulum bob experiences two forces:
1. The gravitational force acting downward, mg.
2. The pseudo force acting horizontally in the opposite direction of the trolley's acceleration, which is ma where a=g.
The effective acceleration acting on the pendulum bob can be determined by considering the resultant of the gravitational force and the pseudo force. The gravitational force acts downward, and the pseudo force acts horizontally.
aeff=√g2+g2=√2g2=g√2
The time period T of a simple pendulum is given by the formula:
T=2π√Lgeff
where geff is the effective acceleration due to gravity.
Substituting geff=g√2 into the time period formula, we get:
T=2π√Lg√2
This can be simplified as:
T=2π√Lg√2=2π√Lg⋅1√√2=2π√Lg⋅121/4
Thus, the time period of oscillation of the pendulum is:
T=2π√Lg√2
Topper's Solved these Questions
Similar Questions
A simple pendulum is suspnded from the ceilignof a car accelerating uniformly on a horizontal road.If the acceleration is a0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.
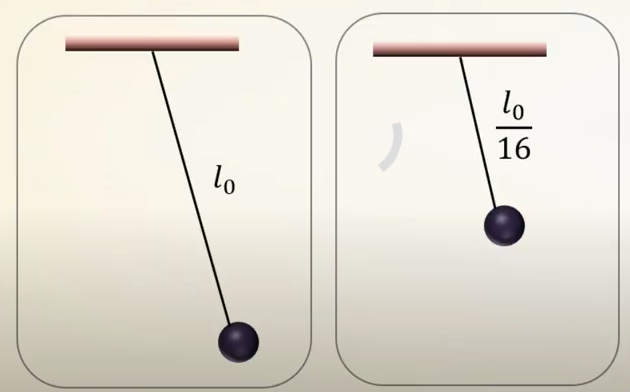
View SolutionA simple pendulum of length l0 can perform simple harmonic oscillations with a time period T0. If the length of the pendulum is decreased to l016 then the time time period of oscillation will become.
View Solution
Knowledge Check
A simple pendulum with a bob of mass m is suspended from the roof of a car moving with horizontal acceleration a
AThe string makes an angle of tan−1(a/g) with the verticalBThe string makes an angle of sin−1(ag) with the verticalCThe tension in the string is m√a2+g2DThe tension in the string is m√g2−a2A simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal acceleration a.
AThe string makes an angle of tan−1(a/g) with the verticalBThe string makes an angle of tan−1(1−ag) with the verticalCThe tension in the string is m√a2+g2DThe tension in the string is m√g2−a2A seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4m/s2 . Its period of oscillation is
A1.90sB1.70sC2.30sD1.40s
A simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal accelertion a. The angle made by the string with verical is
View SolutionA simple pendulum is suspended from the roof of a trolley which moves in a horizontal direction with an acceleration α, then the time period is given by T=2π√(IT) where g is equal to
View SolutionA simple pendulum of length L is suspended from the roof of a train. If the train moves in a horizontal direction with an acceleration 'a' then the period of the simple pendulum is given by
View SolutionThe time period of oscillation of a simple pendulum having length Land mass off the bob mis given as T. Ifthe length of the pendulum is increased to 4L and the mass of the bob is increased to 2m, then which one of the following is the new period of oscillation?
View SolutionThe periodic time of a simple pendulum is 3 sec. The mass of its hollow spherical bob is 100 gram. The bob is then filled with sand, so that the mass of the bob becomes 200 gram. Then the new period of oscillation of the simple pendulum wil be
View Solution
