A simple pendulum length l with a bob of mass m is taken into Earth orbit on the International space station. What is its frequency of oscillation with respect to that on the ground?
To solve the problem of determining the frequency of oscillation of a simple pendulum taken to the International Space Station (ISS) compared to its frequency on the ground, we can follow these steps:
Step 1: Understand the formula for the frequency of a simple pendulum
The frequency f of a simple pendulum is given by the formula:
f=12π√gL
where:
- g is the acceleration due to gravity,
- L is the length of the pendulum.
Step 2: Determine the value of g on the ground
On the surface of the Earth, the value of g is approximately 9.81m/s2. Therefore, the frequency of the pendulum on the ground can be calculated as:
fground=12π√9.81L
Step 3: Analyze the situation in orbit
When the pendulum is taken to the ISS, it is in a state of free fall. In this condition, the effective acceleration due to gravity g becomes negligible (close to zero) because both the pendulum and the ISS are in free fall around the Earth. Thus, we can approximate:
gorbit≈0m/s2
Step 4: Calculate the frequency in orbit
Using the formula for frequency with g in orbit:
forbit=12π√gorbitL=12π√0L=0
This means that the frequency of oscillation of the pendulum in the ISS is 0Hz.
Conclusion
The frequency of oscillation of the simple pendulum in the International Space Station is 0Hz, indicating that it does not oscillate in a microgravity environment.
---
The frequency f of a simple pendulum is given by the formula:
f=12π√gL
where:
- g is the acceleration due to gravity,
- L is the length of the pendulum.
On the surface of the Earth, the value of g is approximately 9.81m/s2. Therefore, the frequency of the pendulum on the ground can be calculated as:
fground=12π√9.81L
When the pendulum is taken to the ISS, it is in a state of free fall. In this condition, the effective acceleration due to gravity g becomes negligible (close to zero) because both the pendulum and the ISS are in free fall around the Earth. Thus, we can approximate:
gorbit≈0m/s2
Using the formula for frequency with g in orbit:
forbit=12π√gorbitL=12π√0L=0
This means that the frequency of oscillation of the pendulum in the ISS is 0Hz.
The frequency of oscillation of the simple pendulum in the International Space Station is 0Hz, indicating that it does not oscillate in a microgravity environment.
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Very Short Answer Questions
99 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Short Answer Questions
104 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - SOLVED EXAMPLES
54 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
Polar satellites : Medium earth orbits : : International space station : ………………
View SolutionA simple pendulum of length l and with a bob of mass m moving alon a circular are of angle θ in a vertical plane. A sphere of mass m is placed at the end of the circular arc. What momentum will be given to the sphere by the moving bob?
View Solution
Knowledge Check
A simple pendulum of length l and bob of mass m is displaced from its equilibrium position O to a position P so that height of P above O is h . If is then released. What is the tension in the string when the bob passes through the through the equilibrium position O ? Neglect friction. v is the velocity of the bob at O
Am(g+v2l)B2mghlCmg(1+hl)Dmg(1+2hl)A simple pendulum with a bob of mass m oscillates from A to C and back to A such that PB is H. If the acceleration due to gravity is g, then the velocity of the bob as it passes through B is
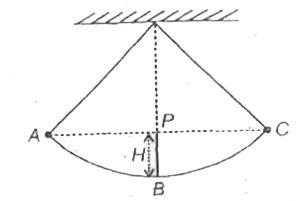 AmgHB√2gHCZeroD2gH
AmgHB√2gHCZeroD2gHa simple pendulum with a bob of mass m savings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the strings is-
Aless than mg cos 20∘Bgreater than mg cos 20∘Cequal to mg cos 20∘Dunpredictable
A simple pendulm has a length L and a bob of mass M. The bob is vibrating with amplitude a .What is the maximum tension in the string?
View SolutionSuppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
View SolutionA simple pendulum with a bob of mass m oscillates from A to C and back to A, such that PB=h,
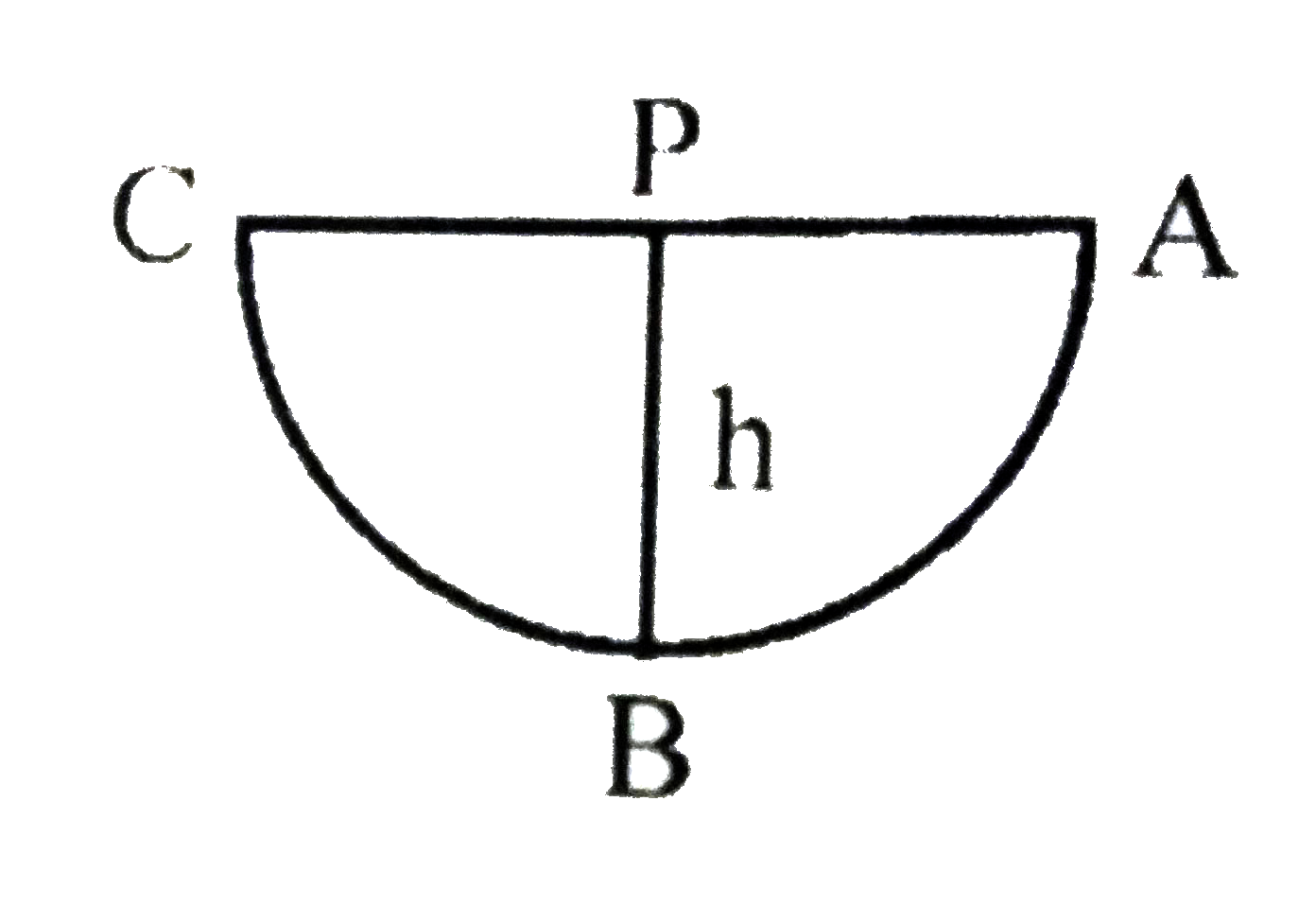
If the acceleration due to gravity is 'g', then the velocity of the bob as it passes through B is
View SolutionA lift having a simple pendulum attached with its ceiling is moving upward with constant acceleration 'a'. What will be the tension in the string of pendulum with respect to a boy inside the lift and a boy stansing on earth, mass of bob of simple pendulum is m.
View SolutionA simple pendulum of length 'l' and having bob of mass 'm' is doing angular SHM inside water A constant buoyant force equal to half the weight of he bob is acting on the ball. Find the time period of oscillation?
View Solution
