A simple pendulm has a length L and a bob of mass M. The bob is vibrating with amplitude a .What is the maximum tension in the string?
To find the maximum tension in the string of a simple pendulum with length L, mass M, and amplitude A, we can follow these steps:
Step 1: Understand the forces acting on the pendulum bob
When the pendulum bob is at any position, two main forces act on it:
- The gravitational force mg acting downward.
- The tension T in the string acting upward and towards the pivot.
Step 2: Analyze the forces at the maximum tension point
The maximum tension occurs when the bob is at the lowest point of its swing (mean position). At this point, the gravitational force and the centripetal force due to the circular motion must be considered.
Step 3: Write the equation for tension
At the lowest point, the tension can be expressed as:
T=mg+mv2L
where:
- T is the tension in the string,
- mg is the weight of the bob,
- mv2L is the centripetal force required to keep the bob moving in a circular path.
Step 4: Determine the velocity at the lowest point
To find the maximum velocity v of the bob at the lowest point, we can use energy conservation. The potential energy at the maximum height (amplitude A) is converted into kinetic energy at the lowest point.
The potential energy at the maximum height is:
PE=mgh=mgA
At the lowest point, all this potential energy converts into kinetic energy:
KE=12mv2
Setting these equal gives:
mgA=12mv2
Solving for v2:
v2=2gA
Step 5: Substitute v2 back into the tension equation
Now, substitute v2 into the tension equation:
T=mg+m(2gA)L
This simplifies to:
T=mg+2mgAL
Step 6: Factor out mg
Factoring out mg gives:
T=mg(1+2AL)
Conclusion
Thus, the maximum tension in the string of the pendulum is:
Tmax=mg(1+2AL)
---
When the pendulum bob is at any position, two main forces act on it:
- The gravitational force mg acting downward.
- The tension T in the string acting upward and towards the pivot.
The maximum tension occurs when the bob is at the lowest point of its swing (mean position). At this point, the gravitational force and the centripetal force due to the circular motion must be considered.
At the lowest point, the tension can be expressed as:
T=mg+mv2L
where:
- T is the tension in the string,
- mg is the weight of the bob,
- mv2L is the centripetal force required to keep the bob moving in a circular path.
To find the maximum velocity v of the bob at the lowest point, we can use energy conservation. The potential energy at the maximum height (amplitude A) is converted into kinetic energy at the lowest point.
PE=mgh=mgA
At the lowest point, all this potential energy converts into kinetic energy:
KE=12mv2
Setting these equal gives:
mgA=12mv2
Solving for v2:
v2=2gA
Now, substitute v2 into the tension equation:
T=mg+m(2gA)L
This simplifies to:
T=mg+2mgAL
Factoring out mg gives:
T=mg(1+2AL)
Thus, the maximum tension in the string of the pendulum is:
Tmax=mg(1+2AL)
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - NCERT EXERCISES WITH SOLUTIONS
19 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Additional Exercises
6 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Long Answer Questions
33 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
A simple pendulum having a bob of mass m undergoes smasll oscillastions with amplitude θ0 Find the tension in the string as a function of the angle made by the string with the vertical. When in this tension maximum, and when is it minimum?
View SolutionA pendulum has length L = 1.8 m. The bob is released from position shown in the figure. Find the tension in the string when the bob reaches the lowest position. Mass of the bob is 1 kg.

View Solution
Knowledge Check
A simple pendulum has a string of length l and bob of mass m. When the bob is at its lowest position , it is given the minimum horizontal speed necessary for it to move in a circular path about the point point of suspension. The tension in the string at the lowest position if the bob is
A3mgB4mgC5mgD6mgA simple pendulam of length L carriers a bob of mass m. When the bob is at its lowest position, it is given the minimum horizontal speed necessary for it to move in a vertical circle about the point of suspension. When the string is horizontal the net force on the bob is
A√10mgB√5mgC4 mgD1 mgA simple pendulum has a bob of mass m and swings with an angular amplitude ϕ. The tension in thread is T. At a certain time the string makes an angle θ with the vertical (θ≤ϕ)
AT=mgcosθ for all value of θBT=mgcosθ for only θ=ϕCT=mg,forθ=cos−1[13(2cosϕ+1)]DT will be larger for smaller values of θ
A simple pendulum of length 1 m with a bob of mass m swings with an angular amplitude 30°. Then (g = 9.8 ms−2)
View SolutionA simple pendulum of length 'l' carries a bob of mass 'm'. If the breaking strength of the string is 3mg, the maximum angular amplitude from the vertical can be
View SolutionA simple pendulum of length 1 m with a bob of mass m swings with an angular amplitude 30∘. Then (g=9.8m/s2
View SolutionA simple pendulum is oscillating with an angular amplitude 60∘. If mass of bob is 50 gram, then the tension in the string at mean position is (g=10ms−2)
View SolutionA simple pendulum has a length l & mass of bob m. The bob is given a charge q coulomb. The pendulum is suspended in a uniform horizontal electric field of strength E as shown in figure, then calculate the time period of oscillation when bob is slightly displaced from its mean position.
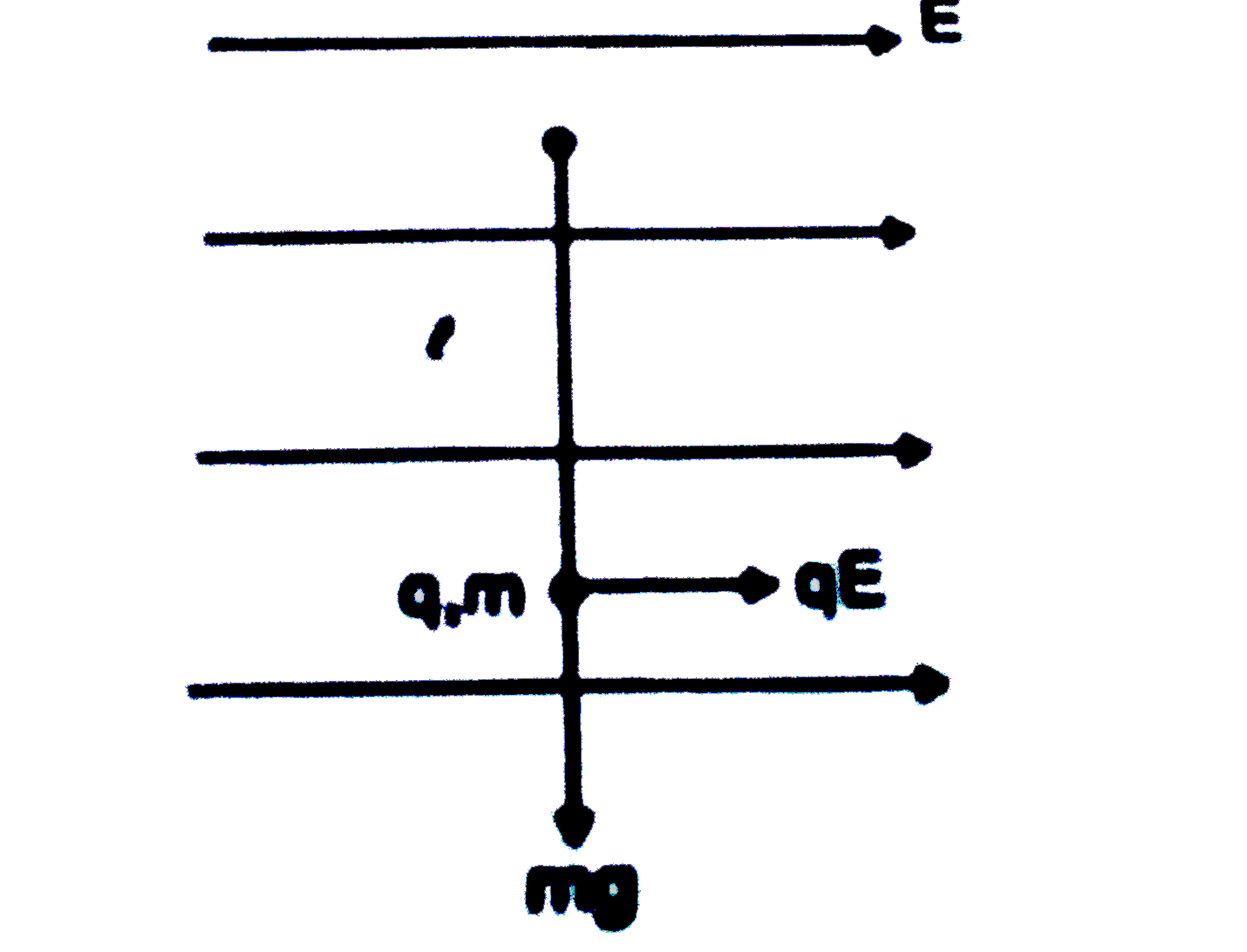
View Solution
