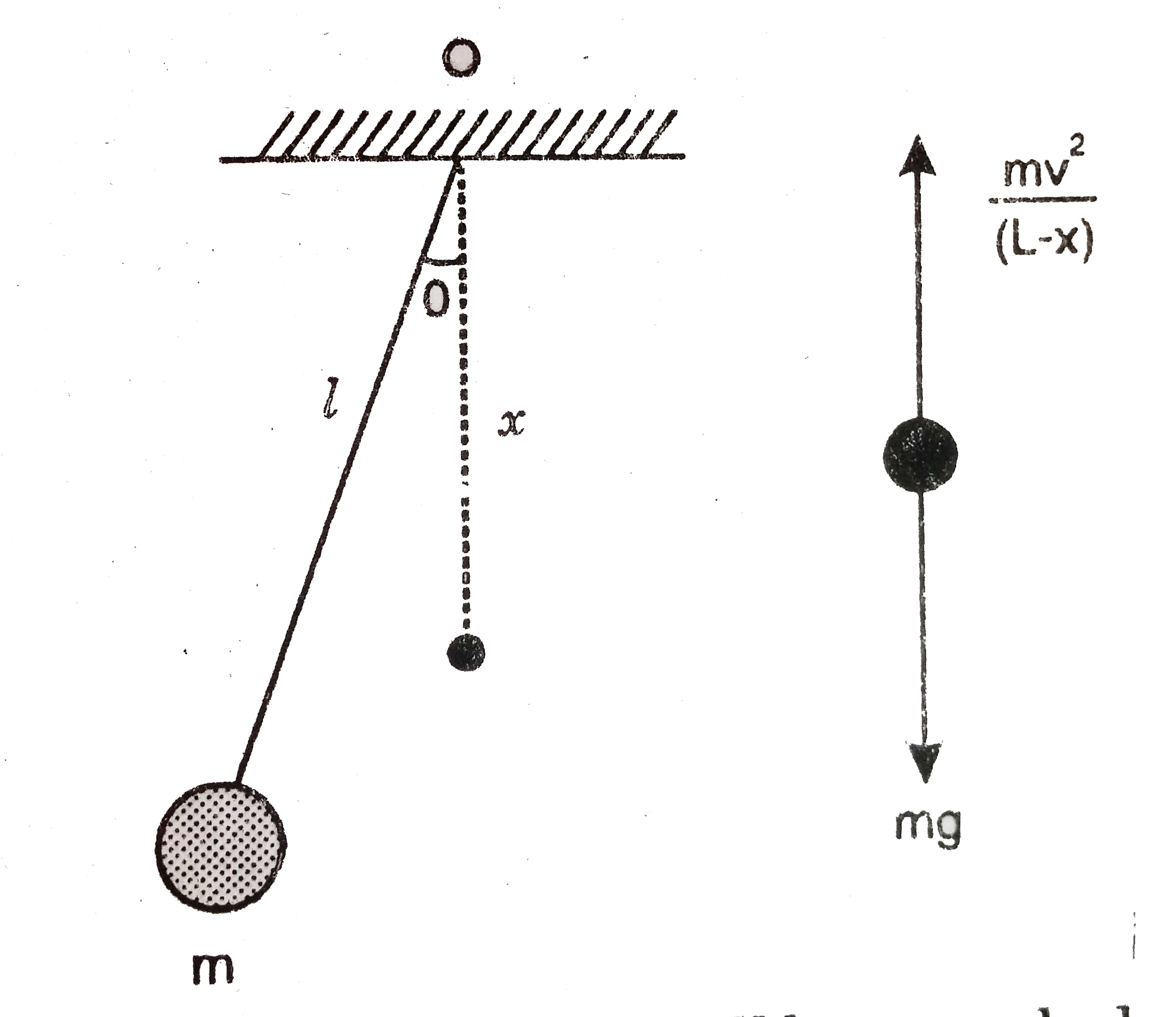
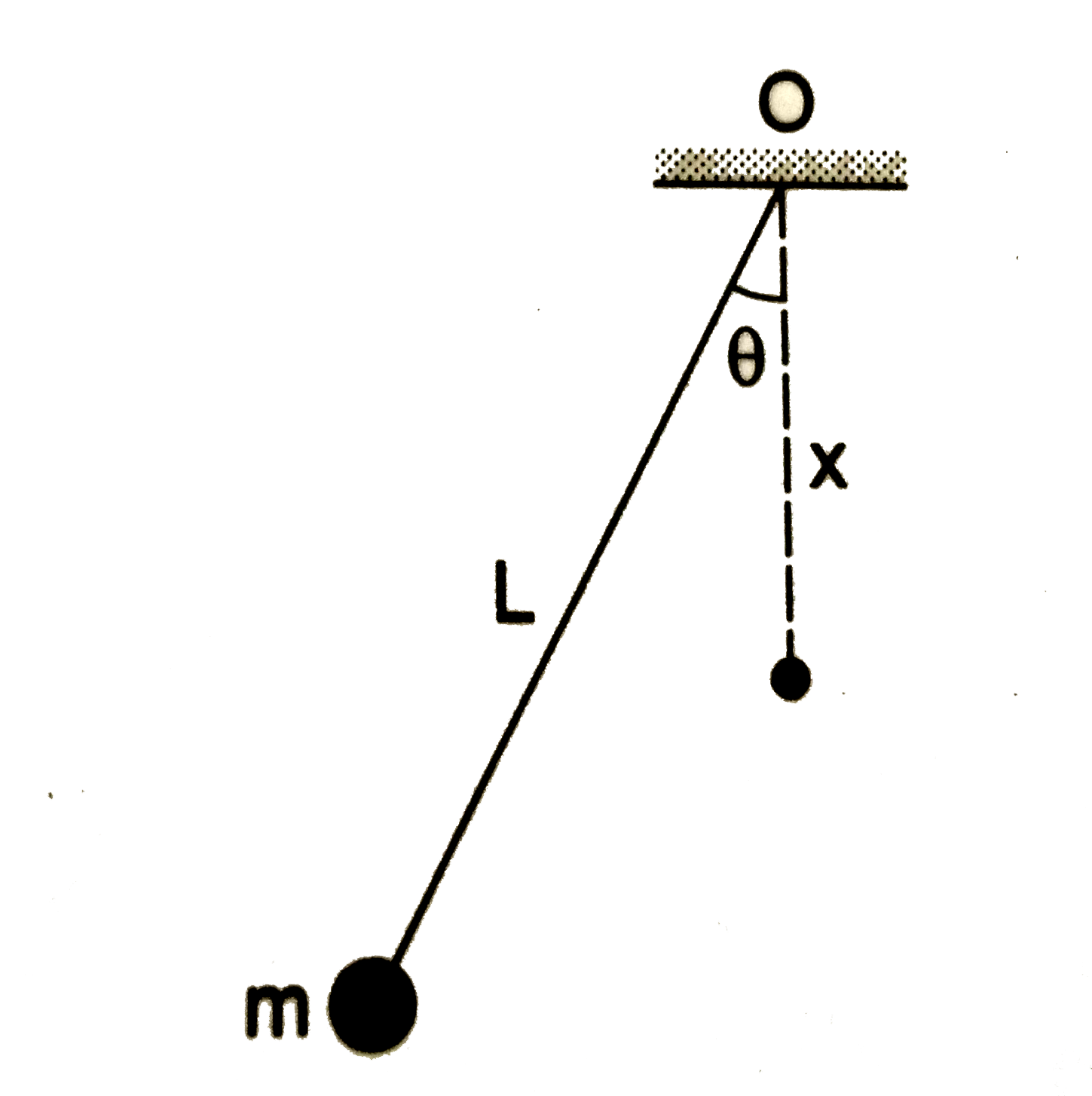
A simple pendulum of length L having a bob of mass m is deflected from its rest position by an angle θ and released figure. The string hits a peg which is fixed at distance x below the point of suspension and the bob starts going in a circle centred at the peg. a. Assuming that initially the bob has a height less thasn the peg, show that the maximum height reached by the bob equals its initialheight. b. If the pendulum is released with θ=900 and m=L2 find the maximum height reached by the bob above its lowest positon before the string becomes slack. c. Find the minimum value of x/L for which the bob goes in a complete circle about the pet when the pendulum is released from θ=900.
 Solution in Tamil
Solution in Tamil
The correct Answer is:A, B, C
a. When the bob has an initial height less than the peg and the released from rest ure let body travels from A to B since, total energy at A
=Totale≠rgyatB,<br>:.(KE)_A+(PE)_A=(KE)_B+(PE)_B<br>rarr(PE)_=(PE)_A<br>∵(KE)A=(KE)_B=0<br>Sothemaxiμmheightreachedbythebobisequal→∈itialheight.<br>b.Whenthependu––misre≤asedwiththeta ==90^0 and x=l/2, ure the path of the particle is shown in ure.

At point C the string wil becomke slack and so the particle wil start making projectile motion.
Apply law of conservation.
(12)mv2c−0=mg(L2)(1−cosα)
[because distance between A and C ]
In the vertical direction is
L2=(1−cosα)
→V4c=gL(1−cosα)............i
Again, from the feebody diagram ure
mv2cL2=mgcosα......ii
[becuseTC=0]
From equation i and equation ii
gL(1−cosα)=gL2cosα
→1−cosα=12cosα
→32cosα=1
→cosα=(23)......iii
to find highest positon C1 before the string becomes slack.
BF=L2+L2cosθ
=L2+L2×23
=L(12+13)
So, BF=(5L6)
c. If the principle has to complete a vertical circle at the point C
mv2cL−x=mg.......i
Again applying energy principle between A and C
(12)mv2c−0=mg(OC)
→(12)mv2c=mg(L−2(l−x))
=mg(2x−L)
→v2c=2g(2x−L) .......ii
From equation i and ii
g(L−x)=2g(2x−L)
→L−x=4x−2L
→5x=3L
∴xL=35=0.6
So, the rates (xL) should be 0.6.
Topper's Solved these Questions
Similar Questions
A heavy stone is thrown from a cliff of height h with a speed v. The stone will hit the ground with maximum speed if it is thrown
View SolutionA wave pulse passing on a string with speed of 40cms−1 in the negative x direction has its maximum at x=0 at t=0. Where will this maximum be located at t=5s?
View SolutionA pendulum comprising a light string of length L and small sphere, swings in the vertical plane . The string hits a peg located a distance of bellow the point of suspension (figure). If the pendulum is released from rest at the horizontal possition (θ=90∘) and is to swing in a complete circule centered on the peg, the minimum value of d is

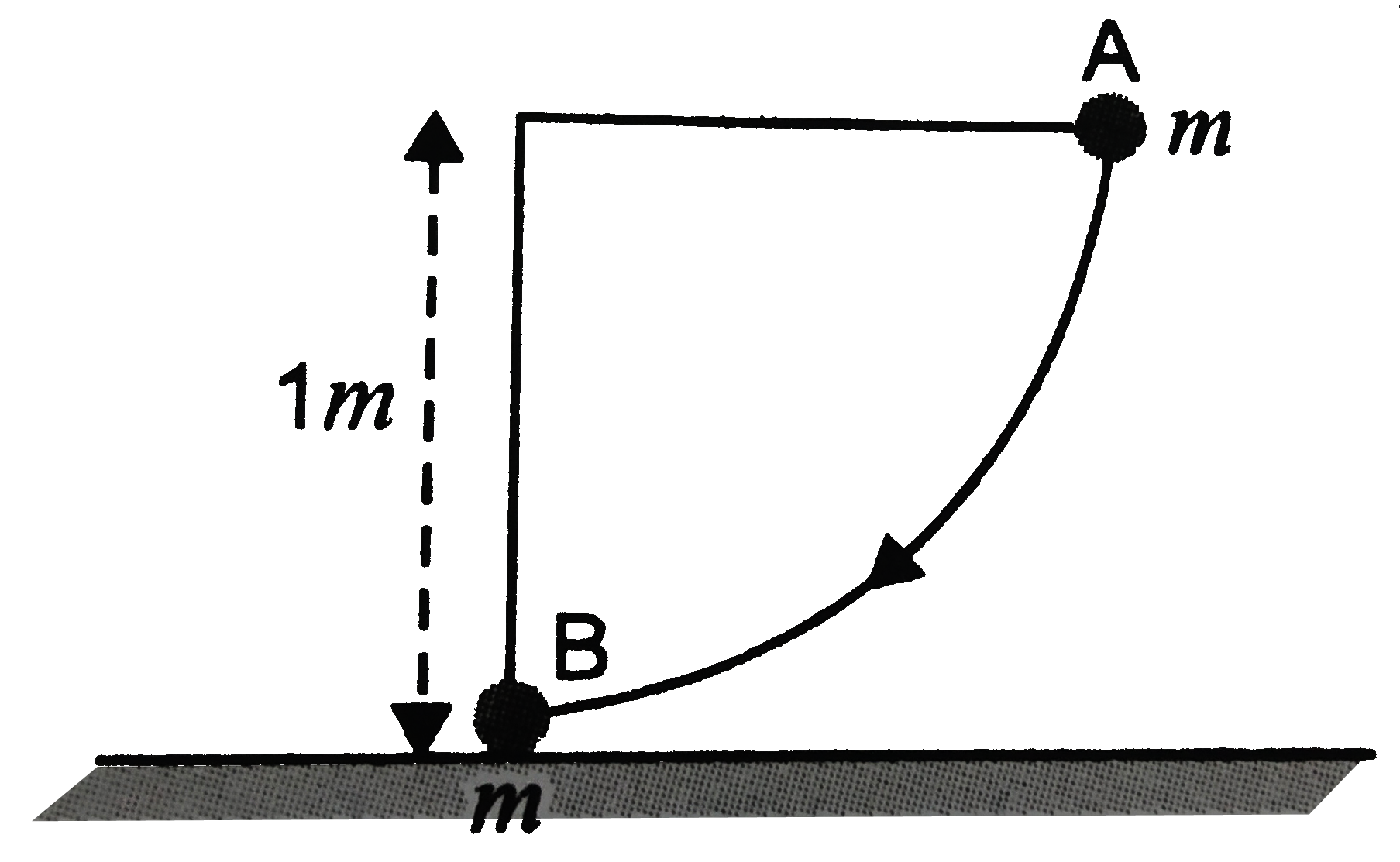
View SolutionThe bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.
View SolutionA nail is located at a certain distance vertically below the point of suspension of a simple pendulum. The pendulum bob is released from a position where the string makes an angle of 60^(@) with the vertical. Calculate the distance of nail from the point of suspension such that the bob will just perform revolutions with the nail as centre. Assume the length of the pendulum to be one meter.
View SolutionA simple pendulum of length L having a bob of mass m is first taken aside so that the string forms the tight angle with the verticle and then released. The string hits a peg which is fixed at a distance below the point of suspension and the bob starts going in a circle centered at the peg. find the minimum value of y for which the bob goes in a complete circle about the peg.

View SolutionA simple pendulum bob has a mass ''m'' and length ''L'' . The bob is drawn aside such that the string is horizontal and then it is released. The velocity of the bob while it crosses the equilibrium position is
View SolutionA nail is fixed at a point P vertically below the point of suspension 'O' of simple pendulum of length 1m. The bob is released when the string of pendulum makes an angle 30∘ with horiozontal. The bob reaches lowest point and then describes vertical circle whose centre coincides with P . The least distance of P from O is
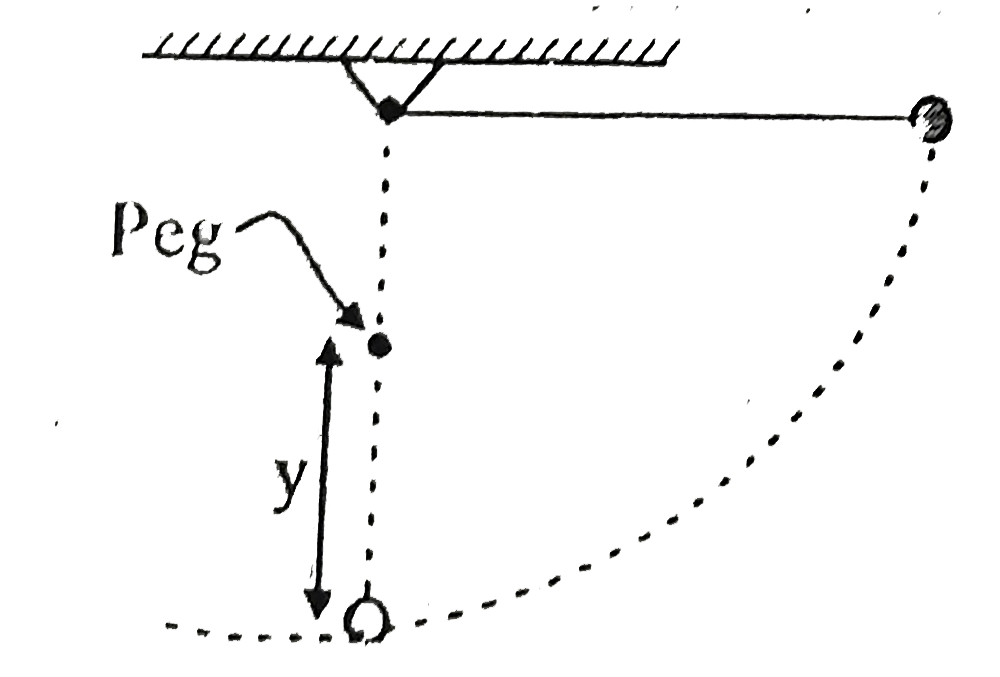
View SolutionA bob tied to an ideal string of length l is released from the horizontal position shown. A peg P whose height is adjustable, can arrest the free swing of the pendulum, as shown in Figure.
View SolutionA pendulum bob of mass m and length L is released from angle theta with the vertical. Find (a) the speed of the bob at the bottom of the swing and (b) tension in the string at that time
View SolutionThe figure shows a pendulum of length l suspended at a distance x vertically above a peg. (a) The pendulum bob is deflected through an angle theta and then released. Find the speed of the bob at the instant (b) The pendulum is released when theta = 90^(@) . For what x (position of peg) will the pendulum complete the circle ? (c) The pendulum is released when theta = 60^(@) . what is the velocity of the bob as it passes position E.
View SolutionA brass bob is suspended by an inextensible weightless string of length l from a peg fixed on a vertical wall. A nail is fixed in the wall at a distance d vertically below the point of suspension of the string. The bob is then drawn to a position where the string becomes horizontal and it is released from there. Show that d must be at least 0.6l if the bob is to swing completely around in a circle centred on the nail.
View SolutionL लंबाई वाले एक सरल दोलक के बॉब का द्रव्यमान m हैं । निलंबन - बिंदु से x से दूरी नीचे एक कील जड़ी हैं । दोलक को विराम स्थिति से θ कोण तक विस्थापित करके छोड़ दिया जाता हैं । डोरी उस कील से टकराती है और बॉब एक वृत्ताकार पथ तय करने लगता हैं जिसका केंद्र कील हैं ।
यह मानते हुए कि प्रारंभ में बॉब की ऊँचाई कील से कम थी , दिखाइए कि बॉब को प्राप्त होने वाली अधिकतम ऊँचाई इसकी प्रारंभिक ऊँचाई के बराबर होगी ।
View SolutionThe bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure. If the length of the pendulum is 1m, calculate (a) the height to which bob A will rise after collision. (b) the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.
View SolutionA nail is located below the point of suspension of a simple pendulum of length l . The bob is released from horizontal position. If the bob loops a verticle circle with nail as centre, find the distance of nail from point of suspension.
View SolutionA nail is located below the point of suspensions of a simple pendlum of length .l.. The bob is released from horizontal position. If the bob loops a verticle circle with nail as centre, find the distance of nail from point of suspension.
View Solution
