A sinusoidal transverse wave of amplitude 10−2 m, wavelength λ, frequency f is travelling with speed (V = 20 m/s) on a stretched string. If the maximum speed at any point of the string is V5 then find the frequency and wavelength of the wave.
To solve the problem step by step, we will follow the concepts of wave motion and the relationships between amplitude, frequency, wavelength, and wave speed.
Step 1: Understand the given parameters
We are given:
- Amplitude (A) = 10−2 m
- Speed of the wave (V) = 20 m/s
- Maximum speed at any point of the string = V/5
Step 2: Relate maximum speed to angular frequency
The maximum speed (Vmax) of a point on a wave is given by the formula:
Vmax=A⋅ω
where A is the amplitude and ω is the angular frequency.
Step 3: Substitute the given maximum speed
We know that the maximum speed is also given as V/5:
Vmax=V5=205=4 m/s
Now, we can set the two expressions for maximum speed equal to each other:
A⋅ω=4
Step 4: Substitute the amplitude
Substituting the value of amplitude:
10−2⋅ω=4
Now, solve for ω:
ω=410−2=400 rad/s
Step 5: Relate angular frequency to frequency
The angular frequency ω is related to the frequency f by the formula:
ω=2πf
Substituting for ω:
400=2πf
Step 6: Solve for frequency
Now, solve for f:
f=4002π=200π Hz
Step 7: Calculate the wavelength
The wavelength λ can be calculated using the formula:
λ=Vf
Substituting the values of V and f:
λ=20200π=20⋅π200=π10 m
Final Answers
- Frequency f=200π Hz
- Wavelength λ=π10 m
We are given:
- Amplitude (A) = 10−2 m
- Speed of the wave (V) = 20 m/s
- Maximum speed at any point of the string = V/5
The maximum speed (Vmax) of a point on a wave is given by the formula:
Vmax=A⋅ω
where A is the amplitude and ω is the angular frequency.
We know that the maximum speed is also given as V/5:
Vmax=V5=205=4 m/s
Now, we can set the two expressions for maximum speed equal to each other:
A⋅ω=4
Substituting the value of amplitude:
10−2⋅ω=4
Now, solve for ω:
ω=410−2=400 rad/s
The angular frequency ω is related to the frequency f by the formula:
ω=2πf
Substituting for ω:
400=2πf
Now, solve for f:
f=4002π=200π Hz
The wavelength λ can be calculated using the formula:
λ=Vf
Substituting the values of V and f:
λ=20200π=20⋅π200=π10 m
- Frequency f=200π Hz
- Wavelength λ=π10 m
Topper's Solved these Questions
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - REVISION EXERCISES
107 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - MULTIPLE CHOICE QUESTIONS
88 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - NCERT EXEMPLAR PROBLEMS
31 Videos
- UNITS AND MEASUREMENTBOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - CHAPTER PRACTICE TEST
15 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Chapter Practice Test
16 Videos
Similar Questions
A transverse wave of amplitude 2 m, wavelength 4 m and frequency 6 Hz is propagating in a string toward positive y-direction. The equation of the wave may be (y is in m and t is in s)
View SolutionFor the wave shown in the figure, the frequency and wavelength if its speed is 320 m/s are
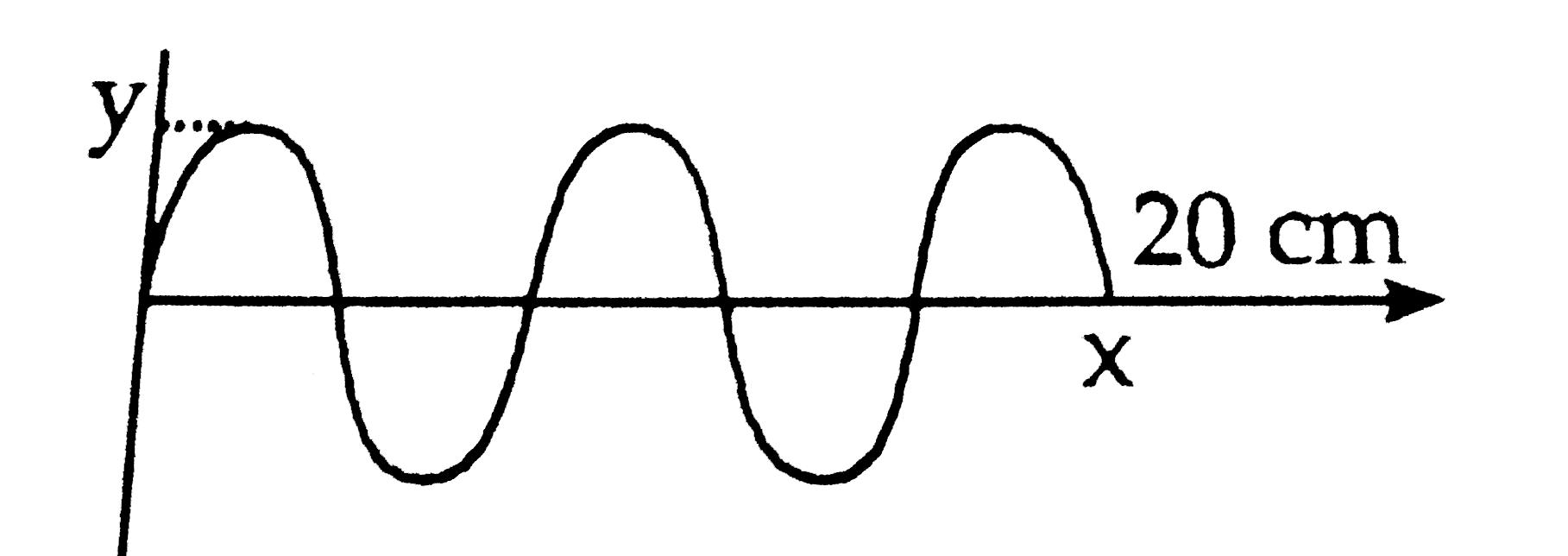
View Solution
Knowledge Check
A transverse sinusoidal wave of amplitude A, wavelength λ and frequency f is travelling along a stretch string. The maximum speed of any point on the string is v10, where, V is the velocity of wave propagation. If A=10−3m,andV=10ms−1, then λ and f are given by
Aλ=2π×10−2mBλ=10−2mCf=1032πHzDf=104HzA transverse sinusoidal wave of amplitude a, wavelength λ and frequency f is travelling on a stretched string. The maximum speed of any point in the string is v/10, where v is the speed of propagation if the wave. If a=10−3m and v=10ms−1, then lanbda and f are given by
A(a) λ=2π×10−2mB(b) λ=10−3mC( c ) f=103Hz/(2π)D(d) f=104HzA transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is [
Ay(x,t)=0.5sin(2πx−4πt)By(x,t)=0.5cos(2πx+4πt)Cy(x,t)=0.5sin(πx+2πt)Dy(x,t)=0.5cos(2πx+2πt)
A transverse wave, whose amplitude is 0.5 m wavelength is 1 m and frequency is 2Hz. is travelling along positive x direction. The equation of this wave will be-
View SolutionA transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is
View SolutionSpeed (v), wavelength (λ) and the frequency (f) of sound are related as
View SolutionIf the speed of a transverse wave on a stretched string of length 1 m is 60ms−1, what is the fundamental frequency of vibration ?
View SolutionA sinusoidal transverse wave is traveling on a string. Any point on the string
View Solution
