A skater rotating about a vertical axis pulls her arms inward. Ignoring all frictional effects, which of the following statements are true? Denote the magnitude of her angular velocity by ω, the magnitude of her angular momentum by L, and her kinetic energy by Ek.
L is constant, Ek increases
L is constant, ω increases
L and Ek are both constant
L and ω are both constant
The correct Answer is:A, B
To solve the problem regarding the skater rotating about a vertical axis while pulling her arms inward, we will analyze the situation step by step, focusing on the conservation of angular momentum, the relationship between angular momentum and angular velocity, and the effect on kinetic energy.
1. Understanding Angular Momentum Conservation:
- The skater is rotating about a vertical axis and pulls her arms inward. Since we are ignoring all frictional effects, there are no external torques acting on the skater. Therefore, the angular momentum (L) of the system is conserved.
- Conclusion: L=constant
2. Relationship Between Angular Momentum and Angular Velocity:
- The angular momentum (L) is related to the moment of inertia (I) and angular velocity (ω) by the equation:
L=Iω
- As the skater pulls her arms inward, her moment of inertia (I) decreases because moment of inertia is proportional to the square of the radius (r) of the arms from the axis of rotation.
- Since L is constant and I decreases, it follows that ω must increase to keep the product Iω constant.
- Conclusion: ω increases
3. Kinetic Energy Calculation:
- The kinetic energy (E_k) of the skater is given by:
Ek=12Iω2
- We can also express ω in terms of L:
ω=LI
- Substituting this into the kinetic energy formula gives:
Ek=12I(LI)2=L22I
- Since L is constant and I decreases as the skater pulls her arms in, the kinetic energy Ek will increase because it is inversely proportional to I.
- Conclusion: Ek increases
Summary of Conclusions:
- Angular Momentum (L): Constant
- Angular Velocity (ω): Increases
- Kinetic Energy (E_k): Increases
True Statements:
- The true statements regarding the skater's motion are:
- A) Angular momentum (L) is constant.
- B) Angular velocity (ω) increases.
- C) Kinetic energy (E_k) increases.
- The skater is rotating about a vertical axis and pulls her arms inward. Since we are ignoring all frictional effects, there are no external torques acting on the skater. Therefore, the angular momentum (L) of the system is conserved.
- Conclusion: L=constant
- The angular momentum (L) is related to the moment of inertia (I) and angular velocity (ω) by the equation:
L=Iω
- As the skater pulls her arms inward, her moment of inertia (I) decreases because moment of inertia is proportional to the square of the radius (r) of the arms from the axis of rotation.
- Since L is constant and I decreases, it follows that ω must increase to keep the product Iω constant.
- Conclusion: ω increases
- The kinetic energy (E_k) of the skater is given by:
Ek=12Iω2
- We can also express ω in terms of L:
ω=LI
- Substituting this into the kinetic energy formula gives:
Ek=12I(LI)2=L22I
- Since L is constant and I decreases as the skater pulls her arms in, the kinetic energy Ek will increase because it is inversely proportional to I.
- Conclusion: Ek increases
- Angular Momentum (L): Constant
- Angular Velocity (ω): Increases
- Kinetic Energy (E_k): Increases
- The true statements regarding the skater's motion are:
- A) Angular momentum (L) is constant.
- B) Angular velocity (ω) increases.
- C) Kinetic energy (E_k) increases.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct142videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
Which of the following statements about kinetic energy (K.E.) is true?
View SolutionA particle with the position vector r has linear momentum p. Which of the following statements is true is respect of its angular momentum L about the origin ?
View SolutionA sphere rolling on a horizontal rough surface Collides elastically with a smooth vertical wall, as shown in Fig. State which of the following statements is true or false.
 a. After collision, the velocity of the centre of mass gets reversed.
a. After collision, the velocity of the centre of mass gets reversed.
b. Angular momentum of the sphere about the point of contact with the wall is conserved.
c. Angular momentum of the sphere about a stationary point on the horizontal surface is conserved.
d. Just after collision the point of contact with the horizontal surface is moving towards the wall.
e. After collision the friction force acts on the sphere such that it decreases the linear speed and increases the angular speed.
f. Finally, when the sphere starts rolling, it is moving away from the wall.View SolutionA sphere moving with a velocity v0 on a smooth surface suddenly enters on a rough horizontal surface as shown in Fig. State which of the following statements are true or false
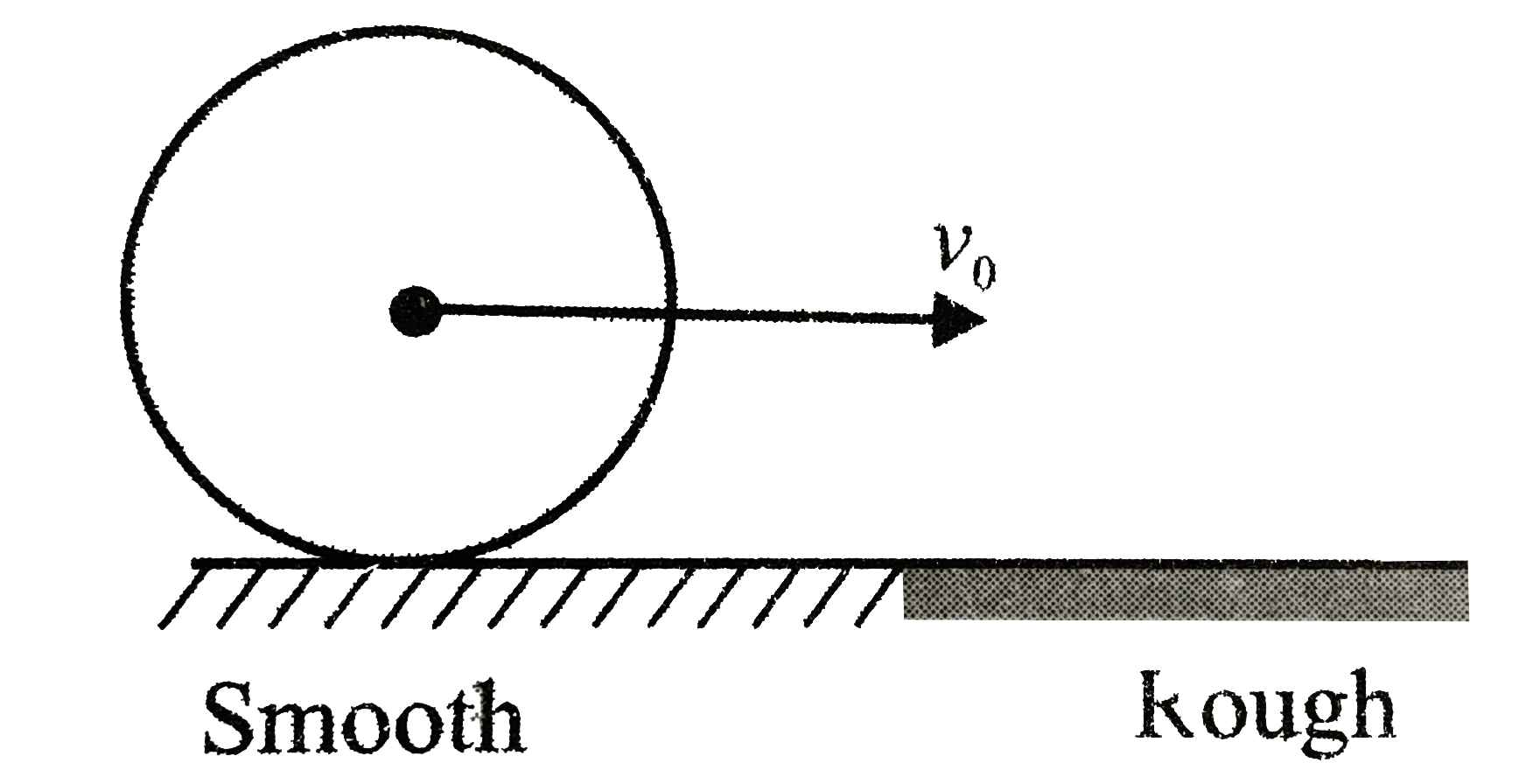
a. The sphere loses translational kinetic energy and gains rotational kinetic energy.
b. The total energy of the sphere is conserved.
c. The angular momentum of the sphere about any point OD the surface is conserved.
d. The final velocity attained by the centre of mass is 2v0/3.View SolutionA horizonral circular plate is rotating about a vertical axis passing through its centre with an angular velocity ω0. A man sitting at the centre having two blocks in his hands stretches out his hands so that the moment of inertia of the system doubles. If the kinetic energy of the system is K intially, its final kinetic energy will be
View SolutionAn ice skater having moment of inertia l rotating with angular speed ω suddenly opens her arms, which reduces her angular velocity to ω4. Calculate the change in moment of inertia of the dancer.
View SolutionAn ice skater having moment of inertia l rotating with angular speed ω suddenly opens her arms, which reduces her angular velocity to ω4. Calculate the change in moment of inertia of the dancer.
View SolutionA hollow sphere and a solid sphere of the same dimensions rotate about the same axis with the same angular velocity. Which has greater kinetic energy ?
View SolutionAn ice skater spins at 3π rad s−1 with hers arms extended. If her moment of inertia with arms folded is 75% of that with arms extended, her angular velocity when she fold her arms is
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
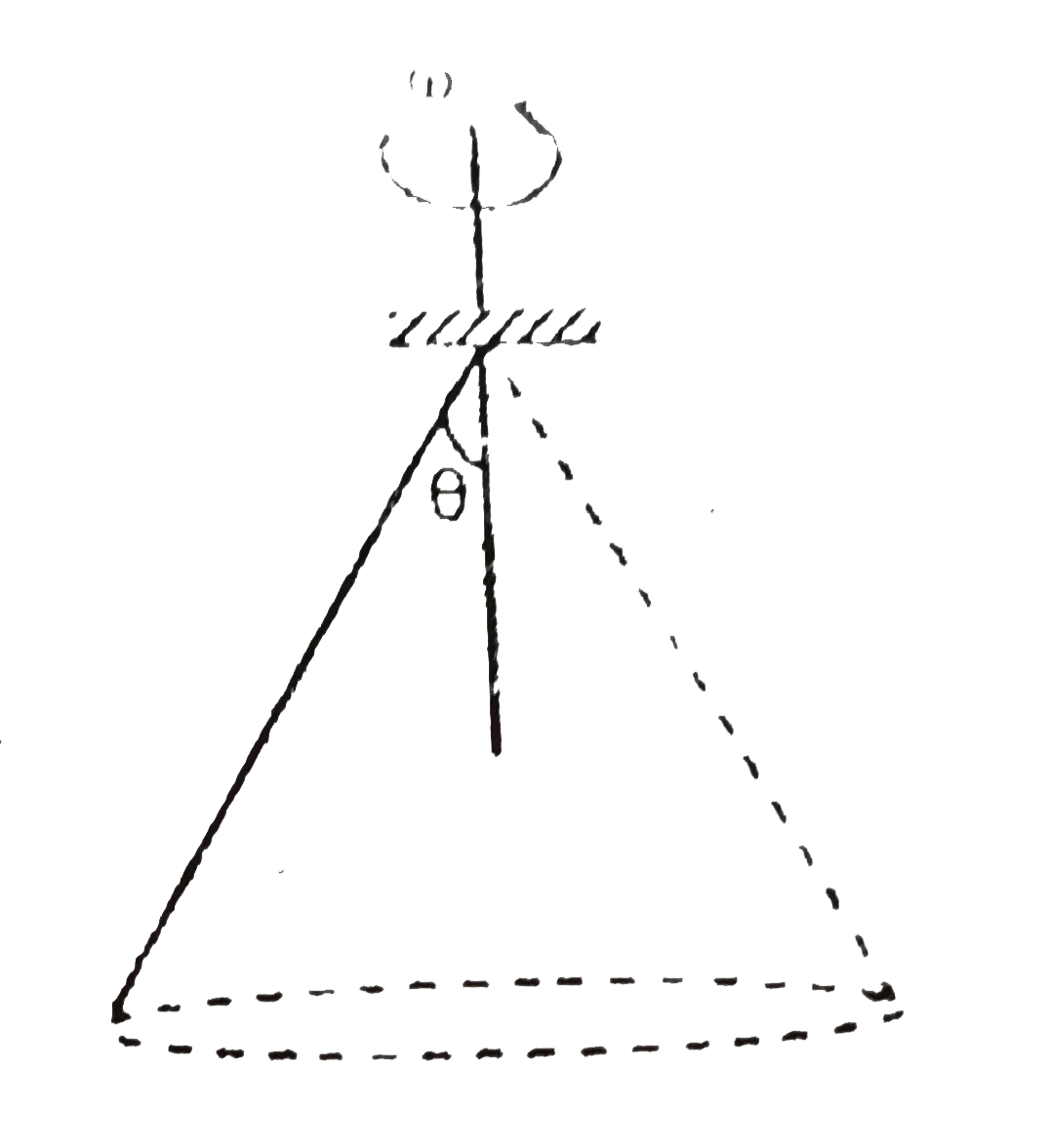 View Solution
View Solution
