A small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
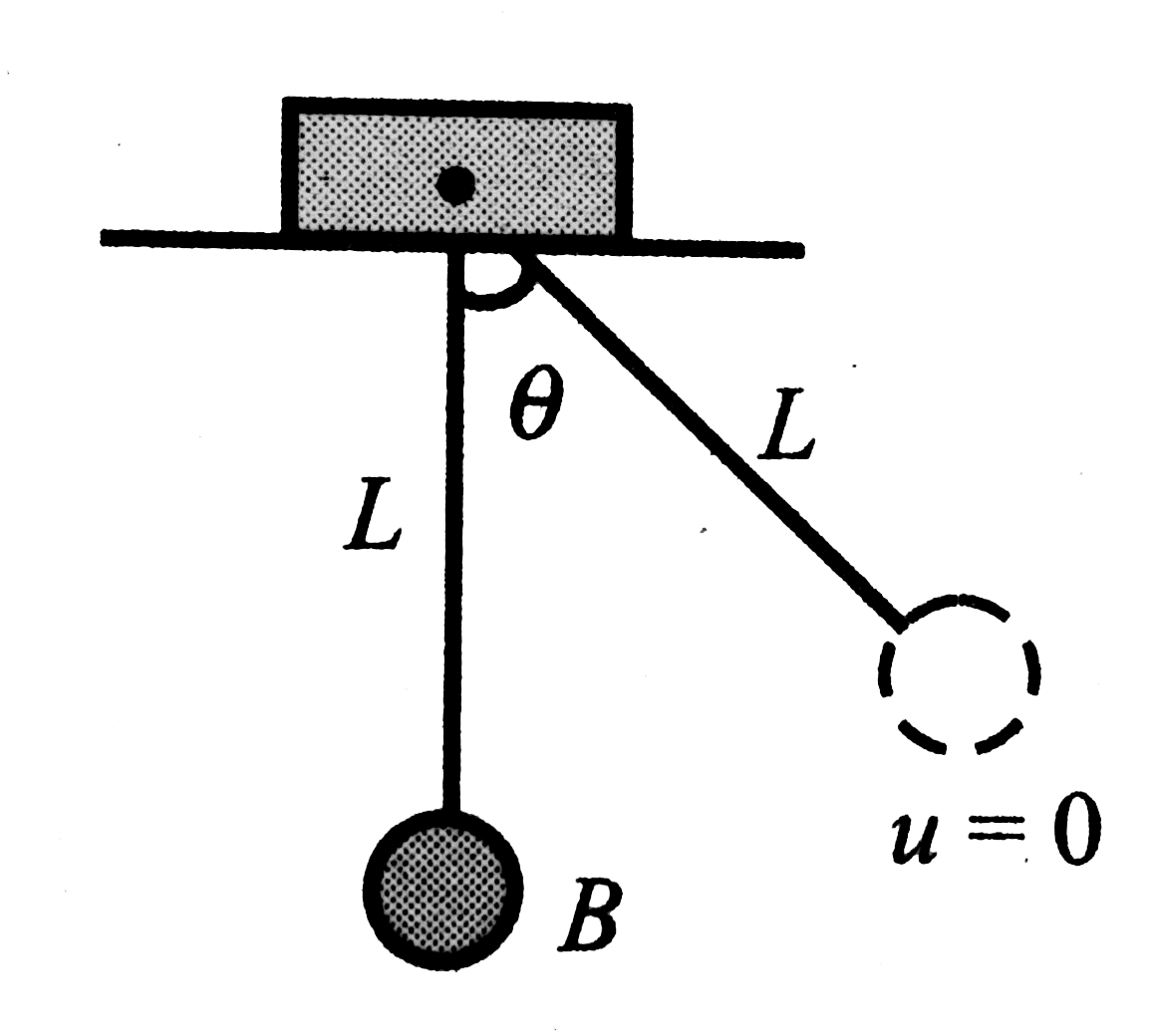 The displacement of centre of mass of A+B system till the string becomes vertical is
The displacement of centre of mass of A+B system till the string becomes vertical is
zero
L(1−cosθ)
L2(1−cosθ)
none of these
The correct Answer is:C
ycm=m1y1+m2y2m1+m2
∴△ycm=m1△y1+m2△y2m1+m2
△ycm=0−mL(1−cosθ)m+m
∴△ycm=L2(1−cosθ) in downward direction.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionA bob of mass m is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle θ in equilibrium position.
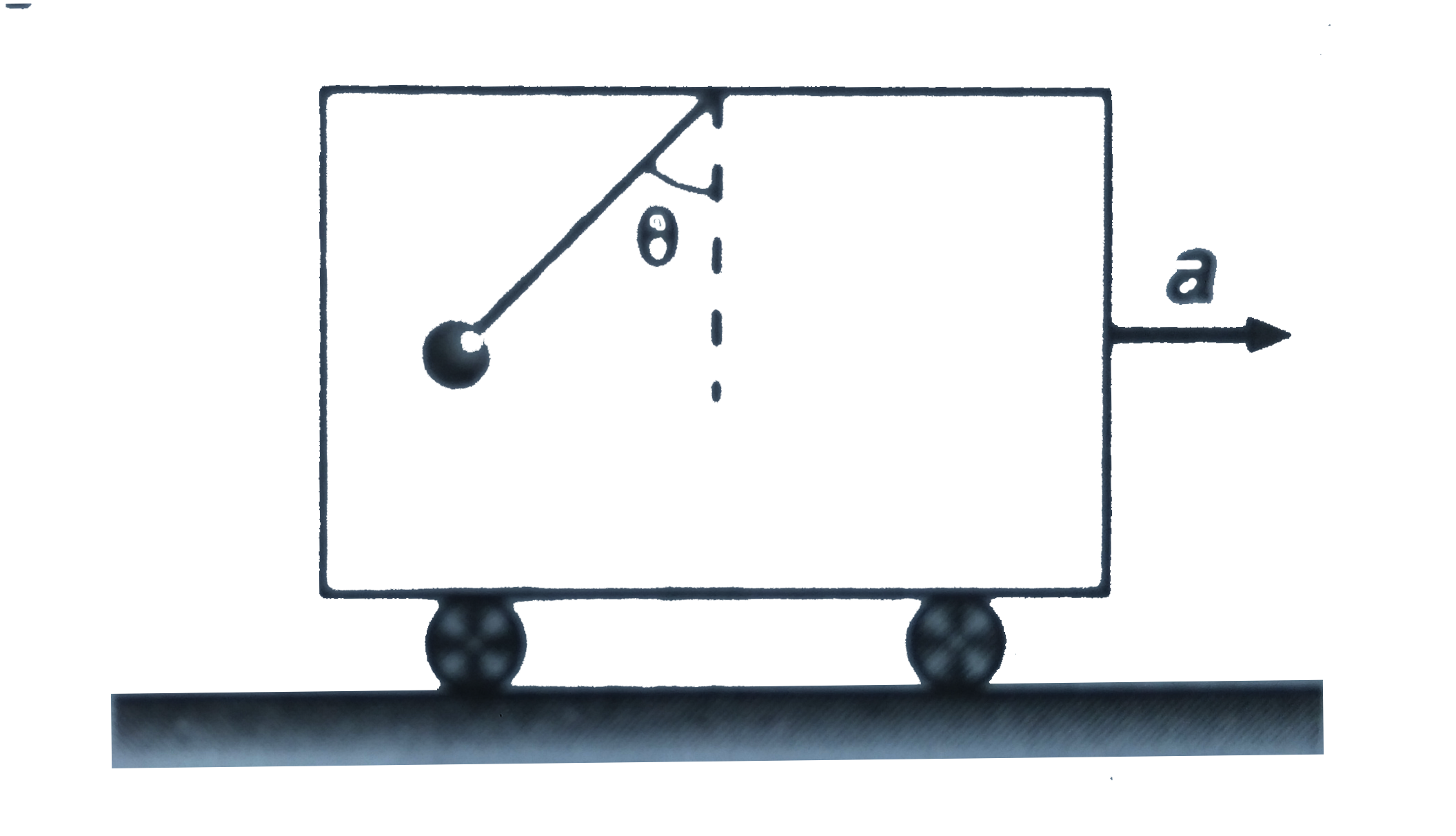
View Solution
Knowledge Check
A small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.

The displacement of block when equilibrium position isALsinθ2BLsinθCLDnone of theseA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
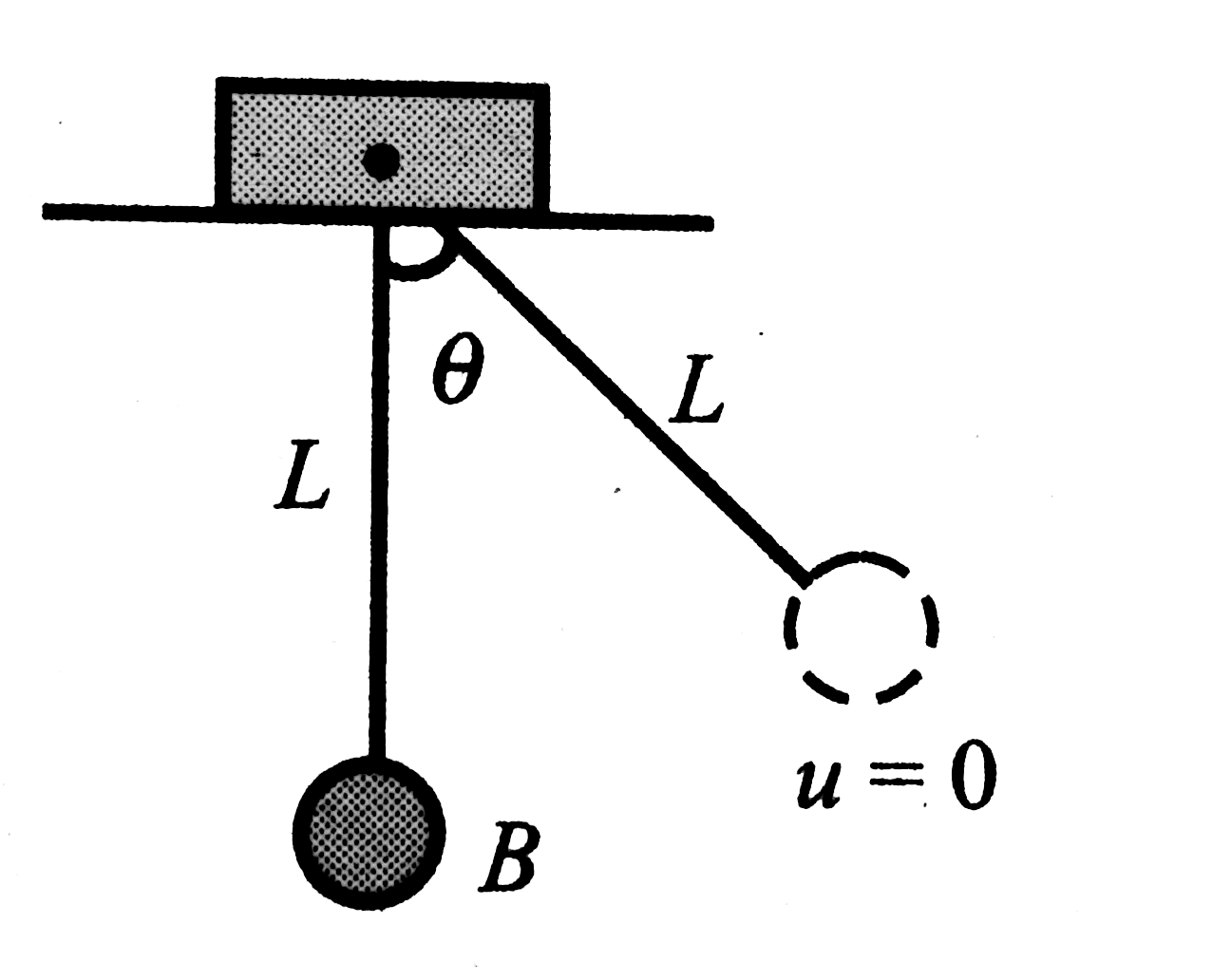
Tension in string when it is vertical, isAmgBmg(2−cosθ)Cmg(3−2cosθ)Dnone of theseA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
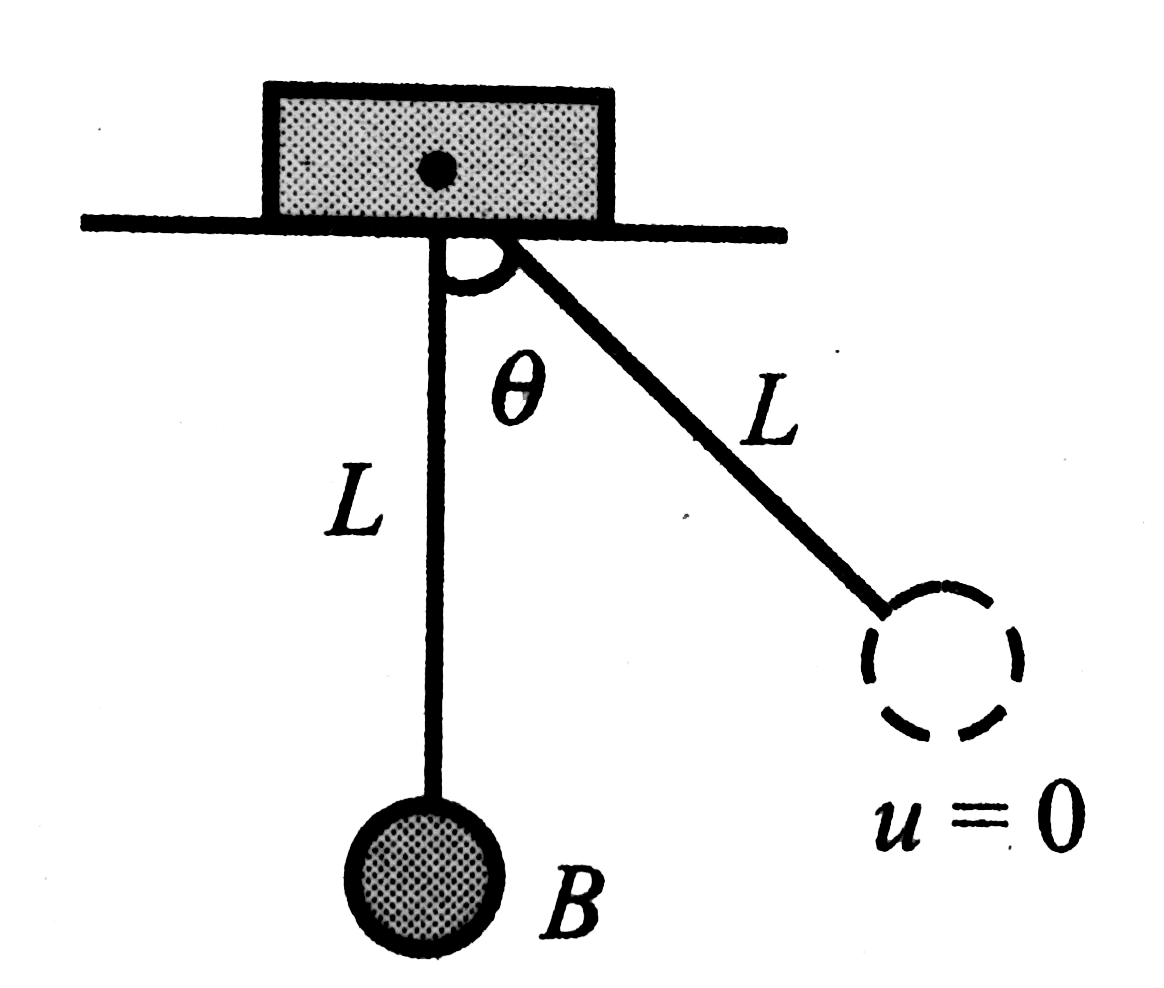
Maximum velocity of block during subsequent motion of the system after release of ball isA[gl(1−cosθ)]12B[2gl(1−cosθ)]12C[glcosθ]12Dinformation are sufficient to decide
Two identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. If the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
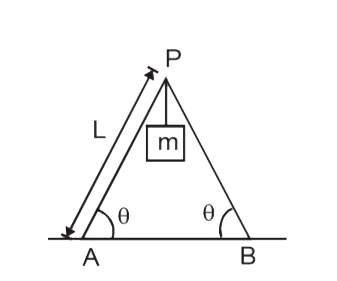
View SolutionTwo identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. if the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
View SolutionA small ring of mass m1 is connected by a string of length l to a small heavy bob of mass m2. The ring os free to move (slide) along a fixed smooth horizontal wire. The bob is given a small displacement from its equilibrium position at right angles to string. Find period of small oscillations.
_E01_106_Q01.png)
View SolutionA thin rod of mass M and length L is released from rest in position shown. The path of centre of mass of rod till the rod become horizontal is [ Assume surface is smooth]
_PHY_208_Q01.png)
View SolutionFour blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.

View Solution
