A horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
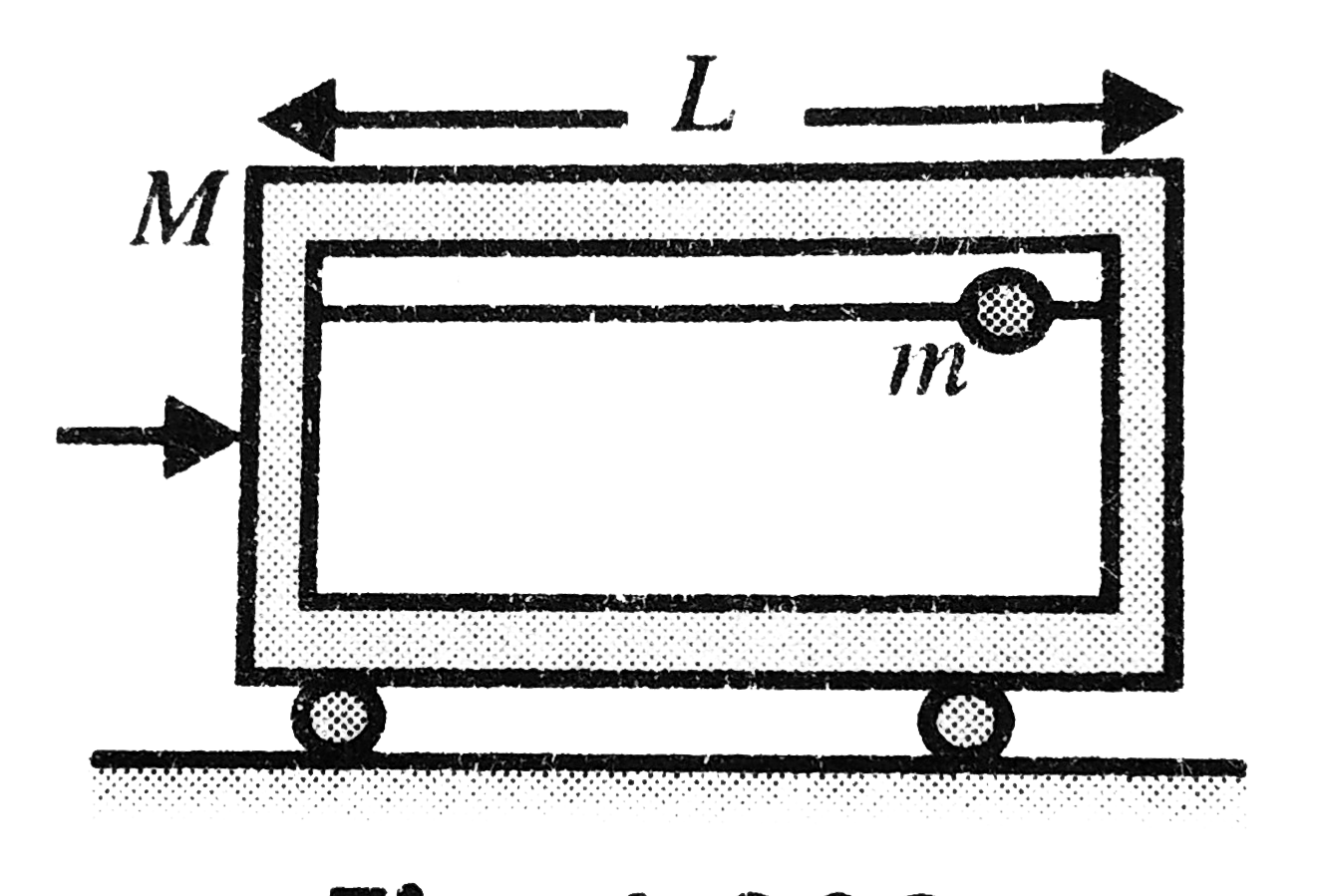
The first collision takes place at time ti and the second collision takes place at time t2. Find t2−t1
2Lv0
Lv0
L2v0
L3v0
The correct Answer is:B

Mv0=Mv1+mv2…………i
v2−v1v0=………..ii
Solve to get v1=M−mM+mv0
v2=2Mm+Mv0
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Integer16videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
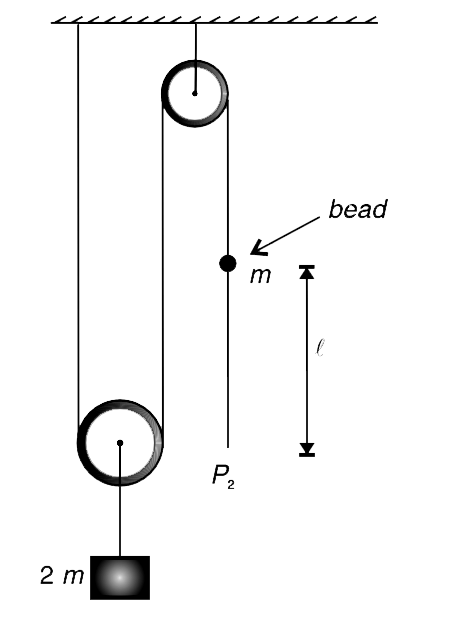
In the system shown in the fig., the bead of mass m can slide on the string. There is friction between the bead and the string. Block has mass equal to twice that of the bead. The system is released from rest with length l of the string hanging below the bead. Calculate the distance moved by the block before the bead slips out of the thread. Assume the string and pulley to be massless.
 View Solution
View Solution
A frictionless wire is fixed between A and B inside a circle of radius R. A small bead slips along the wire. Find the time taken by the bead to slip from A to B.View Solution
Knowledge Check
- Question 1 - Select One
A horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
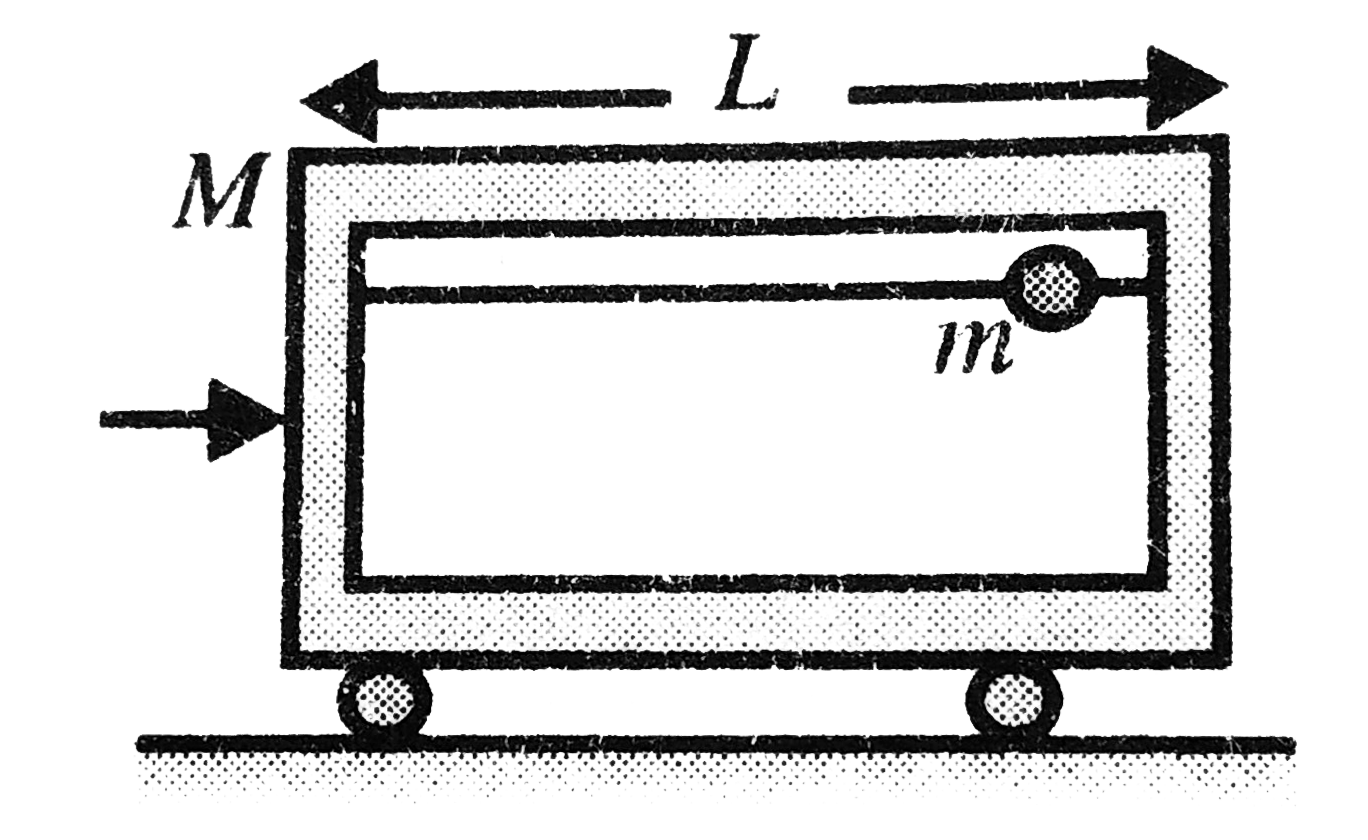
Velocity of bead just after the first collision isA−mv0m+MBMv0m+MCM−mM+mv0D2Mm+Mv0 - Question 2 - Select One
A horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
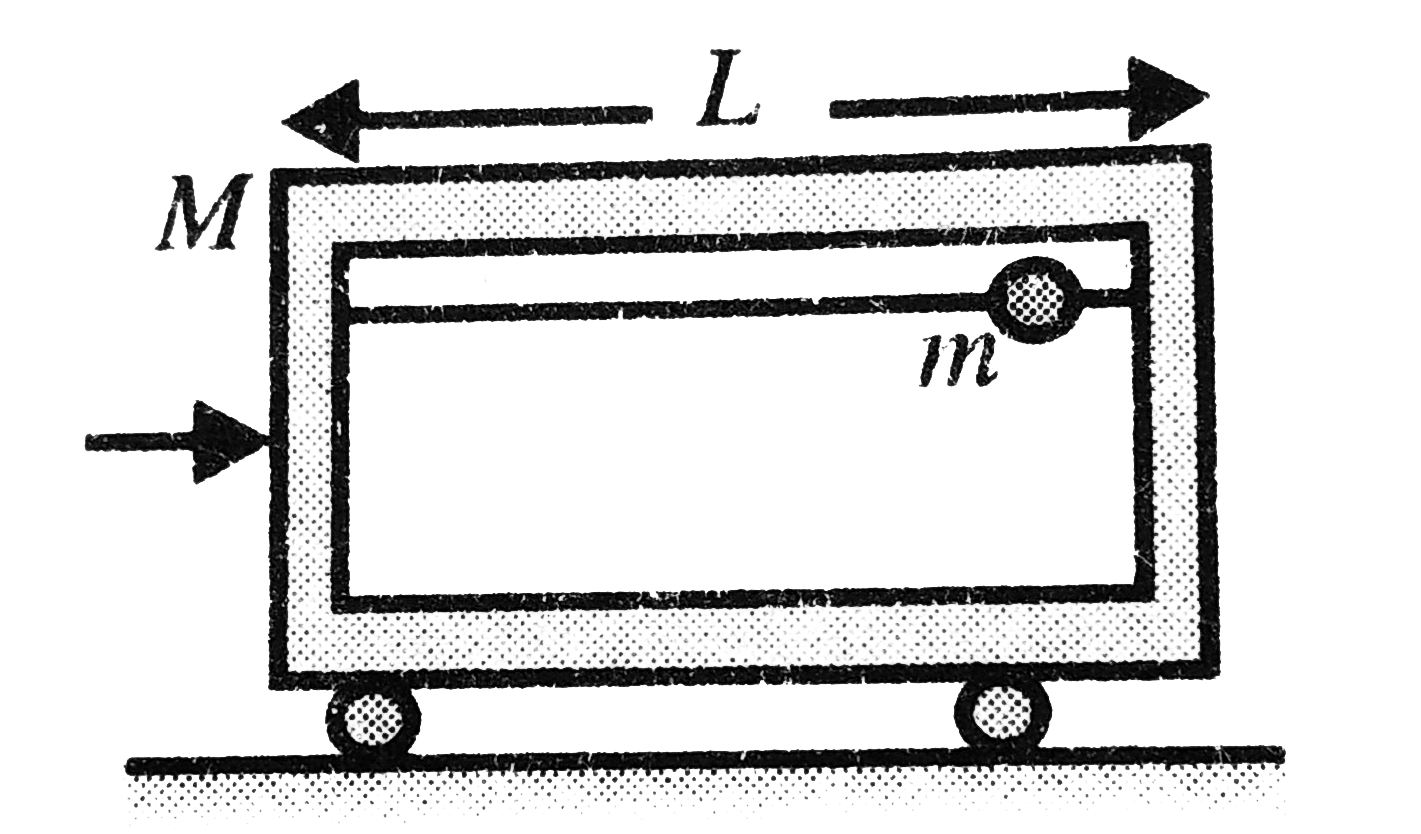
What is the velocity of the cart just after the first collision?A−mv0m+MBMv0m+MCM−mM+mv0D2Mm+Mv0 - Question 3 - Select One
A bead of mass m and diameter d is sliding back and forth with velocity v on a wire held between two right walls of length L. Assume that th ecollisions with the wall are perfectly elastic and ther is no friction. The average force that the bouncing bead exerts on the one of the walls is :_
Amv2L−dBmv2L+dC2mv2L−dD2mv2L+d
A bead of mass m moves on a rod without friction. Initially the bead is at the middle of the rod and the rod moves translationally in a vertical plane with an acceleration a0 in a direction forming angle θ with the horizontal as shown in the given figure. The acceleration of bead with respect to rod is
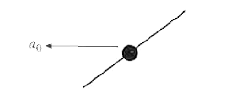 View Solution
View SolutionA bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
zView SolutionFour beads each of mass m are glued at the top, bottom and the ends of the horizontal diameter of a ring of massm. If the ring rolls without sliding with the velocity v of its, the kinetic energy of the system (beads+ring) is
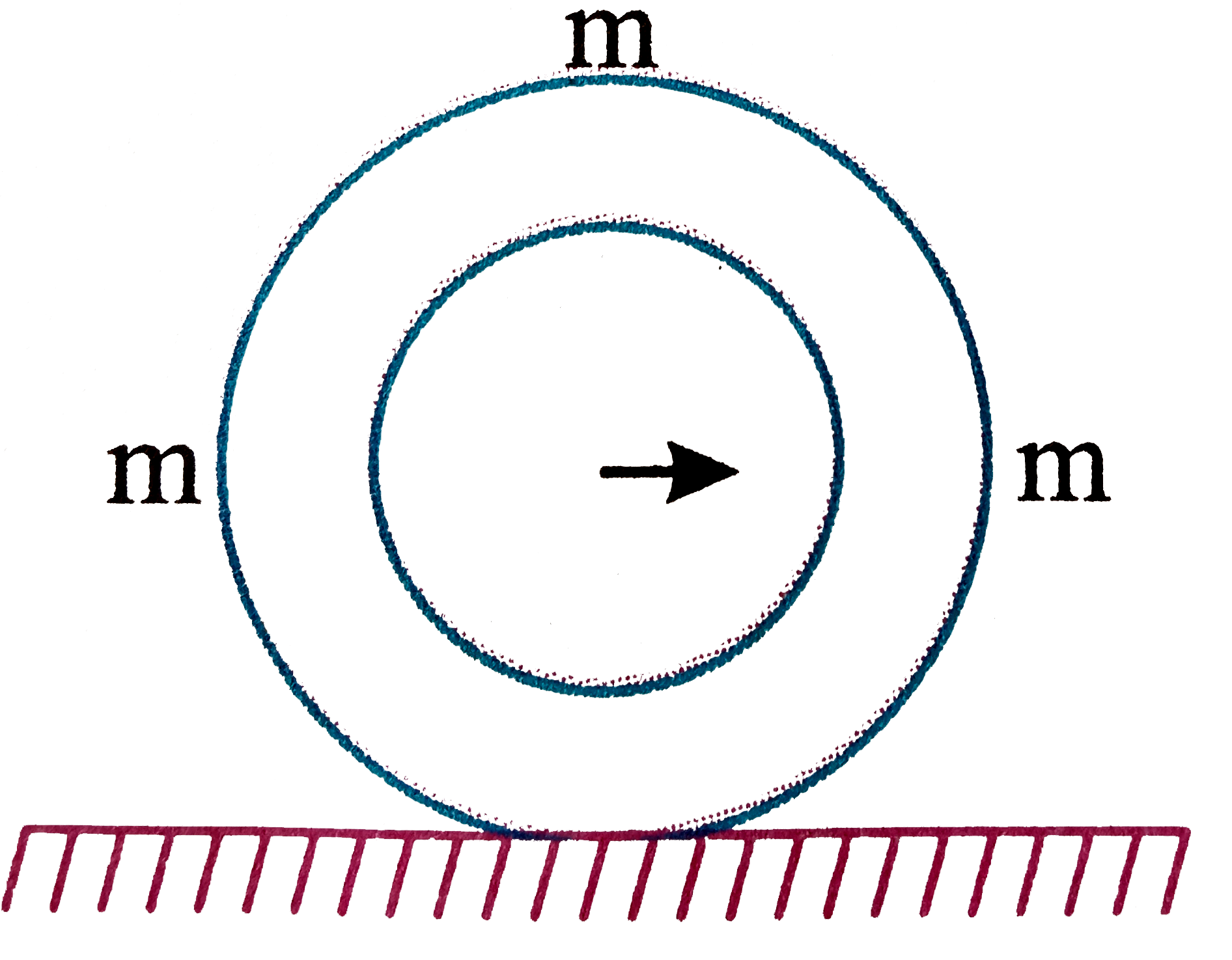 View Solution
View SolutionA ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
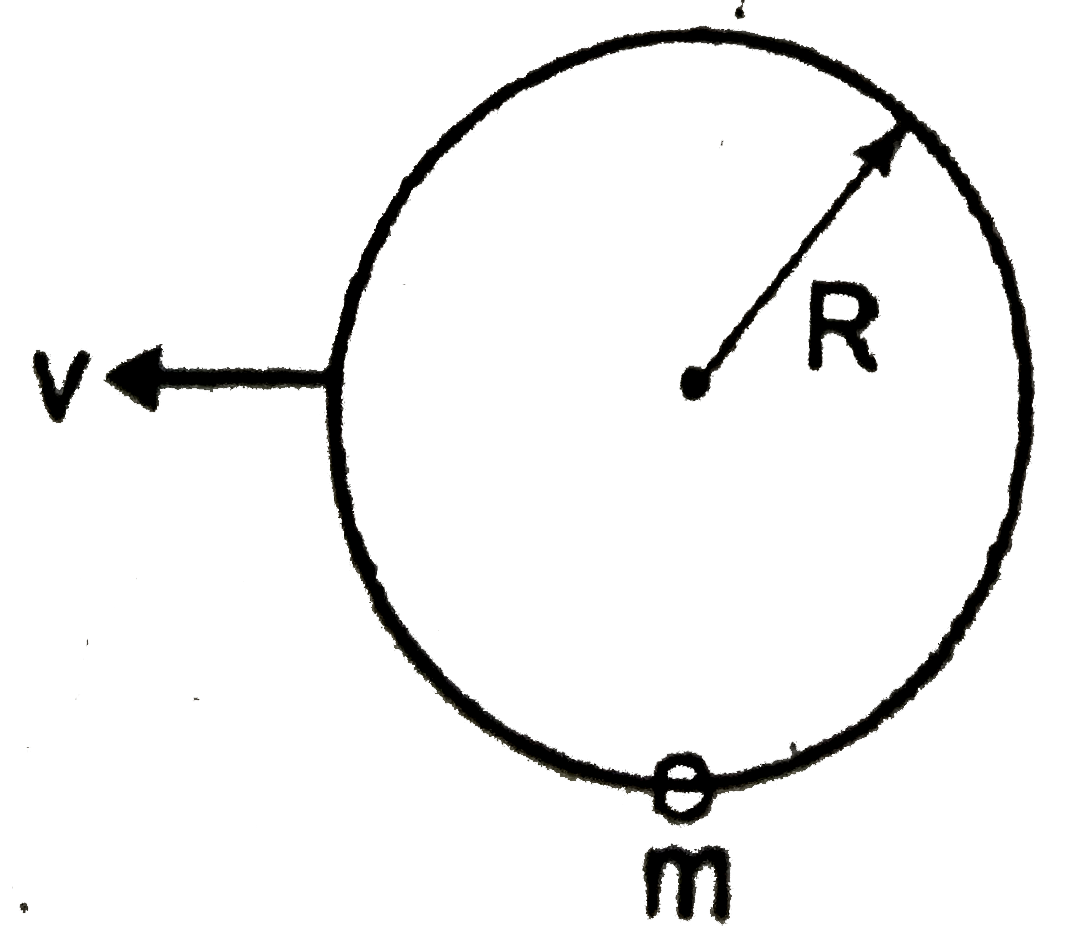 View Solution
View SolutionAn isolated smooth ring of mass M = 2m with two small beads each of mass m is as shown in the figure. Initially both the beads are at diametrically opposite points and have velocity v0 (for each) in same direction. The speed of the beads just before they collide for the first time is (complete system is placed on a smooth horizontal surface and assume each point of ring is touching the surface)
 View Solution
View Solution

