A small ball (mass m) falling under gravity in a viscous medium experi

A small steel ball of mass $m$ and radius $r$ is falling under gravity through a viscous liquid of coefficient of viscosity $η$ . If $g$ is the value of acceleration due to gravity. Then the terminal velocity of the ball is proportional to (ignore buoyancy)
A $\frac{m g (η)}{r}$
B $m g (η) r$
C $\frac{m g r}{η}$
D $\frac{m g}{r η}$
The displacement of a ball falling rest in a viscous medium is platted against time. Choose a possible option
A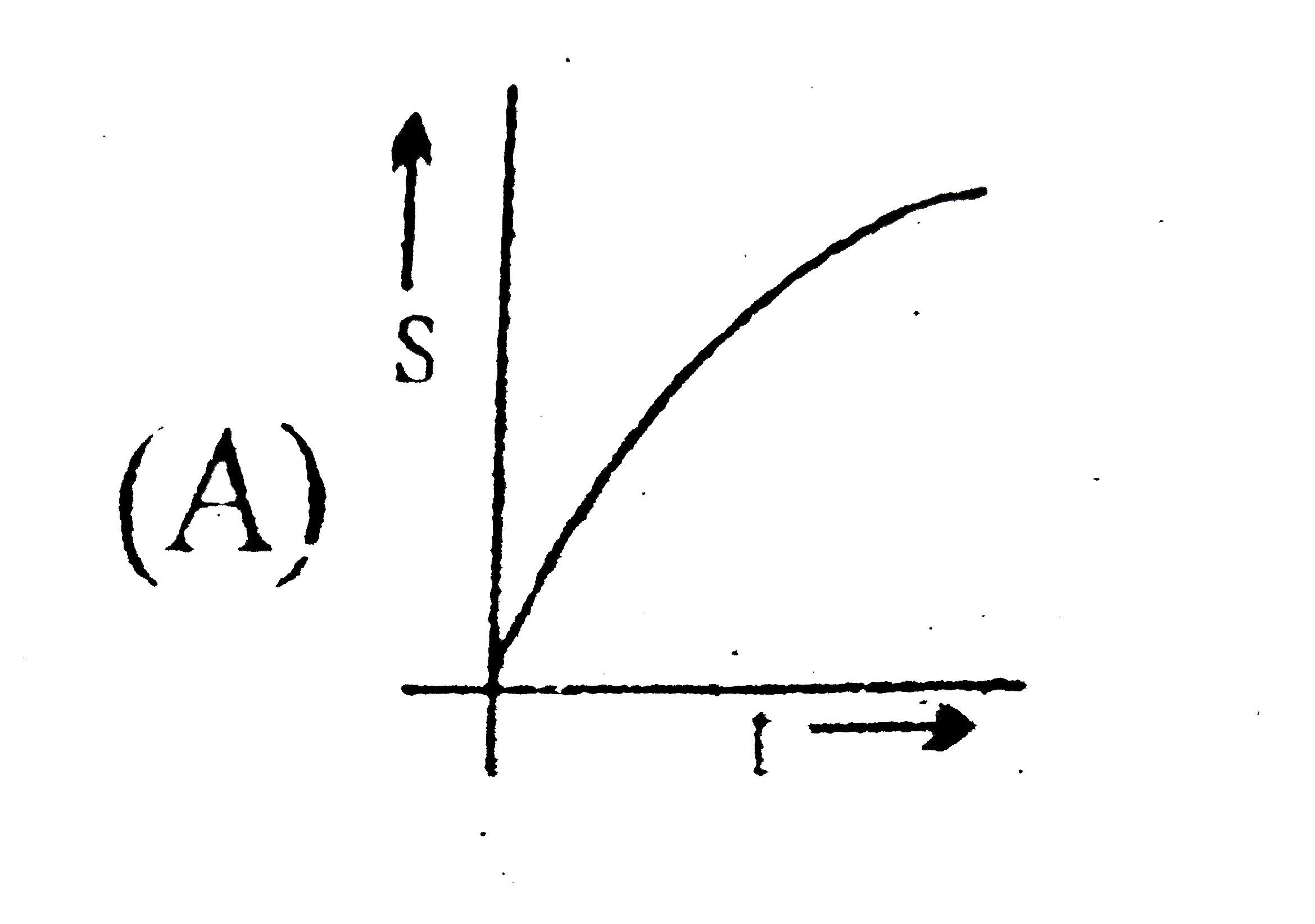
B
C
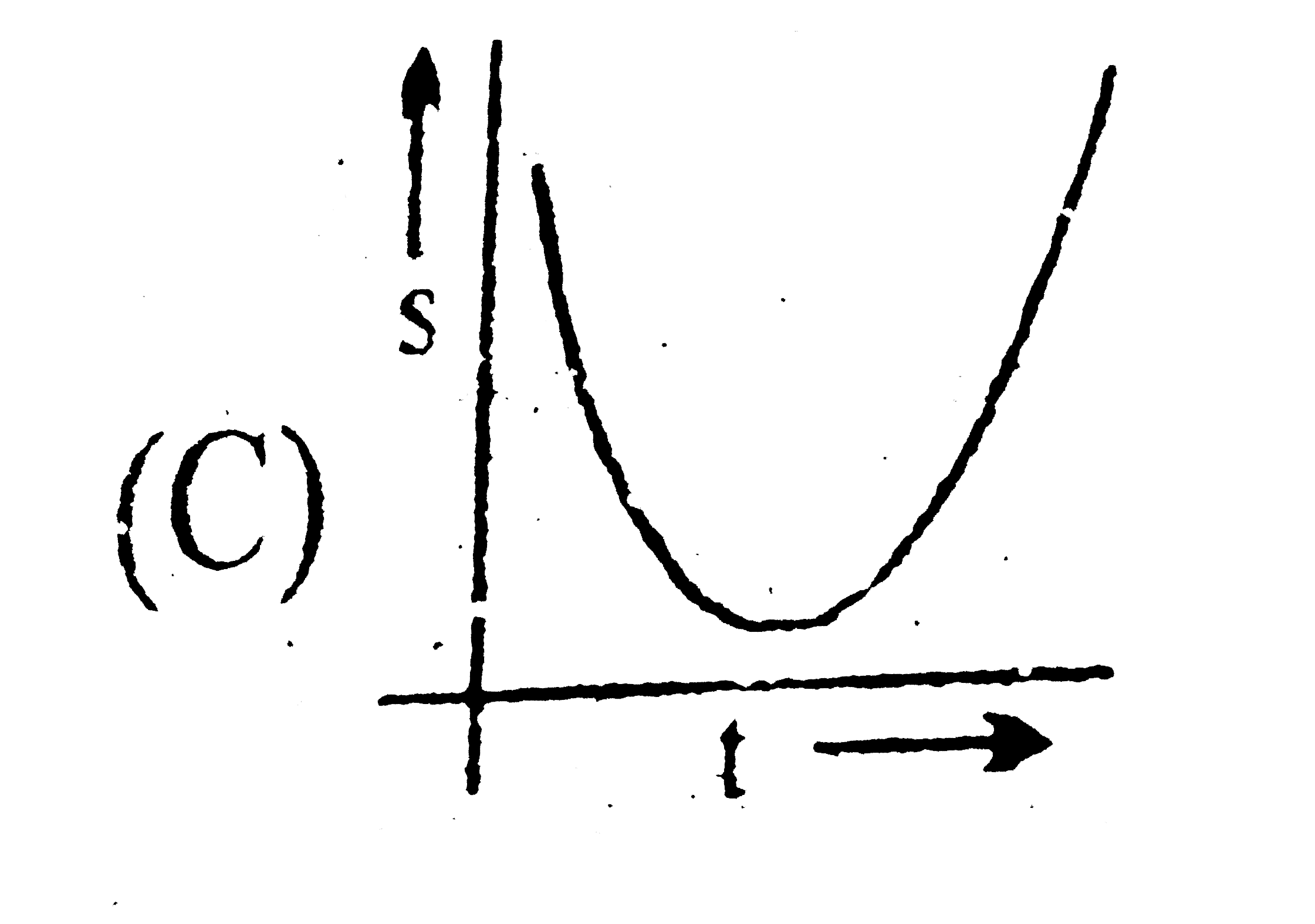D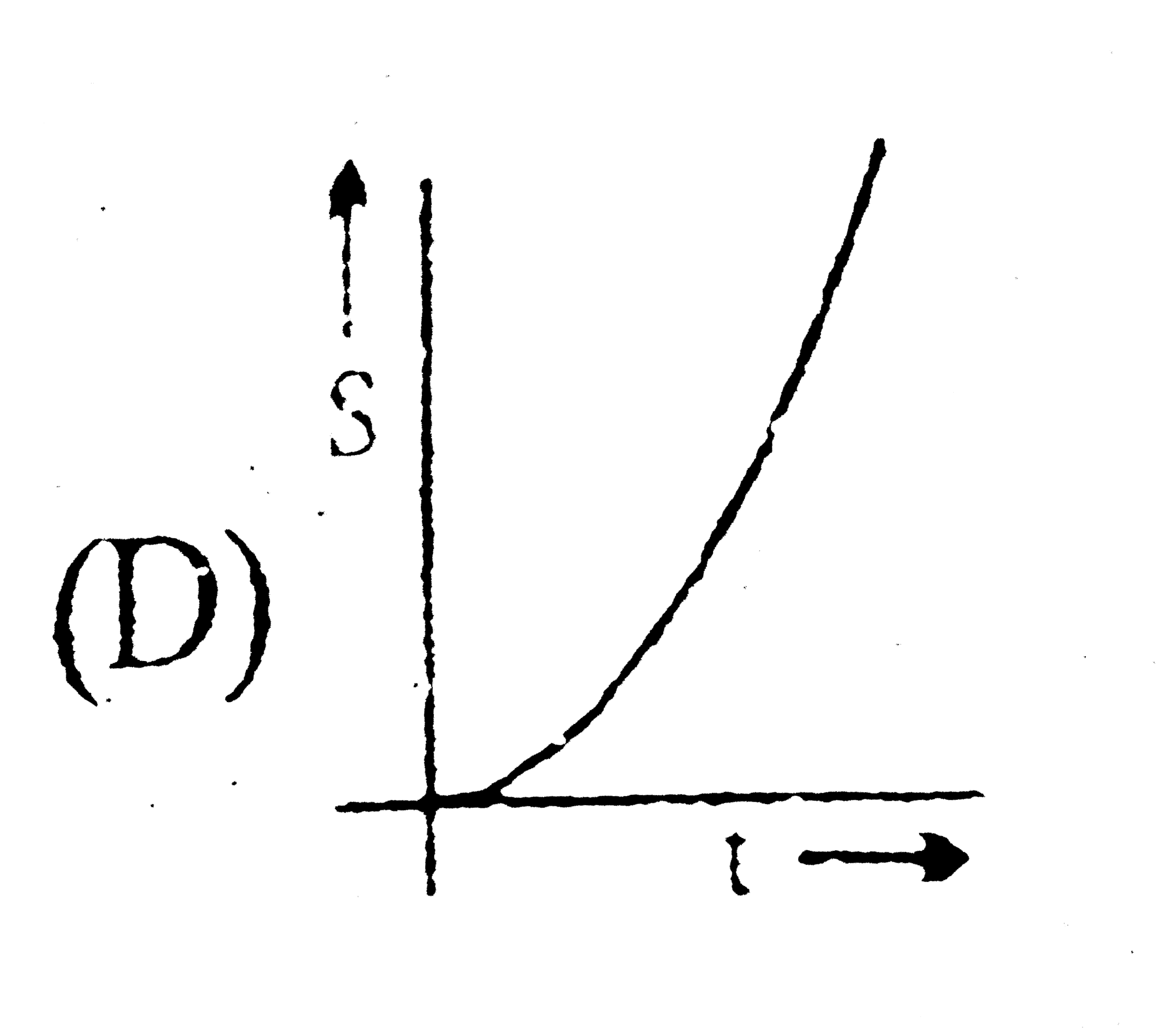
An oil drop of mass m fall through a viscous medium. The viscous drag force. $F$ is proportional to the velocity of the drop . At the instant it begins to fall the force that acts on the oil drop is (neglect buoyancy)
Amg
B $m g - F$
C $F - m g$
DF

A small ball (mass m) falling under gravity in a viscous medium experience a drag force proportional to the instantaneous speed u such that $F_{d r a g} = k u$ . Then the terminal speed of ball within viscous medium is