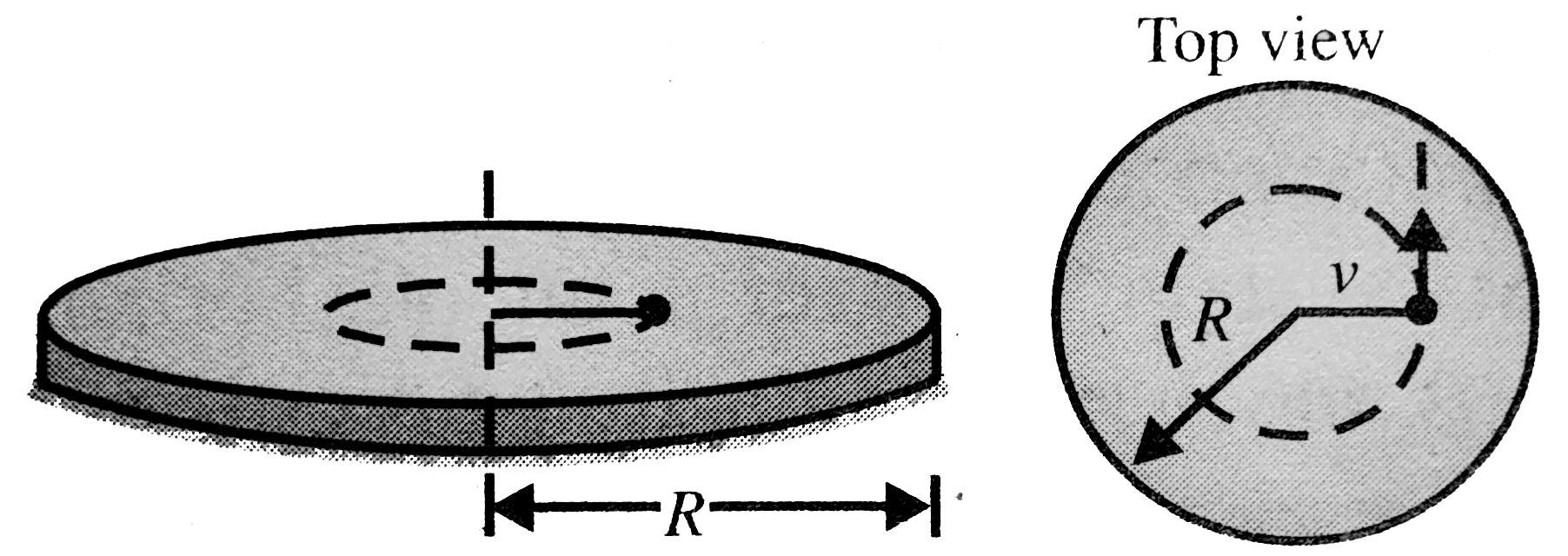
A small ball of mass 1kg is kept in circular path of radius 1m Inside a concentric smooth horizontal fixed casing of radius R. Angular speed of the ball in the circular motion is 1rads−1. At a certain moment the string, which kept the ball in the circular path breaks and the ball goes off tangentially to the wall of rigid casing and bounces off elastically and again hits the casing and bounces off. This way, the ball traces a regular hexagon. Consider all the collisions to be elastic.
Following quantities of the ball will remain a constant before and after any collision
linear momentum
kinetic energy, angular momentum about the centre of the circle
velocity, angular momentum about the centre of the circle, kinetic energy
none of these
The correct Answer is:B
Since an impulse acts on the ball during each collision, so linear momentum does not remain constant.
The impulsive force is directed towards the centre of hexagon, therefore the lever arm of this imupulsive force is zero.
As are result, it does not produce any torque and angular momentum remains costant. Further, kinetic energy also remains same for elastic collision.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Integer16videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Knowledge Check
- Question 1 - Select One
A small ball of mass 1kg is kept in circular path of radius 1m Inside a concentric smooth horizontal fixed casing of radius R. Angular speed of the ball in the circular motion is 1rads−1. At a certain moment the string, which kept the ball in the circular path breaks and the ball goes off tangentially to the wall of rigid casing and bounces off elastically and again hits the casing and bounces off. This way, the ball traces a regular hexagon. Consider all the collisions to be elastic.

Total time between the first collision and the seventh collision willA√43sB4√3sC3√3sDnone - Question 2 - Select One
A small ball of mass 1kg is kept in circular path of radius 1m Inside a concentric smooth horizontal fixed casing of radius R. Angular speed of the ball in the circular motion is 1rads−1. At a certain moment the string, which kept the ball in the circular path breaks and the ball goes off tangentially to the wall of rigid casing and bounces off elastically and again hits the casing and bounces off. This way, the ball traces a regular hexagon. Consider all the collisions to be elastic.

Total impulse imparted to the casing by the ball in first six collisions will beA6√3NsB3√3NsCzeroD12Ns - Question 3 - Select One
If a particle of mass 1 gm is moving along a circular path of radius 1 m with a velocity of 1 m/s, then the its angular momentum is
A1kgm2/sB10−2kgm2/sC10−2kgm2/sD10−1kgm2/s
A ball of mass 0.1kg is suspended by a string 30cm long Keeping the string always taut the ball describe a horizontal circle of radius 15cm Calculate the angular speed of the ball .
View SolutionA particle is revolving in a circular path of radius 2 m with constant angular speed 4 rad/s. The angular acceleration of particle is
View Solution
A ball of mass m and radius r rolls along a circular path of radius R its speed at the bottom (θ=0∘) of the path is v0 find the force of the path on the ball as a function of θ.View SolutionA body of mass 1kg is moving with a uniform speed of 1m/s in a circular path of radius 1m. The external force acting on the body is
View SolutionA body of mass 2 kg is rotating on a circular path of radius 0.5 m, with an angular velocity of 20 rad/s. If the radius of the path is doubled, then the new angular velocity will be
View Solution

