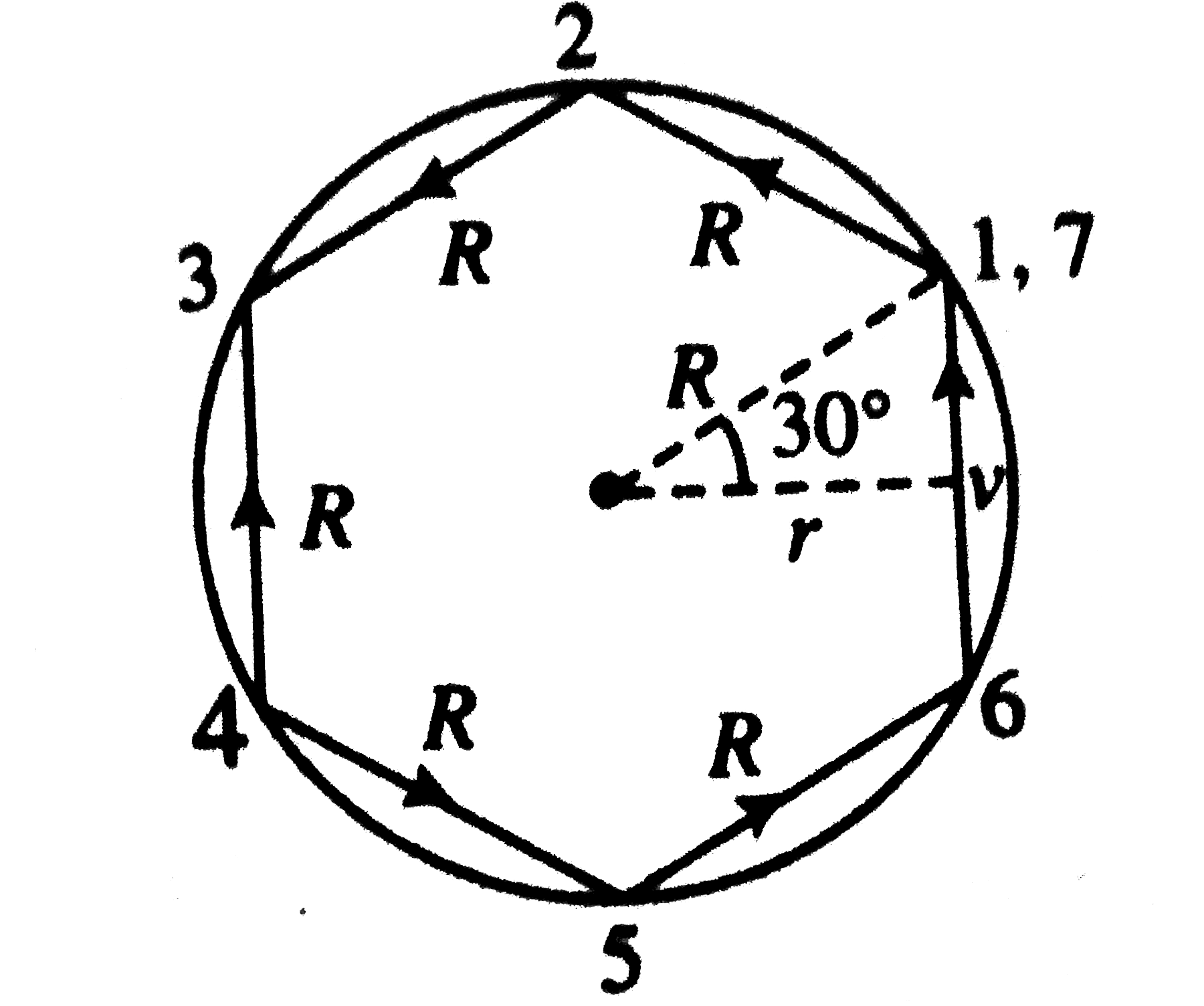
A small ball of mass $1 k g$ is kept in circular path of radius $1 m$ Inside a concentric smooth horizontal fixed casing of radius $R$ . Angular speed of the ball in the circular motion is $1 r a d s^{- 1}$ . At a certain moment the string, which kept the ball in the circular path breaks and the ball goes off tangentially to the wall of rigid casing and bounces off elastically and again hits the casing and bounces off. This way, the ball traces a regular hexagon. Consider all the collisions to be elastic.

Total time between the first collision and the seventh collision will

$\frac{\sqrt{4}}{3} s$

$4 \sqrt{3} s$

$3 \sqrt{3} s$

none

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$v = ω r$
Time between first and seventh collision.

$t = \frac{6 R}{v} = \frac{6 R}{ω r} = \frac{6 R}{ω R \cos t 30^{\circ}} = 4 \sqrt{3} s$

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A small ball of mass $1 k g$ is kept in circular path of radius $1 m$ Inside a concentric smooth horizontal fixed casing of radius $R$ . Angular speed of the ball in the circular motion is $1 r a d s^{- 1}$ . At a certain moment the string, which kept the ball in the circular path breaks and the ball goes off tangentially to the wall of rigid casing and bounces off elastically and again hits the casing and bounces off. This way, the ball traces a regular hexagon. Consider all the collisions to be elastic.

Total impulse imparted to the casing by the ball in first six collisions will be
A $6 \sqrt{3} N s$
B $3 \sqrt{3 N} s$
Czero
D $12 N s$
Question 2 - Select One
A small ball of mass $1 k g$ is kept in circular path of radius $1 m$ Inside a concentric smooth horizontal fixed casing of radius $R$ . Angular speed of the ball in the circular motion is $1 r a d s^{- 1}$ . At a certain moment the string, which kept the ball in the circular path breaks and the ball goes off tangentially to the wall of rigid casing and bounces off elastically and again hits the casing and bounces off. This way, the ball traces a regular hexagon. Consider all the collisions to be elastic.

Following quantities of the ball will remain a constant before and after any collision
Alinear momentum
Bkinetic energy, angular momentum about the centre of the circle
Cvelocity, angular momentum about the centre of the circle, kinetic energy
Dnone of these
Question 3 - Select One
If a particle of mass 1 gm is moving along a circular path of radius 1 m with a velocity of 1 m/s, then the its angular momentum is
A $1 k g m^{2} / s$
B $10^{- 2} k g m^{2} / s$
C $10^{- 2} k g m^{2} / s$
D $10^{- 1} k g m^{2} / s$