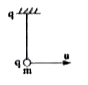
A small ball of mass 2×10−3kg, having a charge 1μC, is suspended by a string of length 0.8m. Another identical ball having the same charge is kept at the point of suspension. Determine the minimum horizontal velocity that should be imparted to the lower ball so that it can make a complete revolution.
The correct Answer is:u=√5gl−q24πε0ml=(2758)1/2m/s
To solve the problem of determining the minimum horizontal velocity that should be imparted to the lower ball so that it can make a complete revolution, we can follow these steps:
Step 1: Understand the Forces Acting on the Ball
When the lower ball is at the top of its circular path, the forces acting on it are:
- The gravitational force (downward) = mg
- The electrostatic repulsive force due to the upper ball (also downward) = kq2L2
Where:
- m=2×10−3kg (mass of the ball)
- q=1×10−6C (charge of the ball)
- L=0.8m (length of the string)
- k=9×109N m2/C2 (Coulomb's constant)
Step 2: Apply the Condition for Circular Motion
For the ball to just complete the circular motion, the centripetal force required must equal the net force acting towards the center. At the top of the circular path, the tension in the string can be considered zero for minimum velocity. Therefore, we have:
mv2L=mg+kq2L2
Where v is the velocity at the top of the circular path.
Step 3: Rearrange the Equation
Rearranging the equation gives:
v2=gL+kq2m
Step 4: Calculate the Velocity at the Top
Now substituting the values:
1. Gravitational acceleration g=10m/s2
2. m=2×10−3kg
3. q=1×10−6C
4. L=0.8m
Calculating the electrostatic force:
kq2L2=(9×109)(1×10−6)2(0.8)2=9×109×10−120.64=9×10−30.64≈0.0140625N
Now substituting into the equation for v2:
v2=(10)(0.8)+9×10−32×10−3=8+4.5=12.5
Step 5: Calculate the Minimum Velocity
Now, taking the square root to find v:
v=√12.5≈3.54m/s
Step 6: Consider Energy Conservation
To find the velocity vb at the bottom, we can use conservation of energy. The potential energy at the top will equal the kinetic energy at the bottom plus the potential energy at the bottom.
12mv2b=12mv2+mg(2L)
Substituting v2 from earlier:
v2b=v2+4gL
Substituting values:
v2b=12.5+4(10)(0.8)=12.5+32=44.5
Taking the square root gives:
vb=√44.5≈6.67m/s
Final Answer
The minimum horizontal velocity that should be imparted to the lower ball so that it can make a complete revolution is approximately 6.67 m/s.
---
When the lower ball is at the top of its circular path, the forces acting on it are:
- The gravitational force (downward) = mg
- The electrostatic repulsive force due to the upper ball (also downward) = kq2L2
- m=2×10−3kg (mass of the ball)
- q=1×10−6C (charge of the ball)
- L=0.8m (length of the string)
- k=9×109N m2/C2 (Coulomb's constant)
For the ball to just complete the circular motion, the centripetal force required must equal the net force acting towards the center. At the top of the circular path, the tension in the string can be considered zero for minimum velocity. Therefore, we have:
Rearranging the equation gives:
Now substituting the values:
2. m=2×10−3kg
3. q=1×10−6C
4. L=0.8m
Now, taking the square root to find v:
To find the velocity vb at the bottom, we can use conservation of energy. The potential energy at the top will equal the kinetic energy at the bottom plus the potential energy at the bottom.
The minimum horizontal velocity that should be imparted to the lower ball so that it can make a complete revolution is approximately 6.67 m/s.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Single Correct
56 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.3
9 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
A ball of mass m is attached to one end of a light rod of length l, the other end of which is hinged. What minimum velocity v should be imparted to the ball downwards, so that it can complete the circle ?

View SolutionThe both of a pendulum has mass m = 1 kg and charge q=40μC. Length of pendulum is = 0.9 m. The point of suspensison also has the same charge 40μC. What is the minimum speed u (in m/s) should be imparted to the bob so that it can complete vertical circle ?
View SolutionTwo charged particles having charge 2.0×10−8C. Each are joined by an isolating string of length 1m and the system is kept on a smooth horizontal task. The tension in the string.
View SolutionA ball of mass 10−2kg and having charge +3×10−6C is tied at one end of a 1m along thread. The other end of the thread is fixed and a charge −3×10−6C is placed at this end. The ball can move in the circulr orbit of radius 1m in the vertical plane. Initially, the ball is at the bottom. Find the minimum initial horizontal velocity of the ball, so that it will be able to complete the full circle.
View SolutionThree identical small balls, each of mass 0.1 g, are suspended at one point on silk thread having a length of l=20cm . What charges should be imparted to the balls for each thread to form an angle of α=30∘ with the vertical?
View SolutionIn all the four situations depicted in Column-I, a ball of mass m is connected to a string. In each case, find the tension in the string and match the appropriate entries in Column-II.
(A)(##VMCPHYXIWORBOK01_C04E03050_Q01##)Conical pendulum(P)T=mgcosθ(B)(##VMCPHYXIWORBOK01_C04E03050_Q02##)Pendulum is swinging. Angular position is the extreme position.T is tension in extreme position(Q)Tcosθ=mg(C)(##VMCPHYXIWORBOK01_C04E03050_Q03##)The car is moving with constant acceleration.The ball is at rest with respect to car(R)Speed of ball with respect to ground is constant(D)(##VMCPHYXIWORBOK01_C04E03050_Q04##)The car is moving with constant velocity. The ball is at rest with respect to car(S)Velocity of ball with respect to ground is changing continuously
View SolutionTwo charged particles having charge 2.0×10−8C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
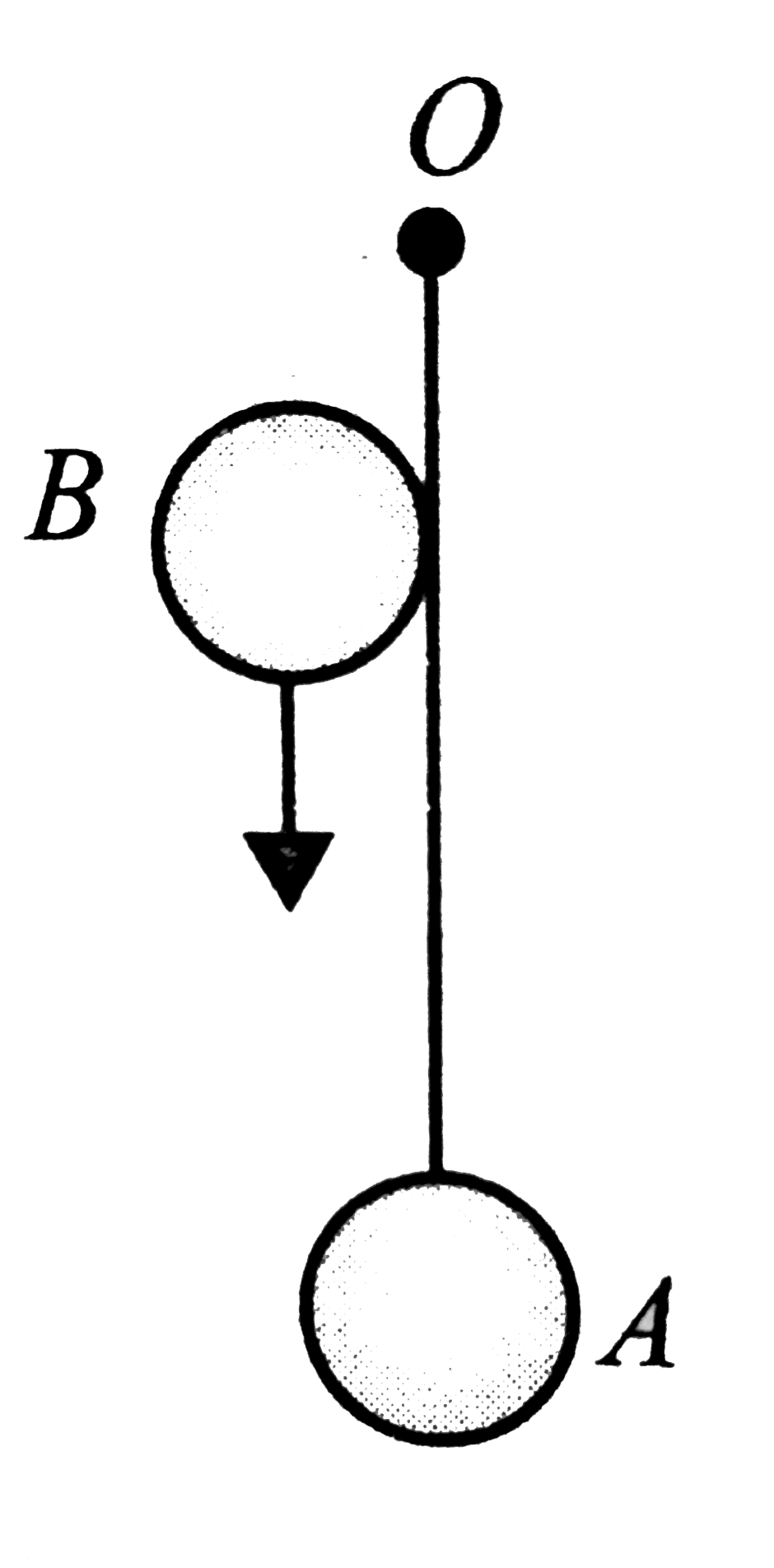
View SolutionA small steel ball A is suspended by an inextensible thread of length l=1.5m from O. Another identical ball is thrown vertically downwards such that its surface remains just in contact with thread during downward motion and collides elastically with the suspended ball. If the suspended ball just completes vertical circle after collision, calculate the velocity (in cm/s) of the falling ball just before collision (g=10ms−2).
View SolutionTwo small spheres, each having a mass of 20 g, are suspended form a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the speration between the balls at equilibrium is found to be 4 cm . Find the charge on each sphere.
View SolutionA ball of mass 0.25 kg attached to the end of a string of length 1.96 m is moving in a horizontal circle. The string will break if the tension is more than 25 N . What is the maximum speed with which the ball can be moved
View Solution
