Two charged particles having charge 2.0×10−8C. Each are joined by an isolating string of length 1m and the system is kept on a smooth horizontal task. The tension in the string.
36×10−6N
3.6×10−6N
36×106N
3.6×106N
The correct Answer is:B
To find the tension in the string connecting two charged particles, we can follow these steps:
Step 1: Identify the given values
- Charge of each particle, q=2.0×10−8C
- Distance between the charges, r=1m
- Coulomb's constant, k=9.0×109N m2/C2
Step 2: Use Coulomb's Law to calculate the electrostatic force
Coulomb's Law states that the force F between two point charges is given by:
F=kq1q2r2
Since both charges are equal, we can substitute q1=q2=q:
F=kq2r2
Step 3: Substitute the values into the formula
Substituting the known values into the equation:
F=9.0×109(2.0×10−8)2(1)2
Step 4: Calculate (2.0×10−8)2
Calculating the square of the charge:
(2.0×10−8)2=4.0×10−16
Step 5: Substitute back into the force equation
Now substituting this value back into the force equation:
F=9.0×1094.0×10−161
Step 6: Calculate the force
Calculating the force:
F=9.0×109×4.0×10−16=3.6×10−6N
Step 7: Conclusion
The tension in the string, which is equal to the electrostatic force between the two charged particles, is:
T=3.6×10−6N
Final Answer
The tension in the string is approximately 3.6×10−6N.
---
- Charge of each particle, q=2.0×10−8C
- Distance between the charges, r=1m
- Coulomb's constant, k=9.0×109N m2/C2
Coulomb's Law states that the force F between two point charges is given by:
F=kq1q2r2
Since both charges are equal, we can substitute q1=q2=q:
F=kq2r2
Substituting the known values into the equation:
F=9.0×109(2.0×10−8)2(1)2
Calculating the square of the charge:
(2.0×10−8)2=4.0×10−16
Now substituting this value back into the force equation:
F=9.0×1094.0×10−161
Calculating the force:
F=9.0×109×4.0×10−16=3.6×10−6N
The tension in the string, which is equal to the electrostatic force between the two charged particles, is:
T=3.6×10−6N
The tension in the string is approximately 3.6×10−6N.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise
57 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise-I
80 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
Similar Questions
Two charged particles having charge 2.0×10−8C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
View Solution(i) Two charged particles having vharge 4.0×10−6C and mass 24×10−3Kg each are joining by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
(ii) If suddenly string is cut then what is the acceleration of each particle ?
(iii) Are they having equal acceleration ?
View Solution
Knowledge Check
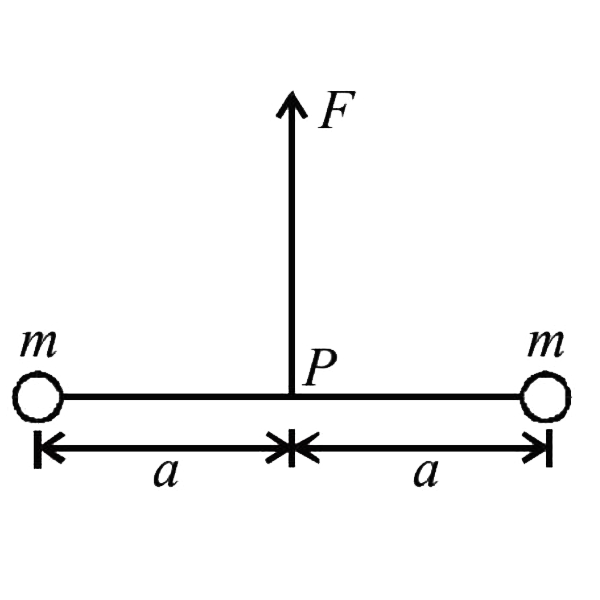
Two identical small masses each of mass m are connected by a light inextensible string on a smooth horizontal floor. A constant force F is applied at the mid point of the string as shown in fig. find the acceleration of each mass towards each other.
 AF2ma√a2−x2BF2m−x√a2−x2CF2mxaDF2m√a2−x2x
AF2ma√a2−x2BF2m−x√a2−x2CF2mxaDF2m√a2−x2x
Two charged particles, having equal charges of 2.0×10−5C each, are brought from infinity to within a separation of 10 cm. Find the increase in the electric potential energy during the process.
View SolutionTwo points charges are placed on x-axis as shown, a = 1 cm, q=1μC , mass of each particle m=6g. The charges are tied at the end of an inextensible string of length 2a. The whole system is free to move on a horizontal frictionless surface.

What is the tension in the string?
View SolutionTwo particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance a from the centre P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is
View SolutionTwo particles of masses m1andm2 are connected to a string and the system is rotated in a horizontal plane with 'P' as center. The ratio of tension in the two parts of string is

View SolutionTwo particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be

View SolutionTwo charges particles each having equal charges 2×10−5C are brought from infinity to within a separation of 10 cm. Calculate the increase in potential energy during the process and the work required for this purpose.
View SolutionTwo points charges are placed on x-axis as shown, a = 1 cm, q=1μC , mass of each particle m=6g. The charges are tied at the end of an inextensible string of length 2a. The whole system is free to move on a horizontal frictionless surface.

Now suppose a third charge of equal value +q is fixed at the point (a/2,0) and the system of charges A and B is released. There is no friction between third charge and string. Find the maximum velocity of the system of charges A and B.
View Solution
