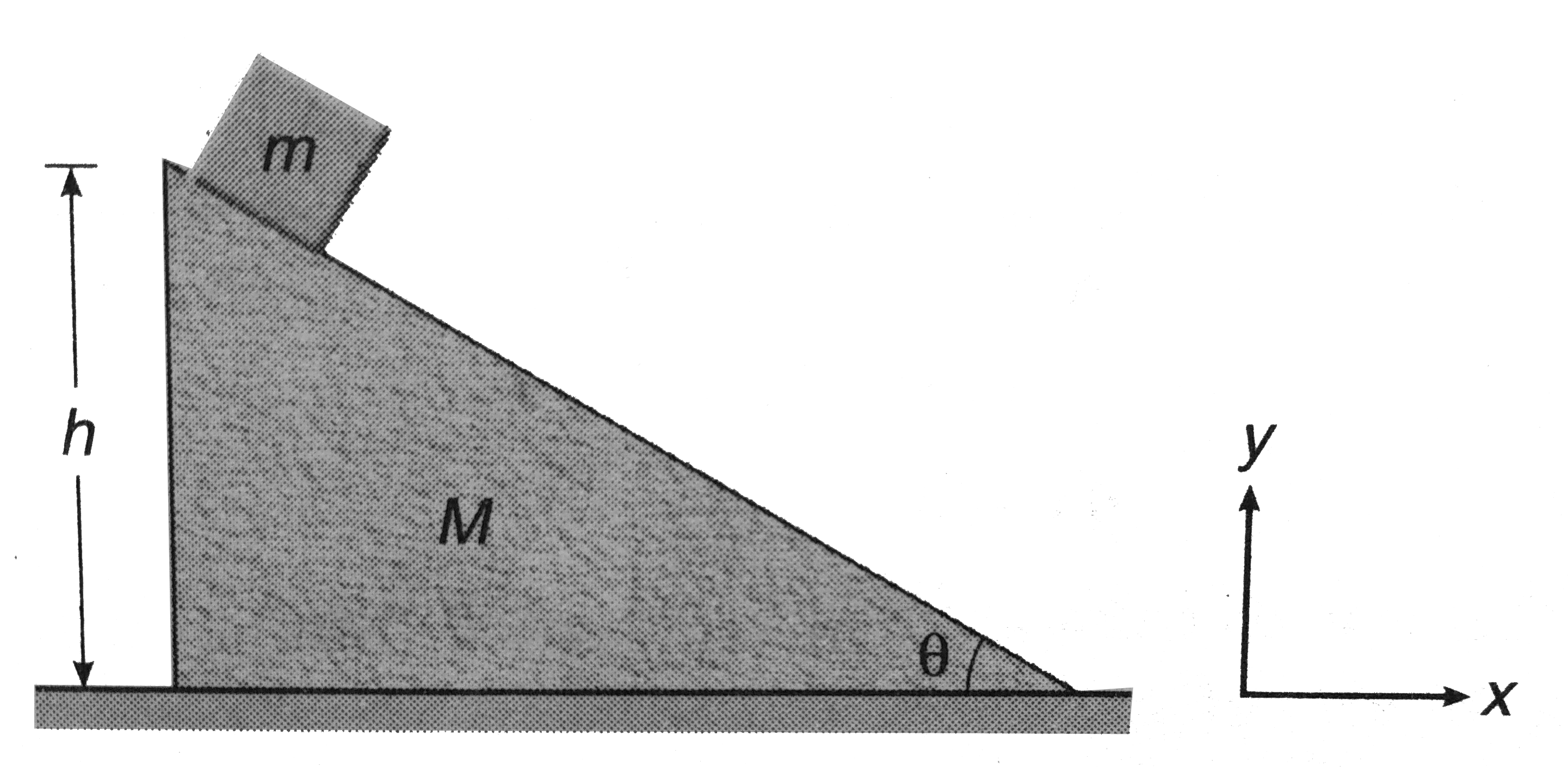
A small block of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. If h be the height of wedge and θ is the inclination, then the distance moved by the wedge as the block reaches the foot of the wedge is
(a) MhcotθM+m
(b) mhcotθM+m
(c) MhcosecθM+m
(d) mhcosecθM+m
The correct Answer is:B
To solve the problem of the small block of mass m placed on a smooth wedge of mass M, we need to analyze the motion of both the block and the wedge as the block slides down the incline of the wedge.
1. Understanding the System:
- We have a block of mass m resting on a wedge of mass M. The wedge is inclined at an angle θ and has a height h.
- Both the block and the wedge are on smooth (frictionless) surfaces.
2. Initial Setup:
- The block starts from rest at the top of the wedge.
- The wedge can slide horizontally without friction.
3. Conservation of Momentum:
- Since there are no external horizontal forces acting on the system, the horizontal momentum of the system is conserved.
- Initially, both the block and the wedge are at rest, so the total momentum is zero.
4. Analyzing Forces:
- As the block slides down the wedge, it exerts a normal force on the wedge. By Newton's third law, the wedge exerts an equal and opposite force on the block.
- The normal force can be resolved into horizontal and vertical components. The horizontal component will cause the wedge to move.
5. Calculating the Distance Moved by the Wedge:
- When the block slides down the wedge, it will move a vertical distance h downwards.
- The horizontal distance moved by the block can be calculated using trigonometry:
\(
d_{block} = h \cdot \tan(\theta)
\)
- The wedge will move a distance d∧ in the opposite direction due to conservation of momentum. Since the momentum is conserved, the horizontal distance moved by the wedge will be equal to the horizontal component of the block's movement:
\(
d_{wedge} = d_{block} \cdot \frac{m}{M}
\)
- Therefore, substituting the expression for dblock:
\(
d_{wedge} = h \cdot \tan(\theta) \cdot \frac{m}{M}
\)
6. Final Expression:
- The total distance moved by the wedge as the block reaches the foot of the wedge is:
\(
d_{wedge} = \frac{m}{M} \cdot h \cdot \tan(\theta)
\)
Final Answer:
The distance moved by the wedge as the block reaches the foot of the wedge is \( \frac{m}{M} \cdot h \cdot \tan(\theta) \).
- We have a block of mass m resting on a wedge of mass M. The wedge is inclined at an angle θ and has a height h.
- Both the block and the wedge are on smooth (frictionless) surfaces.
- The block starts from rest at the top of the wedge.
- The wedge can slide horizontally without friction.
- Since there are no external horizontal forces acting on the system, the horizontal momentum of the system is conserved.
- Initially, both the block and the wedge are at rest, so the total momentum is zero.
- As the block slides down the wedge, it exerts a normal force on the wedge. By Newton's third law, the wedge exerts an equal and opposite force on the block.
- The normal force can be resolved into horizontal and vertical components. The horizontal component will cause the wedge to move.
- When the block slides down the wedge, it will move a vertical distance h downwards.
- The horizontal distance moved by the block can be calculated using trigonometry:
\(
d_{block} = h \cdot \tan(\theta)
\)
- The wedge will move a distance d∧ in the opposite direction due to conservation of momentum. Since the momentum is conserved, the horizontal distance moved by the wedge will be equal to the horizontal component of the block's movement:
\(
d_{wedge} = d_{block} \cdot \frac{m}{M}
\)
- Therefore, substituting the expression for dblock:
\(
d_{wedge} = h \cdot \tan(\theta) \cdot \frac{m}{M}
\)
- The total distance moved by the wedge as the block reaches the foot of the wedge is:
\(
d_{wedge} = \frac{m}{M} \cdot h \cdot \tan(\theta)
\)
The distance moved by the wedge as the block reaches the foot of the wedge is \( \frac{m}{M} \cdot h \cdot \tan(\theta) \).
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective
32 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Assertion And Reason
15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest

View SolutionA block of mass m is placed on a smooth wedge of mass M, as shown in the figure . Just after placiing block m over wedge M.
View SolutionA block of mass 2kg slides down the face of a smooth 45∘ wedge of mass 9kg as shown in the figure. The wedge is placed on a frictionless horizontal surface. Determine the acceleration of the wedge.

View SolutionA block of mass m is placed at the bottom of a massless smooth wedge which if placed on a horizontal surface. When we push the wedge with a constant force, the block moves up the wedge. Find the work done by the external agent when the block has a speed v and is reaches the top of the wedge.

View SolutionA block of mass m slides over a smooth wedge of mass M which is placed over a rough horizontal surface . The centre of mass of the system will move towards left

Here μ = coefficient of friction between the wedge and the ground .
View SolutionA block of mass m is released from the top of a wedge of mass M as shown in figure. Find the displacement of wedges on the horizontal ground when the block reaches the bottom of the wedges. Neglect friction everywhere.
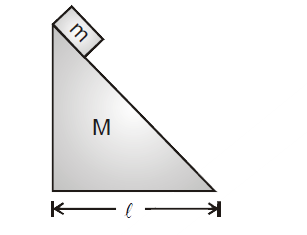
View SolutionA wedge shaped block A' of mass M is at rest on a smooth horizontal surface. A small block 'B' of mass 'm' placed at the top edge of inclined plane of length 'l' as shown in the figure. By the time, the block 'B' reaches the bottom end, the wedge A moves a distance of:

View SolutionA wedge having a vertical slot in it is placed on smooth horizontal surface as shown in the figure. Two blocks are arranged as shown in the figure. The system is released from rest calculate the speed of the wedge when block 1 comes down a distance h.

View Solution
