A small body of mass m slides without friction from the top of a hemisphere of radius r. At what height will the body be detached from the surface of hemisphere?

h=r
h=r/2
h=r/3
2r/3
The correct Answer is:C
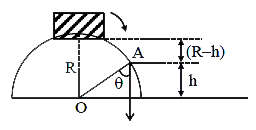
Fromfigure,
gcosθ=v2r
v2=grcosθ
cosθ=r−hr
∴ v2=gr(r−h)r=g(r−h) ....(i)
By third kinematical equation of motion
v2=2gh …(ii)
From Eqs.(i) and (ii) g(r−h)=2gh
∴ h=r3
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CIRCULAR MOTIONEXERCISE - MHT CET CORNER
21 Videos
- CIRCULAR MOTIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE 1
54 Videos
- ATOMS, MOLECULES AND NUCLEI BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - MHT CET Corner
30 Videos
- COMMUNICATION SYSTEMBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - COMMUNICATION SYSTEMEXERCISE - MHC CET Corner
6 Videos
Similar Questions
A small body of mass m slides without friction from the top of a hemisphere of radius r. At what hight will the body be detached from the centre of hemisphere?

View SolutionA small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
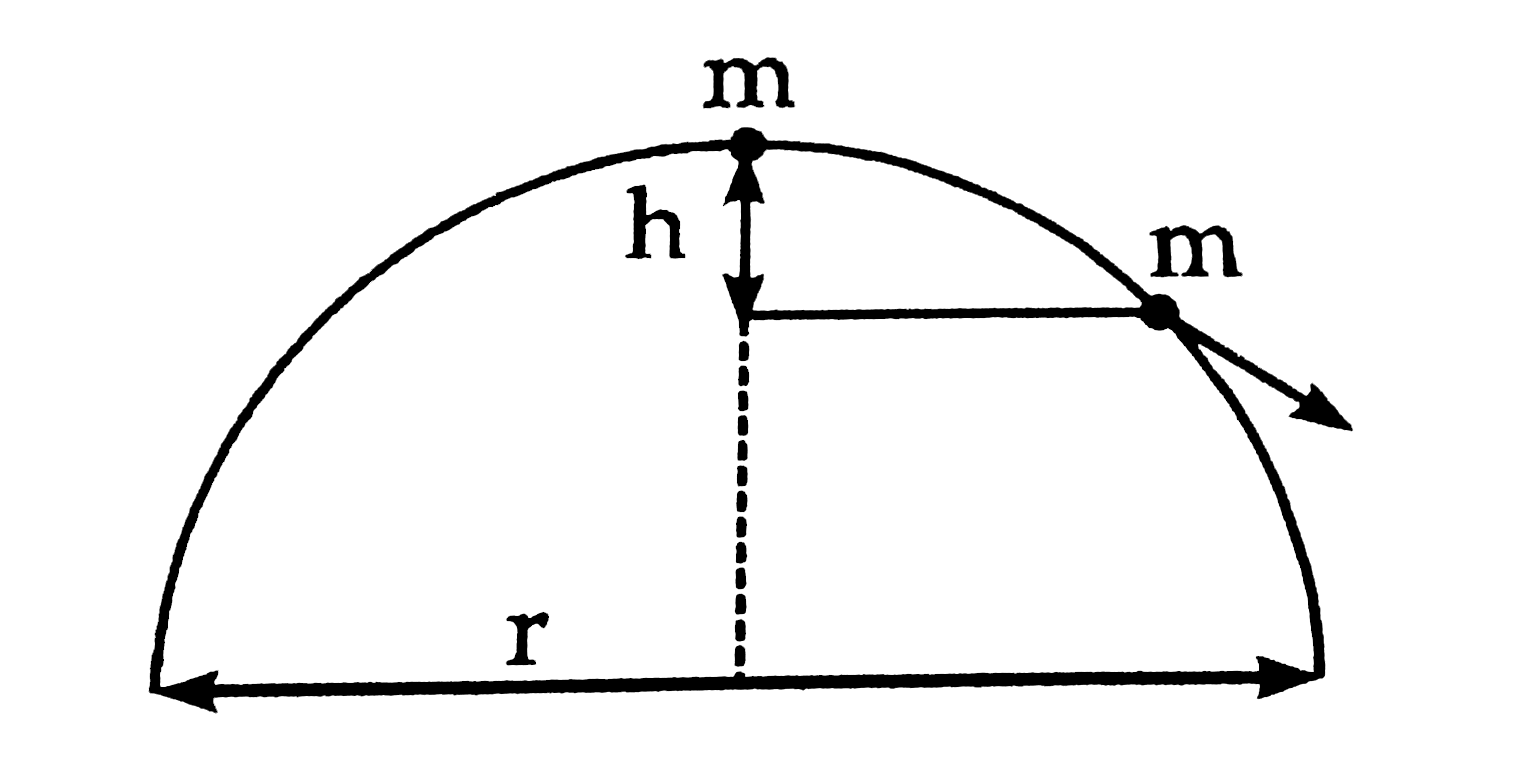
View Solution
Knowledge Check
A small body of mass m can slide without friction along a through bent which is in the form of a semi-circular arc of radius R. At what height h will the body be at rest with respect to the trough, if the trough rotates with uniform angular velocity ω about a vertical axis:
 ARBR−2gω2CR+2gω2DR−gω2
ARBR−2gω2CR+2gω2DR−gω2A small body of mass m slides without friction from the top of a hemisphere of radius r. At what height will the body be detached from the surface of hemisphere?
 A32rB23rC12gt2Dv22g
A32rB23rC12gt2Dv22gThe total surface area of a solid hemisphere of radius r is
Aπr2B2πr2C3πr2D4πr2
Determine the position of the centre of mass of a hemisphere of radius R.
View SolutionDetermine the centre of mass of a uniform hemisphere of radius R.
View SolutionA small block slides down from the top of hemisphere of radius R = 3 m as shown in the figure. The height 'h' at which the block will lose contact with the surface of the sphere is __________ m.
(Assume there is no friction between the block and the hemisphere)
View SolutionA small disc is on the top of a hemisphere of radius R. What is the smallest horizontal velocity v that should fbe given to the disc for it to leave the hemisphere and not slide down it?[There is no friction]
View SolutionA body of mass Mkg is on the top point of a smooth hemisphere of radius 5m . It is released to slide down the surface of hemisphere it leaves the surface when its velocity is 5ms−1 At this instant the angle made by the radius vector of the body with the vertical is ( Take g=10m/s2)
View Solution
