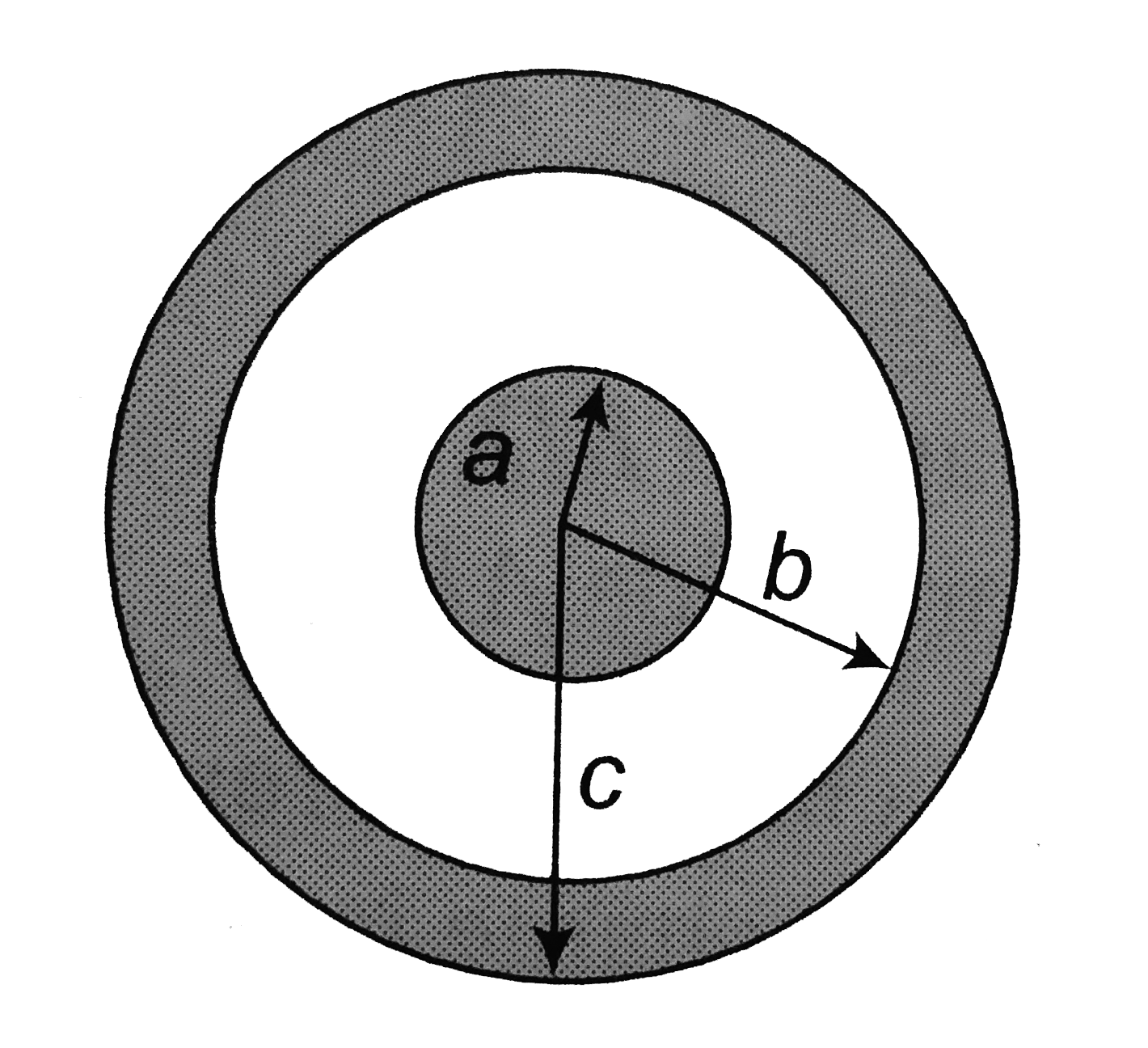
A small conducting sphere of radius a mounted on an insulated handle and a positive charge q is inserted through a hole in the wall of a hollow conducting sphere of inner radius b and outer radius c. The hollow sphere is supported on an insulating stand and is initially uncharged. The small sphere is placed at the center of the hollow sphere. Neglect any effect of the hole. Which of the following statements will be true for this system?
No work will be done in carrying a small charge from the inner conductor to the outer conductor.
The electric field at a point in the region between the spheres at a distance r from the center is equal to q/4πε0r2.
The electric field at a point outside the hollow sphere at a distance r from the centre is q/4πε0r2.
The potential of the inner sphere with respect to the outer sphere is given by Vab=q4πε0(1a−1b).
The correct Answer is:B, C, D
To solve the problem, we need to analyze the situation step by step, considering the properties of electric fields and potentials in conductors.
Step 1: Understand the System
We have a small conducting sphere of radius a with a positive charge q placed at the center of a hollow conducting sphere with inner radius b and outer radius c. The hollow sphere is initially uncharged and is insulated.
Step 2: Charge Induction
When the small charged sphere is placed at the center of the hollow conducting sphere, it induces charges on the inner surface of the hollow sphere. The inner surface will acquire a negative charge of −q due to the presence of the positive charge q at the center. Consequently, the outer surface of the hollow sphere will acquire a positive charge of +q to keep the entire hollow sphere neutral.
Step 3: Electric Field Inside the Hollow Sphere
To find the electric field at a point inside the hollow sphere (between the inner surface and the small sphere), we can apply Gauss's Law. The electric field E at a distance r from the center (where r<b) is given by:
E⋅4πr2=qϵ0
Thus, the electric field E inside the hollow sphere is:
E=q4πϵ0r2
This confirms that the electric field behaves as if all the charge q is concentrated at the center.
Step 4: Electric Field Outside the Hollow Sphere
For points outside the hollow sphere (at a distance r from the center where r>c), we again apply Gauss's Law. The total charge enclosed by a Gaussian surface outside the hollow sphere is q (the positive charge on the outer surface). Thus, the electric field E at a distance r from the center is:
E⋅4πr2=qϵ0
Therefore, the electric field outside the hollow sphere is:
E=q4πϵ0r2
Step 5: Potential Difference Between Inner and Outer Sphere
To find the potential difference between the inner sphere and the outer sphere, we calculate the potentials at both surfaces. The potential V1 at the inner surface (radius b) is influenced by the charge q and the induced charge −q:
V1=k(qa−qb)
The potential V2 at the outer surface (radius c) is:
V2=k(qc)
The potential difference V1−V2 gives us:
V1−V2=kq(1a−1b−1c)
Step 6: Work Done in Moving a Charge
The work done W in moving a small charge q′ from the inner to the outer conductor is given by:
W=q′ΔV
Since ΔV is not zero, work will be done in moving the charge.
Conclusion
Based on the analysis:
- Statement B: True, the electric field inside the hollow sphere is q4πϵ0r2.
- Statement C: True, the electric field outside the hollow sphere is also q4πϵ0r2.
- Statement D: True, the potential difference is given by kq(1a−1b−1c).
- Statement A: False, work will be done in moving a charge from the inner to the outer conductor.
We have a small conducting sphere of radius a with a positive charge q placed at the center of a hollow conducting sphere with inner radius b and outer radius c. The hollow sphere is initially uncharged and is insulated.
When the small charged sphere is placed at the center of the hollow conducting sphere, it induces charges on the inner surface of the hollow sphere. The inner surface will acquire a negative charge of −q due to the presence of the positive charge q at the center. Consequently, the outer surface of the hollow sphere will acquire a positive charge of +q to keep the entire hollow sphere neutral.
To find the electric field at a point inside the hollow sphere (between the inner surface and the small sphere), we can apply Gauss's Law. The electric field E at a distance r from the center (where r<b) is given by:
E⋅4πr2=qϵ0
Thus, the electric field E inside the hollow sphere is:
E=q4πϵ0r2
This confirms that the electric field behaves as if all the charge q is concentrated at the center.
For points outside the hollow sphere (at a distance r from the center where r>c), we again apply Gauss's Law. The total charge enclosed by a Gaussian surface outside the hollow sphere is q (the positive charge on the outer surface). Thus, the electric field E at a distance r from the center is:
E⋅4πr2=qϵ0
Therefore, the electric field outside the hollow sphere is:
E=q4πϵ0r2
To find the potential difference between the inner sphere and the outer sphere, we calculate the potentials at both surfaces. The potential V1 at the inner surface (radius b) is influenced by the charge q and the induced charge −q:
V1=k(qa−qb)
The potential V2 at the outer surface (radius c) is:
V2=k(qc)
The potential difference V1−V2 gives us:
V1−V2=kq(1a−1b−1c)
The work done W in moving a small charge q′ from the inner to the outer conductor is given by:
W=q′ΔV
Since ΔV is not zero, work will be done in moving the charge.
Based on the analysis:
- Statement B: True, the electric field inside the hollow sphere is q4πϵ0r2.
- Statement C: True, the electric field outside the hollow sphere is also q4πϵ0r2.
- Statement D: True, the potential difference is given by kq(1a−1b−1c).
- Statement A: False, work will be done in moving a charge from the inner to the outer conductor.
Similar Questions
A hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
 View Solution
View SolutionA conducting sphere of radius r has a charge . Then .
View SolutionIf a solid and a hollow conducting sphere have same radius then
View SolutionSelf energy of conducting sphere of radius .r. carrying charge .Q. is ______
View SolutionA solid conducting sphere of radius a has a net positive charge 2Q. A conducting spherical shell of inner radius b and outer radius c is concentric with the solid sphere and has a net charge −Q. The surface charge density on the inner and outer surfaces of the spherical shell will be
 View Solution
View SolutionA small conducting sphere is hanged by an insulating thread between the plates of a parallel plate capacitor as shown in figure. The net force on the sphere is
View SolutionThe moment of inertia of hollow sphere (mass M) of inner radius R and outer radius 2R, having material of uniform density, about a diametric axis is
View SolutionA point charge q is placed at a distance of r from cebtre of an uncharged conducting sphere of rad R(<r). The potential at any point on the sphere is
View SolutionAcidified water from certain reservoir kept at a potential V falls in the form of small droplets each of radius r through a hole into a hollow conducting sphere of radius a. The sphere is insulated and is initially at zero potential. If the drops continue to fall untill the sphere is half full, the potential acquired by the sphere is
View SolutionA solid, uncharged conducting sphere of radius 3a contains a concentric hollowed spherical cavitiy of radius a.
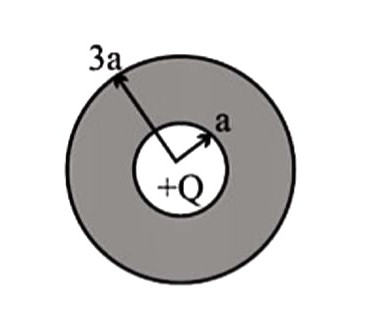
A point charge +Q is placed at the center of the spheres. Taking V=0 at r→∞, the potential at positiion r=2a from the center is-View Solution
