A small glass sphere of radius 2x10−3mis moving through a liquid of viscosity 0.11 decapaise. Calculate the viscos force acting on it if the speed of the ball is 0.05ms−1
The correct Answer is:0.21×10−3N
To calculate the viscous force acting on a small glass sphere moving through a liquid, we can use the formula for viscous force, which is given by:
F=6πηrv
Where:
- F is the viscous force,
- η is the viscosity of the liquid,
- r is the radius of the sphere,
- v is the speed of the sphere.
Step 1: Convert viscosity from decapoise to Pascal-seconds
The viscosity is given as 0.11 decapoise. We need to convert this to Pascal-seconds (Pa·s) since 1 decapoise = 1 Pa·s.
η=0.11decapoise=0.11Pa⋅s
Step 2: Identify the values
- Radius r=2×10−3m
- Speed v=0.05m/s
- Viscosity η=0.11Pa⋅s
Step 3: Substitute the values into the formula
Now we can substitute these values into the viscous force formula:
F=6π(0.11)(2×10−3)(0.05)
Step 4: Calculate the force
Calculating the values step by step:
1. Calculate 6π:
6π≈6×3.14≈18.84
2. Multiply by the viscosity:
18.84×0.11≈2.0724
3. Multiply by the radius:
2.0724×(2×10−3)≈0.0041448
4. Finally, multiply by the speed:
0.0041448×0.05≈0.00020724N
Step 5: Express in scientific notation
F≈0.21×10−3N=2.1×10−4N
Final Answer
The viscous force acting on the sphere is approximately 0.21×10−3N.
---
- F is the viscous force,
- η is the viscosity of the liquid,
- r is the radius of the sphere,
- v is the speed of the sphere.
The viscosity is given as 0.11 decapoise. We need to convert this to Pascal-seconds (Pa·s) since 1 decapoise = 1 Pa·s.
- Radius r=2×10−3m
- Speed v=0.05m/s
- Viscosity η=0.11Pa⋅s
Now we can substitute these values into the viscous force formula:
Calculating the values step by step:
6π≈6×3.14≈18.84
18.84×0.11≈2.0724
2.0724×(2×10−3)≈0.0041448
0.0041448×0.05≈0.00020724N
F≈0.21×10−3N=2.1×10−4N
The viscous force acting on the sphere is approximately 0.21×10−3N.
Topper's Solved these Questions
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS ( FROM PRESSURE, ARCHIMEDES. PRINCIPLE)
7 Videos
- INTERNAL ENERGY BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM HEAT ENGINES)
21 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
Similar Questions
A raindrop of radius 0.2 mm falls through air: If the viscosity of air is 18 ×10−6 Pl, find the viscous drag acting on the drop when its speed is 1 m s−1.
View SolutionA steel ball of radius 2×10−3m is released in an oil of viscosity 0.232Nsm−2 and density 840kgm−3. Calculate the terminal velocity of ball. Take density of steel as 7800kgm−3
View Solution
Knowledge Check
A rain drop of radius 0.3 mm falls through air with a terminal viscosity of 1ms−1. The viscosity of air is 18×10−5 poise. The viscous force on the rain drop is
A1.018×10−2 dyneB2.018×10−2 dyneC3.018×10−2 dyneD4.018×10−2 dyne
A metal plate 0.04m2 in area is lying on a liquid layer of thickness 10−3m and coefficient of viscosity 140 poise. Calculate the horizontal force needed to move the plate with a speed of 0.040 m/s.
View SolutionAn air bubble of 1cm radius is rising at a steady rate of 0.5cms−1 through a liquid of density 0.81gcm−3. Calculate the coefficient of viscosity of the liquid. Neglect the density of air. ( Take g=10m/s2)
View SolutionA small metal sphere of radius a is falling with a velocity υ through a vertical column of a viscous liquid. If the coefficient of viscosity of the liquid is η, then the sphere encounters an opposing force of
View SolutionAn air bubble of radius 10−2 m is rising up at a steady rate of 2×10−3ms−1 through a liquid of density 1.5×103kgm−3 , the coefficient of viscosity neglecting the the density of air, will be (g=10ms−2)
View SolutionCalculate the de Broglie wavelength of a ball of mass 0.1kg moving with a speed of 30ms−1
View SolutionA uniformly tapering vessel is filled with a liquid of density 900km/m3. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)
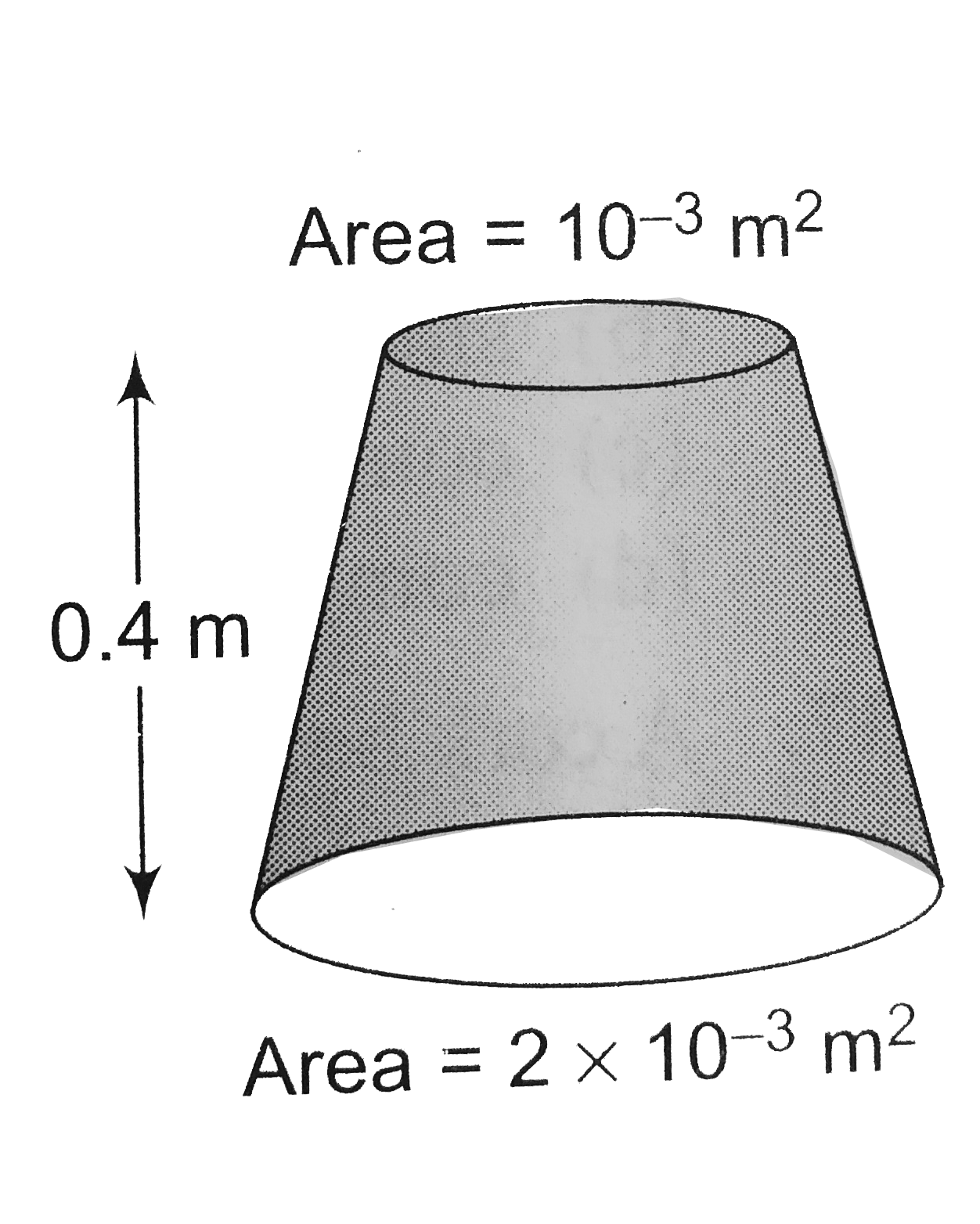
View SolutionA small steel ball of radius r is allowed to fall under gravity through a column of a viscous liquid of coefficient of viscosity η. After some time the velocity of the ball attains a constant value known as terminal velocity υT. The terminal velocity depends on (i) the mass of the ball m (ii) η, (iii) r and (iv) acceleration due to gravity g . Which of the following relations is dimensionally correct?
View Solution
